Осевые, центробежный и полярный моменты инерции. Понятие о радиусах инерции и моментах сопротивления
Интегралы вида
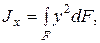
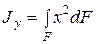, (2.5)
называются осевыми моментами инерции относительно осей х и у. Их значения всегда положительные.
Интеграл вида:
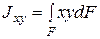(2.6)
называется центробежным моментом инерции. Он может принимать разные знаки и может быть равным нулю. Оси, относительно которых центробежный момент инерции равен нулю, называются главными осями. А если они проходят ещё и через центр тяжести сечения, то они будут главными центральными осями. Таким образом, основной задачей данного раздела сопротивления является материалов приобрести навык при вычислении осевых моментов инерции относительно главных центральных осей.
И далее, интеграл вида:
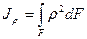(2.7)
описывает полярный момент инерции. Из (рис. 2.1) следует, что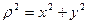 
. Тогда полярный момент инерции
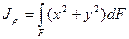или 
, 
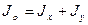(2.8)
т.е. полярный момент инерции, заданного сечения равен сумме осевых моментов инерции.
В частном случае для круглого сечения
; 
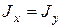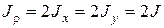(2.9)
Приведенные осевые моменты инерции применяют при вычислении осевых радиусов инерции
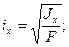
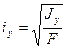(2.10)
Отношение осевых моментов инерции Jx, Jy к координатам наиболее удаленных точек по осям уmax и хmax называется осевыми моментами сопротивления, т.е:
|
|
|
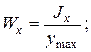
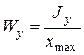, (2.11)
где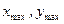 
- координаты наиболее удаленных точек в системе главных центральных осей.
Все эти геометрические характеристики будут использованы при выводе всех расчетных формул сопротивления материалов по оценке прочности, жесткости и устойчивости элементов конструкций.
Зависимость между моментами инерции при параллельном переносе осей
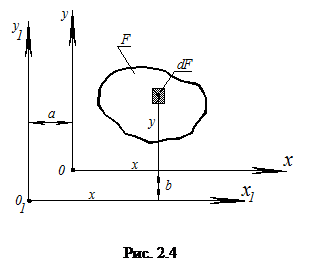
Пусть известны значения статических моментов площади и моментов инерции, определяемых формулами (2.2), (2.5), (2.6) относительно осей х и у. Требуется определить значения моментов инерции относительно другой системы осе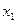й 
и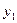 
, которые параллельны осям х и у (рис. 2.4). Для новых осей можно записать:
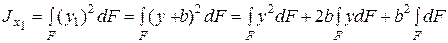
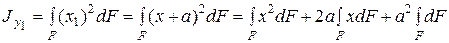
С учетом зависимостей (2.2), (2.5), (2.6) последние равенства можно переписать так:
;
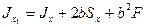(2.12)
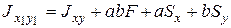
Последние формулы справедливы для случайных осей х и у. Если же исходные оси х и у центральные, то статические моменты площади сечения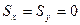 
. С учетом этого окончательно получим:
;
;
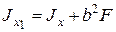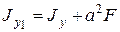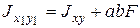. (2.13)
|
|
|
Формулы (2.13) показывают, что по мере удаления от центра тяжести моменты инерции возрастают и, наоборот, по мере приближения к центральным осям моменты инерции убывают.
Моменты инерции простейших сечений
Для простейших сечений моменты инерции определяют методом непосредственного интегрирования. Рассмотрим некоторые примеры решения задач по определению моментов инерции простейших фигур:
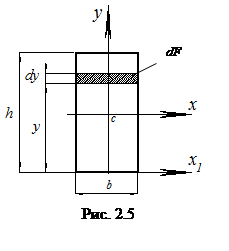а) Прямоугольник с размерами b 
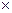h (рис. 2.5). Для решения задачи воспользуемся формулами (2.5). Выберем вспомогательную ось 
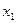. На расстоянии у от оси х1 выделим элементарную площадку dF=bdy. Подставляя площадь элементарной площадки dF в формулу (2.5), определим осевой момент инерции относительно оси х1:
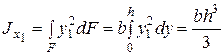
Теперь найдем момент инерции относительно оси х, применяя первую из формул (2.13):
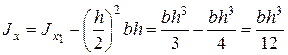(2.14)
Аналогично можно найти осевой момент инерции относительно оси у:
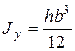
б) Треугольник с основанием b, высотой h (рис. 2.3). Выделенную элементарную площадь dF подставим в формулу (2.5). Получаем значение момента инерции относительно оси х1:
.
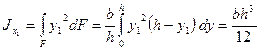Момент инерции относительно оси х, параллельной данной оси х1, найдем по первой формуле (2.13):
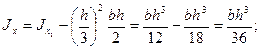
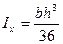(2.14*)
|
|
|
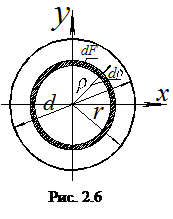
в) Круградиусом r (диаметром d) (рис. 2.6). Найдем сначала полярный (2.7) момент инерции по формуле:
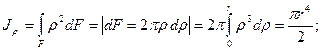
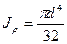(2.15)
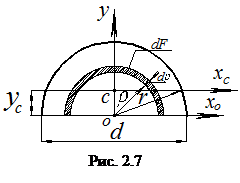г) Полукруг радиусом r =d/2 (рис.2.7). Приведем без вывода формулы для определения координаты центра тяжести ус полукруга и вычисления моментов инерции относительно главных центральных осей х и у
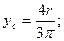
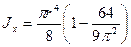; (2.16)
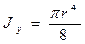
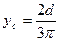
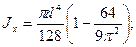(2.17)
;
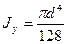Обучающемуся рекомендуется получить приведенные ответы решений самостоятельно, пользуясь (рис. 2.7).
Дата добавления: 2018-11-24; просмотров: 410; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!