МАТЕМАТИЧЕСКИЕ ОСНОВЫ РАЗРАБОТКИ И ОПТИМИЗАЦИИ ПРОЕКТА ШАХТЫ.

⇐ ПредыдущаяСтр 3 из 5Следующая ⇒

Математическая сущность горных задач. Классические методы оптимизации проектных решений. Метод расчетных вариантов, методы теории принятия сложных решений, методы неопределенных множителей Лагранжа и градиентов. Особенности методов, преимущества и недостатки, область применения.

Методы математического программирования: линейного, нелинейного и динамического. Сущность, особенности, преимущества и недостатки, область применения.

Литература: [2, с.112-142],

[ 1, с.91-154, 212-272, 356-376],

[ 4, с. 284-309].

Методические указания.

При освоении данной темы студент должен знать, что математическая сущность горных задач заключается в применении всех существующих математических методов, дающих определение интересующего нас объекта (задачи), выбора переменных, характеризующих объект или описывающих его поведение.

Необходимо знать сущность классических методов оптимизации проектных решений, нашедших применение в горном деле, их достоинства и недостатки, область применения каждого из методов и с их помощью уметь решать горные задачи. К таким методам относятся: статистический, аналитический, графоаналитический, графический, метод вариантов и др.

Из перечисленных методов студент должен знать и уметь применять следующие:

1. Статистический метод. Сущность данного метода заключается в том, что для установления влияния какого-либо фактора (например, длины лавы на стоимость 1 т угля, производственной мощности, производительности труда и др.) собираются данные по большому числу объектов и обрабатываются методами математической статистики. Обработка производится в следующей последовательности:

– строится график влияния переменной величины на искомый параметр;

– устанавливается вид зависимости (формула);

– проверяется правильность выбранной зависимости;

– определяются коэффициенты, входящие в найденную формулу.

Необходимо знать правила построения графиков, уметь подбирать по виду кривой формулу, выражающую статическую зависимость, и проверить правильность ее выбора, определять коэффициенты методом наименьших квадратов и графоаналитическим способом.

2. Аналитический метод. Сущность его заключается в том, что в математическом виде записываются затраты (или используется другой критерий) в функции от искомого параметра, после чего находится его минимальное или максимальное значение путем взятия первой производной и приравнивания ее к нулю.

Например, при оптимизации одного из параметров функция будет иметь вид

f ( x ) = ,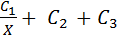

где С₁ , С₂ ,С₃ – стоимостные коэффициенты.

Как видно из выражения, функция имеет экстремум, так как с изменением значения Х одни затраты будут возрастать, другие уменьшаться, а третьи остаются без изменений. Чтобы найти оптимальное значение по Х, надо взять первую производную и приравнять ее к нулю:

f^/ ( x ) = 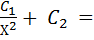0, Х_ОП = .

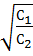3. Графический метод. Он используется как вспомогательный. Например, при решении горных задач аналитическим методом, когда полученные уравнения являются функцией двух переменных и решение их обычными методами затруднительно, тогда целесообразно применять графический метод.

4. Метод вариантов. С помощью этого метода можно решать практически любые задачи горного дела с одновременным нахождением большого количества неизвестных величин, то есть решать глобальные задачи с установлением оптимальных значений все основных параметров шахты. Например, записав в математическом виде все затраты на 1 т добываемого угля в функции от основных параметров (производственной мощности, размеров шахтного поля, длины и разгрузки на лаву, схему вскрытия и подготовки и др.) и, найдя минимум этой функции, мы определим оптимальные значения одновременно всех этих параметров. Минимум затрат определяется путем вычисления значений критерия оптимальности по отдельным вариантам при различных значениях переменных величин и сравнения результатов вычислений между собой.

Такие задачи рационально решать на ЭВМ. При этом машина не только выбирает различные числовые значения переменных, но и компонует сами технологические решения, используя шкалу вариантов. Это так называемый метод полного перебора вариантов.

Сущность его заключается в том, что для большого количества технологических решений проводятся детальные расчеты величины затрат или других критериев при различных значениях основных параметров с последующим сравнением и выбором наилучшего варианта.

По вопросу теории принятия сложных решений необходимо знать сущность и область применения данной теории в горном деле. Методы теории принятия сложных решений (метод предпочтения, метод ранга, метод весовых оценок и метод нормы вектора) рассмотрены в пятом разделе при интегральной оценке качества проектных решений. В данном вопросе необходимо изучить метод экспертных оценок и заданных отклонений.

Применение методов неопределенных множителей Лагранжа и градиентов, применительно к горным задачам, удобнее всего рассмотреть на примере оптимизации площадей сечения горных выработок и распределения депрессии.

I . Метод градиентов. По существу метод градиентов представляет собой метод покоординатного спуска целевой функции по многим переменным. В нашем примере в качестве переменных выступают площади сечения горных выработок. Математически метод градиентов можно выразить как частную производную целевой функции по неизвестному переменному.

Порядок определения оптимальных сечений горных выработок методом градиентов следующий:

1. Сеть выработок шахты расчленяется на отдельные направления (цепи), представляя, что они определяют депрессию шахты (рис. 6.1).

Площади сечения выработок определяются из расчета, что стоимостная функцияпо площади сечения f ( F_i ) будет минимальной

С = f ( F_i ) = ∑ К _i + ∑ r_i → min

где ∑ К _i– суммарная стоимость 1 м² проведения выработок, руб.;

∑ r_i – стоимость поддержания 1 м² выработок, руб.

Кроме того, необходимо выдержать условие, что депрессия цепиh должна быть равной допустимой h_доп, а увеличение сечения выработки давало минимальный прирост стоимостной функции С.

2. Устанавливаются минимально допустимые площади сечения каждой выработки по цепи F _min и назначается, так называемый нулевой шаг (см. рис. 6.1). Для каждой выработки устанавливается сумма затрат на перекрепление С _min .

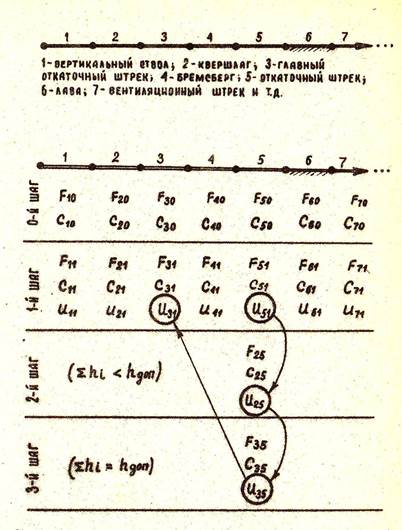
Рис. 6.1. Схема пошагового решения задачи методом градиентов

3. Назначается шаг изменения площади сечения выработок ∆ F – в любом диапазоне (0,2 м² , 0,5 м² , 1,0 м² , и т.д.). Таким образом, возникают новые площади сечения F₁₁ и соответственно новые их стоимости С₁₁ – то есть устанавливается новый шаг – 1-й шаг.

4. По каждой выработке принимаем критерий перехода U _i от однойвыработки к другой из-за изменения депрессии ∆ h_i и стоимости ∆С _i при увеличении площади сечения на ∆F _i, который равен

U_i = 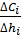→ min .

5. По критерию перехода – U устанавливаем выработку с минимальным сечением (то есть при минимальном значении U).

Это необходимо для того чтобы не увеличивать сечение выработки всей цепи, а только единичной – с F _min . Например, это выработка №5 по принятой схеме.

6. Назначается новый (2-й шаг) и снова определяется выработка с минимальным сечением по критерию перехода U , которая и принимается к увеличению площади сечения (по сравнению с предыдущим шагом).

Такой перебор выработок по шагам производят до тех пор, пока сумма депрессий ∑ h_i , выработок не будет равна допустимой депрессии – h_доп.

Смысл вектора-градиента заключается в том, что при бесконечно малом шаге изменения площади сечения выработок отношение ∆ C_i / ∆ h_i есть не что иное, как частная производная стоимостной функции по площади сечения выработок (то есть неизвестному).

II . Метод определения множителей Лагранжа. Сущность метода состоит в том, что и для решения задачи методом градиентов - при увеличении площади сечения выработок будет расти их стоимость и снижаться величина депрессии.

Таким образом, систематизируется единая целевая функция, которая объединяет две разные по смыслу функции, а именно:

– стоимостная – С = f ( F_i );

– депрессионная – ∑ h_i = f ( F_i ).

С целью объединения этих двух функций разного смысла и вводится неопределенный множитель Лагранжа – λ.

Общая целевая функция будет иметь вид

L = f ( F_i) + λ φ_i (h_i) → min .

Порядок определения оптимальных сечений горных выработок данным методом следующий:

1. Определяется неопределенный множитель Лагранжа

λ = ( 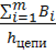)^1,4 ,

где m – количество выработок в цепи;

h _цепи – депрессия цепи;

B_i – вентиляционно-стоимостная характеристика выработки, выражение которой имеет следующий вид:

B_i = l_i ,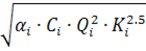

где l_i– длина i-той выработки, м;

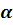_i – коэффициент аэродинамического сопротивления i-той выработки, кгс 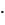с² /м⁴;

С _i– коэффициент, учитывающий форму сечения выработки (принимается от 3,54 до 4,15);

Q_i– количество проходящего воздуха по i-той выработке, м³/с;

K_i – условный коэффициент важности i-той выработки(принимается от 0 до 1).

2. Определяется оптимальная площадь сечения i-той выработки, которая учитывает обе выше приведенных функций:

F_i = .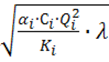

3. Определяется депрессия для рассматриваемой i-той выработки:

h_i = 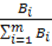h_ц .

Окончательный выбор площади сечения горной выработки рекомендуется проводить по типовым сечениям – ближайших к расчетным.

Приступив к изучению методов математического программирования студент обязан знать (как было отмечено ранее), что большинство горных задач по своей природе являются многовариантными с большим числом переменных. Обычно классические методы, за исключением метода вариантов, для решения таких задач непригодны. Их решение стало возможным после внедрения методов математического программирования на ЭВМ. Это методы линейного, нелинейного, динамического программирования, метод графов и др.

Сущность их заключается в направленном переборе вариантов, позволяющем путем применения специального математического аппарата получить оптимальное решение без необходимости просчета всех возможных вариантов. Эти методы позволяют решать задачи не путем одноразовых вычислений, а методом последовательных приближений к наивыгоднейшему результату.

Методы линейного программирования широко используются для решения задач по оптимизации, выраженных системами линейных уравнений и неравенств.

Задача может быть сформулирована следующим образом: требуется определить максимальное или минимальное значение линейной функции многих переменных, принимающих только положительные значения и удовлетворяющих некоторым ограничениям, выраженных при помощи линейных уравнений или неравенств.

Примером может служить задача определения оптимальных размеров добычи на месяц по каждому очистному забою Х из условия, что общешахтная себестоимость добычи угля будут минимальной при выполнении плана добычи по шахте и соблюдения нормативных показателей качества угля, а также возможности каждого забоя.

Студент обязан уметь записать задачу линейного программирования в математическом виде:

С₁Х₁ + С₂Х₂ + … + С _i X_i + … + C_pX_p → min ( max ),

X₁ +X₂ +… + X_i +… + X_p ≥ A,

b₁₁ x₁ + b₁₂x₂ + … +b_1i x_i + …+ b_ipx_p≤ B₁,

………………………………………………………

b_g x₁ + b_g2x₂ + … +b_gi x_i + …+ b_gpx_p≤ B_g,

x ₁ ≥ 0; x ₂ ≥ 0; x_i ≥0; x_p ≥ 0

или в сокращенном виде:

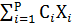→ min ( max ),

≥ A,

∑b_jix_i ≤ B_j;x_i ≥ 0 j = 1;2;3…g,

j =1;2;3… p

где С _i – стоимостной или другой показатель на i-м предприятии;

Х _i – количество выпускаемой продукциина i-м предприятии;

b_ig– затраты g-того вида фондируемого ресурса на i-м предприятии;

В _g– общие выделенные лимиты различных ресурсов.

Для данного вида задач характерны следующие особенности:

1.Математическая формулировка задачи содержит p неизвестных, а система состоит из 2 + p + g уравнений и неравенств, имеющих различный экономический смысл;

2. Число ограничений выбирается, исходя из сущности решаемой задачи;

3. Все равенства и неравенства, в том числе и сама функция, должны быть линейными.

При изучении данного курса студент должен овладетьдвумя методами решения задач линейного программирования – графическим и симплекс-методом.

1.Графический метод. Это один из самых простых, но позволяет решать задачи, содержащие не более 3-х переменных. Достоинство его, главным образом в том, что он позволяет понять и представить смысл всех методов линейного программирования.

Сущность графического метода заключается в том, что согласно общим правилам построения аналитических зависимостей, в системе координат X ₁ OX ₂ или X ₁ OX ₂ X ₃изображаются все неравенства, выражающие ограничения. Все точки полученного многоугольника или многогранника удовлетворяют условиям ограничения, но нас интересует такая точка, которая удовлетворяла бы и целевую функцию. Для нахождения ее необходимо совместно решить целевую функцию с многоугольником ограничений. Это будет какая-то крайняя точка или вершина многоугольника или многогранника.

Следует отметить, что и вообще решение задач линейного программирования любым методом сводится к отысканию таких вершин воображаемого многогранника, удовлетворяющего всем ограничениям, при которых целевая функция достигает минимума или максимума.

2. Симплекс-метод – универсальный метод, позволяющий практически решать любые задачи линейного программирования. Сущность его заключается в том, что в начале подбирается наиболее очевидная система значений переменных, удовлетворяющих всем ограничениям, но не обращающих целевую функцию в минимум или максимум (так называемый опорный план или решение), а затем путем выполнения ряда последовательных математических операций приближаются к оптимальному результату.

Все расчеты симплекс-метода при ручном счете выполняются в таблицах по определенному алгоритму, который используется и в ЭВМ. Алгоритм этого метода студент должен четко усвоить. Он заключается в следующем:

1. Записывается система ограничений

y_i = - a_i1x₁- a_i2x₂ - … - a_inx_n + B_i ≥ 0, i = 1; 2 … m.

2. Система преобразованных ограничений и линейная функция записывается в виде таблицы, называемой – исходная симплекс-таблица.

	- x₁	- x₂	…	- x_n	1
y₁	a₁₁	a₁₂	…	a_1m	B₁
…	…	…	…	…	…
y_m	a_m1	a_m2	…	a_mn	B_n
z	- p₁	- p₂	…	- p_n	0

3. Приступают к анализу полученной таблицы, и в первую очередь столбца свободных членов. Здесь может быть два случая:

а) все свободные члены положительные. В этом случае таблица сразу дает опорное решение системы ограничений. Значения линейной функции в этом случае равно 0 (план «бездеятельности» при оптимизации плана выпуска продукции предприятиями);

б) в столбце свободных членов имеются отрицательные элементы. В этом случае для отыскания опорного решения необходимо произвести один или несколько шагов модифицированных жордановых исключений, пока не будет достигнута положительность все членов столбца.

Оптимальное решение при максимизации целевой функции достигается в том случае, если в ее строке z oтсутствуют коэффициенты с отрицательными знаками, при минимизации – если отсутствуют коэффициенты с положительными знаками. В противном случае необходимо произвести один или несколько шагов модифицированных жордановых исключений с разрешающим элементом.

Динамическое программирование представляет собой метод, позволяющий решать задачи по выбору оптимального решения независимо от характера целевой функции.

Студент должен уяснить, что основу метода составляет замена задачи одной функции со многими переменными задачей многих функций с одной переменной, так как одномерные задачи более просты и легче поддаются решению.

Следует обратить внимание на особенность задач динамического программирования, заключающуюся в том, что при их решении необходимо учитывать фактор времени или последовательности операций. Чаще всего это рациональное распределение имеющихся в нашем распоряжении ограниченных ресурсов.

Применительно к горному производству можно назвать ряд таких задач, которые решаются методом динамического программирования. Это: оптимальное распределение капитальных вложений между строящимися или реконструируемыми шахтами; определение оптимальных скоростей проведения горных выработок; решение задач календарного планирования и др.

Студенту рекомендуется на основе изучения метода дополнить перечень горных задач.

Вопросы для самопроверки.

1. Математическая сущность горных задач.

2. Методы оптимизации проектных решений.

3. Сущность статистического метода.

4. Сущность аналитического метода.

5. Сущность графического метода.

6. Сущность метода вариантов.

7. Достоинства и недостатки, область применения расчетных методов.

8. Сущность и применение метода градиентов.

9. Сущность и применение метода неопределенных множителей Лагранжа.

10. Общая постановка горной задачи для решения методам линейного программирования.

11. Модель задачи линейного программирования.

12. Графический метод решения задач линейного программирования.

13. Сущность симплекс-метода.

14. Алгоритм преобразования симплекс-матрицы при достижении опорного решения задачи линейного программирования.

15. Алгоритм преобразования симплекс-матрицы при достижении оптимального решения задачи линейного программирования.

16. Общая постановка горной задачи для решения методом динамического программирования.

17. Возможные этапы и алгоритм решения задачи методом динамического программирования.

18. Понятия условно-оптимального эффекта на каждом этапе и связь их по этапам при решении задачи динамического программирования.

Дата добавления: 2018-11-24; просмотров: 234; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 234 5 Следующая ⇒

Мы поможем в написании ваших работ!