Сумма ряда. Примеры сходящихся и расходящихся рядов. Гармонический ряд (док-во его расходимости)
Сумма вида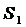 
= 
= 
+ 
= 
+ 
= + 
+… 
= 
+ 
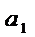
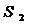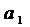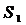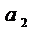
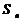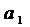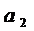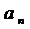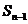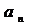
Называется частичными суммами ряда 1,
а последовательность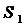 
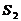
(2) называется последовательность частичных сумм ряда (1)
Ряд (1) наз сход,если сх-ся посл-ть его частичных сумм(2)
т.е если 
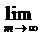
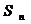=S При этом число S называется суммой ряда (1)
А если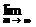 
= 
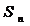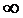или не сущ то ряд (1) наз расход.
Примеры рядов:
• 
расходится
• 
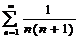сходится
Ряд вида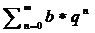 
- геом.прогрессия,рядсход.если 
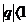и его сумма S=b/1-q,если 
ряд расх.
Свойства сходящихся рядов
Свойства-1. Если ряд u1+u2+u3+….un+…=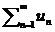 
(1) сход(расх.). И его сумма-S то сход(расх если с не равно 0) ,также и ряд 
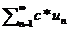и его сумма c*S.
2.Если ряд (1) и ряд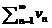 
их суммы S1 и S2 соответственно ,то сход и ряды 
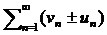и их суммы равны S1+S2.
3.Если к ряду (1) прибавить или отнять от него конечное число членов, то получим ряд и ряд (1) сход или расх одновременно. Ряд un+1+un+2+…=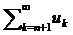 
обознач. Rn-остаток ряда (1),если ряд (1) сход. то его остаток стрем.к 0 при n стрем. к бесконечн.( 
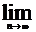Rn=0).
Необход.признак сходимости- если ряд(1) сход. то общий член этого ряда стрем к 0 (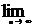 
an=0) Док-во: 
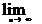un=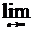 
(Sn-Sn-1)=0. Данный признак –не явл-ся достаточным(например гарм. ряд расх но un= 1/n стрем. к 0).
Док-ворасх-ти гармонического ряда по Коши: f(x)=1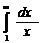/x 
= 
; 
= 
(lnx)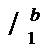 
= 
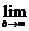(lnB*0),где lnB→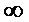 
Ряд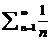 
гармонический и он всегда расход
Так называется ряд (бесконечная сумма), члены которого образуют геометрическую прогрессию с первым членом а0 и знаменателем прогрессии, равным q.
|
|
|
Если |q| < 1, то существует предел суммы n первых членов этой прогрессии при неограниченном увеличении количества этих членов n:
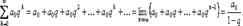
Признак сравнения рядов с положительными членами
1-й признак сравнения:
Пусть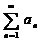 
(1) и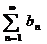 
(2) с неотриц членами. Тогда если вып-сянер-во 
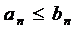начиная с некотn, то если ряд 2 сх-ся, то и ряд 1 сх-ся, а если ряд 1 расх-ся, то и ряд 2 расх-ся.
2-й признак сравнения:
Пусть заданы ряд (1) и (2), члены кот положит и сущ 
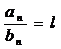, 0<l<∞. Тогда эти ряды (1), (2) одновр-но сх-ся или расх-ся
28.Достат признаки сх-ти ряда сположит членами.
Признак Даламбера:
Пусть задан ряд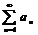 
и сущ 
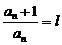, тогда
если l<1, ряд сх-ся
l>1, ряд расх-ся
l=1, ?
Признак Коши: Пусть задан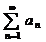 
и сущ 
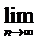
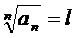, тогда если
l<1, ряд сх-ся
l>1, ряд расх-ся
l=1, ?
1-й признак сравнения:
Пусть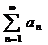 
(1) и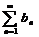 
(2) с неотриц членами. Тогда если вып-сянер-во 
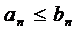начиная с некотn, то если ряд 2 сх-ся, то и ряд 1 сх-ся, а если ряд 1 расх-ся, то и ряд 2 расх-ся.
2-й признак сравнения:
Пусть заданы ряд (1) и (2), члены кот положит и сущ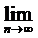 
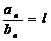, 0<l<∞. Тогда эти ряды (1), (2) одновр-но сх-ся или расх-ся
Интегральный признак сходимости ряда с положительными членами.
Пусть задан ряд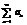 
, члены кот положит и не возр-т, т.е. 
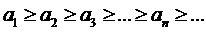, а ф-я f(x) непрер, невозраст на [1;∞) f(1)=a1, f(2)=a2…f(n)=an
|
|
|
Тогда если 
сх-ся, то и числовой ряд сходится и наоборот.
Обобщенным гармоническим рядом (или рядом Дирихле) называют ряд
.
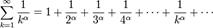Обобщенный гармонический ряд расходится при α≤1 и сходится при α>1
Знакопеременные ряды. Абсолютная и условная сходимость.
Числовой ряд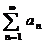 
, содержащий бесконечное множество положительных и бесконечное множество отрицательных членов, наз-сязнакопеременным.
Если ряд, сост из абсол значений величин 
сх-ся, то ряд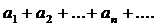 
наз абсолютно сходящимся.
Дата добавления: 2018-04-05; просмотров: 513; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!