Определенный интеграл с переменным верхним пределом
Ф-я вида 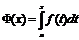 , где x
, где x  наз интегралом cперем верхним пределом. Т: Если
наз интегралом cперем верхним пределом. Т: Если  непрер на
непрер на  , то произв-я ф-и
, то произв-я ф-и 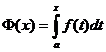 ,сущ в каждой точке
,сущ в каждой точке 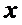 на
на 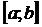 , причем
, причем 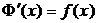
Интегрирование по частям и замена переменной в определенном интеграле
Формула интегрирования по частям для определенном интеграла.
Пусть заданны  тогда имеет место интегрирование по частям:
тогда имеет место интегрирование по частям:
 →
→ 
Замена переменной в определенном интеграле.
Пусть 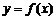 непрерывна на
непрерывна на 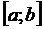 , а
, а  непрерывна на
непрерывна на 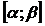 . Вместе со своей производной
. Вместе со своей производной 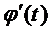 ; причем
; причем 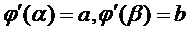 , и сложная функция
, и сложная функция  непрерывна на
непрерывна на 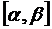 , тогда справедливо формула замены переменной для определенного интеграла:
, тогда справедливо формула замены переменной для определенного интеграла: 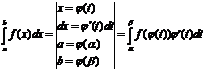
Геометрич приложения определенного интеграла
Вычисление площадей плоских фигур:
 1.
1. 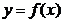 на
на 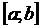 и
и 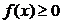
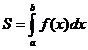
 2.
2.  на
на  и
и 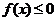
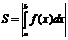
 3.
3. 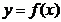 на
на 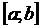 график имеет вид
график имеет вид
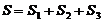
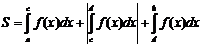
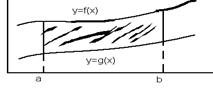 4. даны две функции:
4. даны две функции: 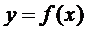 и
и 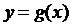 на промежутке
на промежутке 

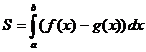
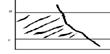 5.
5.  на промежутке
на промежутке  то получаем
то получаем 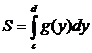
 6.
6. 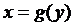 и
и 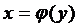 на промежутке
на промежутке 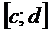 (графики ориентированнына
(графики ориентированнына 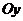 )
) 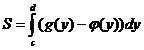
А
7.вычисление площади плоской фигуры заданной системе координат. В полярной системе точка это пара чисел 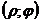 , любая линия равна
, любая линия равна 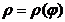 .
.
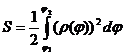
Уравнение Лемниската-Берлуни
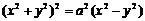
9. Вычисление длины дуги кривой. Пусть заданна 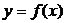 на
на 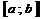 .
. 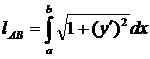
Объемы тел вращения
1. 

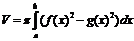
|
|
|
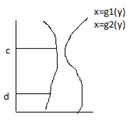
2. 

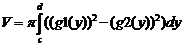

17.Несобственные(н/с) интегралы.
Интегралы с бесконечными пределами
А) н/с интеграл с бесконечным верхним пределом инт.
О1. У=f(x), хЄ[a;+¥) , где а- конечное число. Ф-ция f(x) и интегрируема на любом отрезке [а;B] Ì [a;+¥). (1) 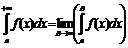 --н/с интеграл с бесконечным верхним пределом
--н/с интеграл с бесконечным верхним пределом
Иногда (1) называют н/с и. первого рода
О2. Если предел в правой части равенства (1) сущ. и явл. конечным числом, то н/с интеграл назыв. сходящимся, в противном случае – расходящимся
Б) н/с интеграл с бесконечным нижним пределом
О3. у= f(x) (-∞;b), которая определена и интегрируемана [А;В]с(-∞;b)
(2) 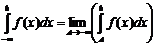 --н/с интеграл с бесконечным нижним пр.
--н/с интеграл с бесконечным нижним пр.
О4. понятие сходимости аналогично
В) н/с интеграл с двумя бесконечн. пределами интегр.
О5. у=f(x) (-∞;+∞), (А;В)с(-∞;+∞)
(3) 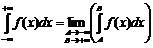 --н/с интеграл с 2мя бесконечн пределами можно переписать как
--н/с интеграл с 2мя бесконечн пределами можно переписать как
(4) 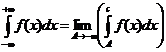
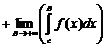 где -∞<С<+∞ , (3)=(4)
где -∞<С<+∞ , (3)=(4)
И. на конечном промежутке
А)пусть ф-ция f(x) определена на конечном промежутке [a,b) и интегрируема на любом отрезке[a,x]Ì[a,b)
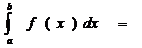
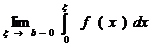
Иногда это выражение называют н/с и. второго рода.
Если конечн предел сущ., то и.  наз. сходящимся, в противном случае – расходящимся.
наз. сходящимся, в противном случае – расходящимся.
Б)н/с интеграл от разрывных функции
пусть задана ф-ция у=f(x) [a;b], причем cÎ[a;b], такая, что ф-ции f(x) в этой точке имеет бесконечный разрыв (x=c – точка разрыва второго рода) , тогда 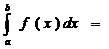

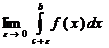 --н/с интеграл от разрывной ф-ции
--н/с интеграл от разрывной ф-ции
|
|
|
Если оба предела в правой части существуют и явл конечными числами, то н/с интеграл разрывн ф-цииназыв сходящимся, а если один из пределов не сущ. или =∞, то н/с интеграл наз. расходящимся
18. Несобственные интегралы от неограниченных ф-й.
Пусть ф-цияопределена и интегрируема на замкнутом промежутке [a;b], за исключением конечного числа точек 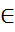 [a;b], в которых ф-ция терпит разрыв 2-го рода. Тогда интеграл наз-ся несобственным интегралом от разрывной ф-ции и вычисляется по правилу:
[a;b], в которых ф-ция терпит разрыв 2-го рода. Тогда интеграл наз-ся несобственным интегралом от разрывной ф-ции и вычисляется по правилу:


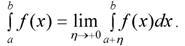
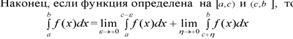
19. Дифференциальное уравнение(ДУ)
Осн.понятия
Дата добавления: 2018-04-05; просмотров: 356; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
