Необходимые условия экстремума

Стр 1 из 8Следующая ⇒

Понятие функции многих переменных Пусть имеется n-перем-х и каждому х1, х2… хn из нек-гомнож-ва х поставлено в соответствие опред. число Z, тогда на множ-ве х задана ф-цияZ=f(х1, х2… хn) многих переменных.

Х – обл-тьопред-я ф-ции

х₁, х₂… х_n – независ-е переем-е (аргументы)

Z – ф-ция Пример: Z=П х²₁*х₂(Объем цилиндра)

Рассм-м Z=f(х;у) – ф-цию 2-х перем-х (х₁, х₂ замен-ся на х,у). Рез-ты по аналогии переносятся на др. ф-ции многих перем-х. Обл-тьопред-я ф-ции 2-х перем-х – вся корд пл-ть (оху) или ее часть. Мн-во знач-й ф-ции 2-х перем-х – поверх-ть в 3х-мерном простр-ве.

Приемы построения графиков: - Рассм-т сечение поверх-типл-тями || координатнымпл-тям.

Пример: х = х₀, зн. пл-ть Х || 0уz у = у₀ 0хz Вид ф-ции: Z=f(х₀,y); Z=f(x,у₀)

Например: Z=x²+y²-2y

Z= x²+(y-1)²-1 x=0 Z=(y-1)²-1 y=1 Z= x²-1 Z=0 x²+(y-1)²-1

Парабола окруж-ть(центр(0;1)

1б.Пределы и непрерывность ф-ций двух переменных

Пусть задана Z=f(х;у), тогда А – предел ф-ции в т.(х₀,y₀), если для любого сколь угодно малого положит. числа E>0 сущ-т полож-е число б>0, что для всех х,уудовл-щих |x-х₀|<б; |y-y₀|<б выполняется нерав-во |f(x,y)-A|<E

Z=f(х;у) непрерывна в т.(х₀,y₀), если: - она опред-на в этой т.; - имеет конеч. предел при х, стрем-ся к х₀ и у к у₀; - этот предел = знач-ю

ф-ции в т.(х₀,y₀), т.е. limf(х;у)=f(х₀,y₀)

Если ф-ция непрерывна в кажд. т. мн-ва Х, то она непрерывна в этой области

Частные производные первого и второго порядка

Производная первого порядка(которая называется частной) Пусть 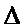х, 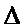у – приращения независимых переменных х и у в некоторой точке из области Х. Тогда величина, равная 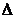z = f(x+ 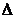х, y+ 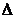у) = f(x,y) называется полным приращением в точке х_0,у_0.Если переменную х зафиксировать, а переменной у дать приращение 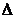у, то получим 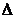zу = f(x,y,+ 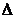у) – f(x,y). Аналогично определяется частная производная от переменной у, т.е.

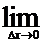
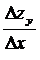
z’_x = Частную производную функции 2-х переменных находят по тем же правилам, что и для функций одной переменной.

Отличие состоит в том, что при дифференциации функции по переменной х , у считается const, а при дифференцировании по у, х считается const.

Для ф-и 2-х переем-х сущ 4 части произв-х 2 порядка:

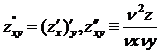
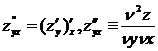
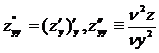
3. Полный дифференциал функции 2-х переменных

Пусть z = f(x,y), тогда dz = 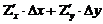- наз полным дифференциалом

Учитывая, что для ф-и f(x,y)=x, f(x,y)=y, df(x,y)=∆x=dx, df(x,y)=∆y=dy, полныйдиф-л можно записать в виде:

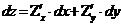
Геометрич смысл. О. Т. 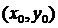назmax(min) ф-и z = f(x,y), если сущнекот окрест-ть . 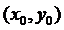такая, что для всех x,y из этой окрест-тивып-сянер-во f(x,y)<f 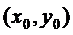(max) или f(x,y)>f (min). Т.: Если задана точка экс-ма ф-и 2-х переем-х , то знач-е частных произв-х в этой точке = 0, т.е. ,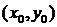

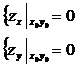
Точки , в которых частные производные первого порядка называются стационарными или критическими.Поэтому для нахождения точек экстремума функции 2-х переменных используются достаточные условия экстремума.

Достатусл-е экстр-ма: Пусть функция z = f(x,y) дважды дифференцируема, и стационарная точка,

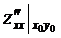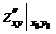A= , B = , C = 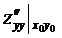, , 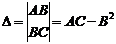тогда

1) 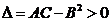, причем max, если A<0, min, если A>0.

2) , экстр-ма в 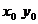т. ет

3) 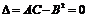, треб-сядописслед-е

приближвыч-яхзнач-й ф-и 2-х переем-х, исп-ся след формула: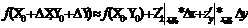

4.Экстремум функции двух переменных

Необходимые условия экстремума

О. Пусть функция z = f(x,y) определена в некоторой 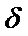- окрестности точки 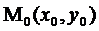. Тогда функция z = f(x,y) имеет в точке 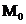максимум(минимум), если для всех точек этой окрестности выполняется неравенство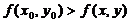

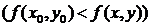
Дата добавления: 2018-04-05; просмотров: 274; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 4 5 6 7 8 Следующая ⇒

Мы поможем в написании ваших работ!