Если подстановка выбрана удачно, то интеграл, получ в правой части, вычисляется проще, чем в исходной

Если ф-цияx=φ(t) непрерывна и монотонна,тообратн. t=ψ(x) всегда сущ.

Вычислив интеграл в правой части по t,следует вернуться к переменной x

∫f(ψ(x)) φ’(x)dx=∫f(t)dt, где t=ψ(x)

1 ∫f(ax+b)dx= ax+b=t, x=(t-b)/a

                    dx=1/a dt

=∫f(t)1/a dt=1/a ∫f(t)dt=1/a F(t)+C=

=1/a F(ax+b)+C

2 ∫ f’(x)/f(x) dx= ln f(x) +C

3 ∫ df(x)/f(x) = ln f(x) +C                                        

Метод интегрирования по частям

Задано: U=U(x), V=V(x),известно: d(UV)=VdU+UdV

проинтегрируем обе части уравнения:

∫ d(UV)= ∫ VdU+ ∫ UdV

UV=∫ VdU+ ∫ UdV=>∫UdV=UV-∫VdU- ф-ла интегр-я по частям

Смысл ф-лыинтегр-я по частям сост в след.: подинтегрвыраж-е UdVразб-ся на 2 части т. о.,чтобы интеграл в правой части вычислялся проще,чем исходный.

Основные классы ф-ций,интегрируемых по частям:

1 ∫ ln^m(x)dx, ∫arcsin^mxdx, ∫arccos^mxdx,∫arctg^mxdx

2 ∫Pn(x)lnaxdx,∫Pn(x)e^axdx,∫ Pn(x)sinaxdx,

∫Pn(x)cosaxdx

3 ∫e^axsinbxdx,∫e^axbxdx

4 ∫ (x²+a²)½dx, ∫(a²- x²)½dx, ∫ dx/(x²+a²)^k

Интегрирование выражений, сод-х квадратный трехчлен

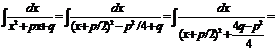x+p/2=t dx=dt a²=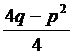 или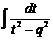

IV

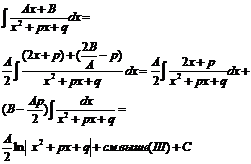
V. 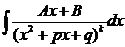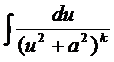p²/4-q>0

p²/4-q<0

10. Интегрирование рациональных дробей

1. Многочленом степени nназ-ся выражение вида a₀+a₁x+a₂x²+…+a_nxⁿ=P_n(x)

Рациональной дробью наз-ют отношение двух многочленов вида 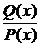При n=0 вычисление интеграла никаких трудностей не представляет

Интерес представляют рациональные дроби, у кот. n>0 При этом будем рассматривать дроби, у кот. m<n Если m>=n, то применяют процедуру деления многочленов уголком

Интегрирование простейших дробей

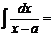I. x-a=tdx=dt

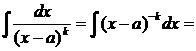II. x-a=tdx=dt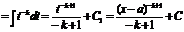

11 Определение опред. интеграла

Пусть зад ф у=f(x), кот непрер на некот. замкнутоминт-ле [a,b].

Разбиваем инт-л [a,b] на n частей; абсциссы точек дел-яa=x₀<x₁<x₂<…<x_i-1<x_n-1<x_n=bобознx₁,x₂,…x_n. Кажд частичный инт-л обозн ∆x₁=x₁-x₀, ∆x₂=x₂-x₁, ∆x_i=x_i-x_i-1, ∆x_n=x_n-x_n-1. В каждом частичном инт-ле ∆x_i, i= 1;n выберем т. и выч-мﻉ_I, y=f(x), y=f(ﻉ₁) , f(ﻉ₂) , … f(ﻉ_i) ,… f(ﻉ_n) Cост-м произв-е f(ﻉ₁)∆x₁, f(ﻉ₂)∆x₂ , … f(ﻉ_i)∆x_i ,… f(ﻉ_n)∆x_n.Кажд из этих произв-й предст собой полоску шириной ∆x_iи высотой f(ﻉ_i).

О1. Сумма f(ﻉ₁)∆x₁+ f(ﻉ₂)∆x₂ + … f(ﻉ_i)∆x_i +… f(ﻉ_n)∆x_n=∑ f(ﻉ₁)∆x₁ назинтегр суммой ф. f(x) на инт-ле [a,b]. С геом. точки предст собой S ступенчатой фигуры.

Обозн наиб.из разностей ∆x₁₌x_i-x_i-1 через ОХ. Тогда имеет место определение 2.

О2. Сущ кон предел интегр ∑, т.е. 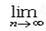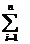f(ﻉ₁)∆x₁ и он не зав-т от СП-ба разбиения инт-ла [a,b] и выбора точекﻉ₁ на частичных инт-лах ∆x_i, то этот предел назопред интегралом ф. f(x) на [a,b] и обозн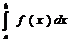

Т. Для всякой непрерф-и интеграл сущ.

А Геом. смысл опред. интеграла.

Опред интеграл опред-т точноезн-е Sкриволинтр-и.

 

12. Оснсв-ваопред интеграла 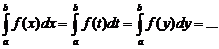 Значение о.и. не зависит от обозначения переменной интегрирования.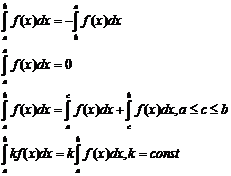

Если 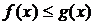, x € [a;b]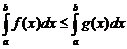

Формула Ньютона-Лейбница (вывод)

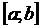Т:          Если  непрерывна на  , справедлива ф-ла Ньютона-Лейбница: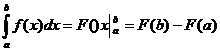

Рассм-м 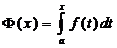 , т.к. 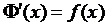, то 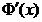- первообразная для 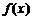. Но 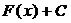, также первообразная. Это значит что имеет место следующее равенство :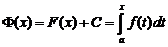

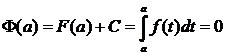Подставим верхнюю границу: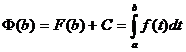 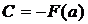  подставами вместо  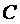 : в силу 1-го свойства, что значении определенного интеграла независит от обозначения переменной интегрирования,запишем: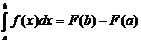                                         

---

Дата добавления: 2018-04-05; просмотров: 352; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!