Решение экзаменационной контрольной работы
1. Вектор скорости частицы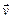 
связан с радиус-вектором 
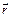соотношением
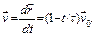
Для интегрирования этого дифференциального уравнения имеем начальное условие
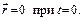
Интегрирование дает
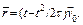
Это уравнение описывает прямолинейное движение с постоянным ускорением. Такое обстоятельство позволяет ввести координату по направлению вектора начальной скорости (пусть это будет ось x) и вместо векторного уравнения рассматривать алгебраическое:
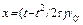
По условию задается расстояние S от начала координат. Другими словами, координата x принимает два значения: x = ± S. Решаем квадратное уравнение:
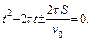
Находим корни этого уравнения:
При x = S решением задачи является корень
При этом, однако, на величину расстояния S накладывается ограничение:
(Решение должно быть действительным числом.) В заданной точке частица побывает дважды: первый раз – при выборе знака минус, второй раз – при знаке плюс. Такую ситуацию поясняет рисунок, приведенный ниже.
|
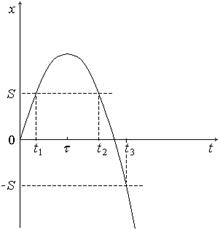
При x = – S решением задачи является один корень:
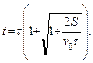
Знаку минус перед квадратным корнем отвечает отрицательное значение времени.
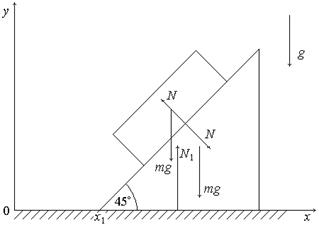
2. На клин действуют сила тяжести, реакция опоры со стороны гладкой горизонтальной плоскости и сила давления со стороны бруска. Проекцию на горизонтальное направление (ось x) дает только последняя сила. Она и вызывает ускоренное движение клина.
|
Напишем уравнение движения для клина:
При поступательном движении твердого тела все его точки имеют одновременно одну и ту же скорость и, следовательно, одинаковое ускорение. Поэтому в качестве ускорения клина можно взять ускорение его левой точки с координатой x 1.
|
|
|
Напишем уравнения движения для бруска:
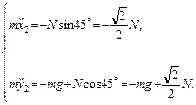
Здесь x 2, y 2 – координаты левой нижней точки бруска. Так как брусок скользит по клину, то координаты выбранной точки бруска связаны с координатами выбранной точки клина геометрическим соотношением
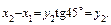
Дважды дифференцируя это соотношение по времени, складывая уравнение для клина с первым из уравнений для бруска и складывая уравнения системы для бруска, получим систему уравнений:
Сложение всех уравнений полученной системы дает проекцию ускорения бруска на ось x:
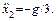
Тогда из второго уравнения системы найдем ускорение клина:
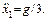
3. На брусок, лежащий на доске, действуют сила тяжести, нормальная реакция опоры со стороны доски и сила трения. Введем ось x вдоль доски и напишем 2-й закон Ньютона в проекции на эту ось:
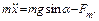
При относительно малых углах α между доской и полом брусок остается неподвижным и сила трения, действующая на брусок, в соответствии со 2-м законом Ньютона равна
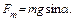
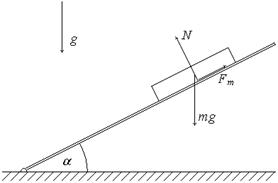
При увеличении угла α, начиная с некоторого его значения, брусок скользит по доске с постоянным ускорением. При этом сила трения определяется нормальной реакцией опоры со стороны доски:
|
|
|
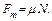
Проектируя все силы на нормаль к доске, найдем нормальную составляющую силы реакции опоры:
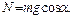
В результате сила трения при скольжении бруска равна
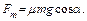
При этом ускорение бруска равно
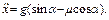
В соответствии с выбором направления оси x брусок должен скользить по доске с положительным ускорением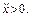 
Условием этого является выполнение неравенства
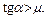
Таким образом, сила трения зависит от угла α следующим образом:
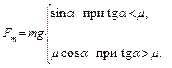
Ниже на рисунке приведен график зависимости силы трения, действующей на брусок, от угла между доской и полом.
|
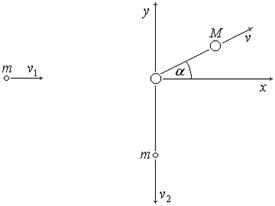
4. Введем декартову систему координат: ось x направим по первоначальному направлению движения частицы массы m, а ось y – по направлению, противоположному направлению ее движения после столкновения со второй частицей. Запишем закон сохранения импульсов в проекциях на оси x и y:
|
Так как соударение частиц происходит абсолютно упруго, то кинетическая энергия системы сохраняется. В этом случае закон сохранения энергии имеет вид
Исключая из уравнений приведенной выше системы угол α, получаем квадрат скорости частицы массы M:
|
|
|
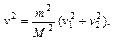
Подставляя полученное выражение для v 2 в уравнение энергии, найдем искомую массу M:
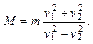
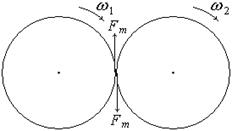
5. При соприкосновении шероховатых цилиндров боковыми поверхностями возникают силы трения. Под действием их моментов угловые скорости цилиндров изменяются до тех пор, пока не выровняются по величине, причем цилиндры будут вращаться в противоположных направлениях. После этого будет происходить чистое качение одного цилиндра по другому (в точке соприкосновения линейные скорости равны; трение отсутствует).
Записываем уравнения моментов для каждого из цилиндров до наступления режима чистого качения, получаем систему уравнений:
Здесь учтено, что оба цилиндра одинаковые: их моменты инерции равны J, радиусы равны R.
|
Из этой системы получаем, что угловые ускорения цилиндров равны между собой:
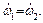
Пусть после наступления режима чистого качения левый цилиндр продолжает вращаться в прежнем направлении с угловой скоростью ω, а правый – в противоположном направлении. (Это допущение несущественно, и конечный результат не зависит от него.) Тогда из равенства ускорений получим, интегрируя его, равенство приращений угловых скоростей:
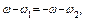
откуда находим величину угловых скоростей вращательного движения цилиндров после их длительного соприкосновения:
|
|
|
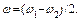
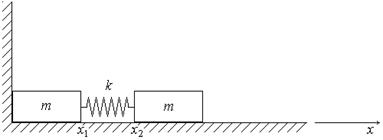
6. На первом этапе пружина разжимается, правый брусок приходит в движение и ускоряется, а левый брусок остается неподвижным до тех пор, пока длина пружины меньше ее длины в недеформированном состоянии (сжатая пружина прижимает левый брусок к стенке). Максимальная скорость правого бруска может быть получена из закона сохранения энергии. Согласно этому закону потенциальная энергия сжатой пружины переходит в кинетическую энергию бруска:
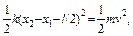
откуда следует
|
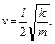
После этого момента правый брусок по инерции продолжает двигаться, длина пружины увеличивается и упругая сила, возникающая при растяжении пружины, отрывает левый брусок от стенки. С этого момента начинается свободное движение системы. Это движение описывается системой дифференциальных уравнений. Согласно 2-му закону Ньютона имеем:
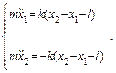
Начальные условия принимают вид
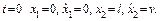
Складывая уравнения системы и вычитая из второго первое, приводим систему к виду
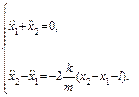
Однократное интегрирование первого уравнения этой системы с учетом начальных условий дает
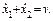
Его можно получить из закона сохранения импульса. Для решения задачи оно не представляет интереса.
Во втором уравнении величина (x 2 – x 1 – l) представляет растяжение пружины. Обозначая ее через Δ x, перепишем данное уравнение:
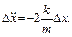
Это уравнение гармонических колебаний. Оно должно решаться при начальных условиях:
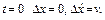
Его решение имеет вид
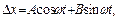
где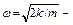 
частота колебаний. Постоянные коэффициенты A и B находятся из начальных условий. Первое условие дает A = 0. Из второго условия находим B = v / ω. Подставляя полученное выше выражение для скорости правого бруска после первого этапа движения системы, найдем 
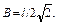В результате решение уравнения гармонических колебаний системы имеет вид
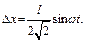
Длина пружины зависит от времени следующим образом:
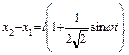
Максимальное и минимальное значения длины пружины равны соответственно
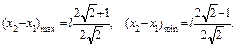
Переэкзаменовка
1. (120 б.) Покинув источник, частица пролетает с постоянной скоростью расстояние l, а затем тормозится с постоянным ускорением a. При какой скорости вылета частицы из источника время ее движения до остановки будет минимальным?
2. (150 б.) К концам перекинутой через невесомый блок нерастяжимой невесомой нити привязаны грузы массой m 1 и m 2. Блок подвешен к пружинным весам. Каковы показания весов при свободном движении грузов?
|
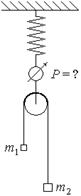
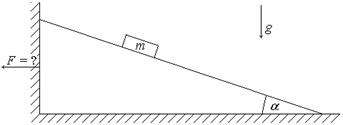
3. (180 б.) Клин с углом наклона α лежит на гладкой горизонтальной плоскости, упираясь в стенку. На него кладут груз массой m. С какой силой клин давит на стенку? Коэффициент трения груза о клин равен μ.
|
4. (180 б.) Два бруска с массами m 1 и m 2 одновременно начинают соскальзывать навстречу друг другу с горок высотой h. При столкновении бруски слипаются. На какую высоту поднимутся бруски после столкновения? Бруски движутся без трения.
|
5. (220 б.) Однородный диск массой m подвешен на двух одинаковых нитях в точках A и B, расположенных на одной горизонтали. Угол AOB равен 2 α. Правую нить перерезают. Найти силу натяжения левой нити сразу после того, как будет перерезана правая нить.
|
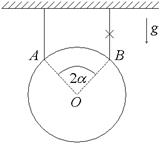
6. (250 б.) Две одинаковые тонкие невесомые струны длиной l расположены в одной плоскости и натянуты с силой T. На серединах струн закреплены грузы массой m каждый. Грузы связаны недеформированной пружиной жесткости k. Найти частоты малых нормальных колебаний системы и нормальные координаты. Колебания происходят в плоскости, проходящей через струны.
|
Примечание. В задачах 2–5 предполагается наличие однородного поля тяжести с ускорением свободного падения g.
Дата добавления: 2015-12-20; просмотров: 56; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!