Блочно-диагональная форма
Рассмотрим SISO-систему, заданную передаточной функцией (16). Рассмотрим приведение передаточных функций к уравнениям состояния, представленным диагональной (жордановой) формой матрицы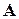 
. Пусть корни характеристического многочлена являются простыми. В этом случае всегда имеется возможность разложить W(s) на простейшие слагаемые первого и второго порядков, т.е. записать ее в виде (5), как 
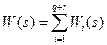, где
Для каждого слагаемого (в произвольно выбранном порядке) заполняются клетки матрицы 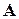, имеющей вещественную форму Жордана (4)
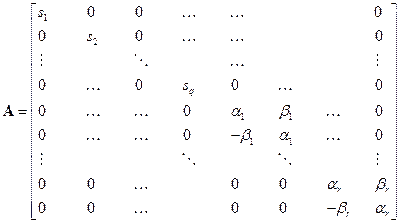
Элементы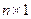 
-матрицы 
и 
-матрицы 
находятся таким образом, чтобы соответствующая данному входу передаточная функция из (5) имела заданные коэффициенты числителя.
Если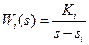 
, то элементы должны удовлетворять условию 
.
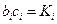Для блоков второго порядка с передаточной функцией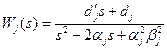 
коэффициенты числителя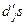 
, 
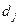связаны с элементами матриц 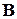и 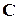соотношениями
.
Эти условия дают возможность выбрать искомые элементы, причем задача также решается неоднозначно
Жорданова форма
Если передаточная функция системы имеет кратные полюса, ее разложение будет содержать слагаемые, степени знаменателей которых отвечают значениям кратности. Для вещественных корней кратности k получаются знаменатели k-й степени, для мнимых корней - степени 2к. Тогда W(s) имеет вид (5), (9). Исходя из найденных при разложении передаточной функции W(s) слагаемых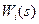 
указанного вида нетрудно записать матрицу 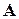в форме Жордана (6), в которой вещественным корням соответствуют диагональные блоки вида (7), а мнимым - блоки вида (8). Элементы матриц 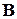, 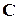можно получить путем обратных вычислений методом неопределенных коэффициентов.
|
|
|
Например, для вещественных корней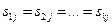 
(кратности 
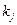) можно представить 
в виде
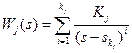
Если выбрать элементы соответствующих строк матрицы 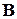в виде 
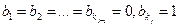, то соответствующие данной клетке элементы матрицы С определяются равенствами 
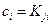. Другой возможный выбор – положить 
, а остальные элементы подстроки - равными нулю. Тогда значения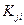 
, взятые в обратном порядке, присваиваются элементам 
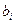. Явный вид уравнений состояния для вещественных корней характеристического многочлена A(s) приведен в [94].
Замечание 1. Процесс преобразования передаточной функции к блочно-диагональной и жордановой формам существенно более трудоемок, чем преобразования к виду УКП или НКП, так как связан с разложением передаточной функции на слагаемые и вычислением корней характеристического многочлена.
Замечание 2. Приведенные выше уравнения рассмотрены для непрерывных систем, однако канонические формы и методы получения уравнений состояния по передаточным функциям с очевидным изменением обозначений применимы и к дискретным системам.
|
|
|
Применение MATLAB к преобразованию систем к каноническим формам.
Для начала вернёмся к процедуре вычисления собственных значений и собственных векторов матрицы .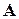
1. Основная функция MATLAB, решающая проблему собственных значений –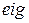 
.
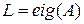– столбец 
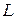заполняется собственными числами матрицы .
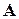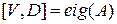– диагональная матрица 
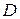содержит собственные числа; столбцы матрицы 
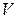- соответствующие им собственные векторы (нормированные). Имеет место соотношение 
.
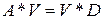>>A=[4 -1 -2;2 1 -2;1 -1 1]
A =
4 -1 -2
2 1 -2
1 -1 1
>> L=eig(A)
L =
1.0000
3.0000
2.0000
>> [V,D]=eig(A)
V =
-0.5774 -0.7071 0.7071
-0.5774 -0.7071 -0.0000
-0.5774 -0.0000 0.7071
D =
1.0000 0 0
0 3.0000 0
0 0 2.0000
Если среди корней вещественной матрицы имеются комплексные, по команде 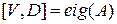будут созданы комплексные матрицы 
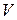и .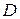
> A=[4 -1 -2;2 1 -1;1 -1 1];
>> L=eig(A)
L =
3.0000
1.5000 + 0.8660i
1.5000 - 0.8660i
>> [V,D]=eig(A)
V =
-0.7071 0.2887 + 0.5000i 0.2887 - 0.5000i
-0.7071 0.5774 0.5774
-0.0000 0.2887 + 0.5000i 0.2887 - 0.5000i
D =
3.0000 0 0
0 1.5000 + 0.8660i 0
0 0 1.5000 - 0.8660i
Для получения вещественных матриц 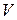и 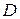надо применить команду 
, где матрица 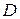будет блочно-диагональной – каждой паре комплексно-сопряжённых корней соответствует диагональный 2х2 блок.
>> [V,D]=cdf2rdf(V,D)
V =
-0.7071 0.2887 0.5000
-0.7071 0.5774 0
-0.0000 0.2887 0.5000
D =
3.0000 0 0
0 1.5000 0.8660
0 -0.8660 1.5000
|
|
|
2. Разложение Жордана.
В MATLAB жорданово разложение находится с помощью команды [ 
V,J]= jord(A).
При наличии кратных корней характеристического полинома квадратную матрицу А не всегда можно привести к диагональному виду, т.е. представить как произведени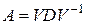е 
, где 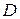диагональная матрица. Однако всегда можно построить более общее разложение 
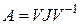, где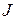 
- жорданова форма матрицы 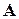, которая представляет собой блочно-диагональную матрицу с жордановыми клетками
,
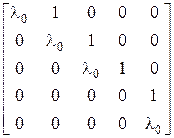где 
- корень характеристического уравнения. Каждому корню соответствует одна или несколько клеток-блоков, их порядки могут быть любыми. Число блоков, соответствующих , равно геометрической кратности этого корня, сумма порядков блоков, соответствующих , равна алгебраической кратности корня.
Алгебраическая кратность собственного значения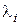 
– это кратность данного корня в характеристическом полиноме.
Геометрическая кратность собственного значения 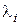- кратность данного корня в минимальном полиноме 
.
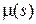Минимальный полином – минимальный аннулирующий полином матрицы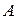 
.
Чаще соотношение между матрицам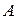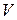и , и 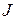записывают иначе: 
.
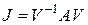Применим разложение Жордана для простых корней
>> A=[4 -1 -2;2 1 -1;1 -1 1];
>> [V,J]=jordan(A)
V =
1.0000 0 - 0.5774i 0 + 0.5774i
|
|
|
1.0000 -0.5000 - 0.2887i -0.5000 + 0.2887i
0 0 - 0.5774i 0 + 0.5774i
J =
3.0000 0 0
0 1.5000 + 0.8660i 0
0 0 1.5000 - 0.8660i
Для получения вещественных матриц 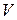и 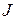надо применить команду 
,
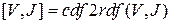>> [V,J]=cdf2rdf(V,J)
V =
1.0000 0 -0.5774
1.0000 -0.5000 -0.2887
0 0 -0.5774
J =
3.0000 0 0
0 1.5000 0.8660
0 -0.8660 1.5000
Рассмотрим применение разложения Жордана для кратных корней.
>> A=[11 4;-4 3];
>> [V,J]=jordan(A)
V =
4 1
-4 0
J =
7 1
0 7
Заданный характеристической полином имеет вещественный корень 7, алгебраическая кратность корня равна 2, геометрическая кратность равна 1, поэтому разложение содержит одну клетку размером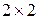 
.
Пусть характеристический полином матрицы 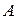имеет комплексные корни 
.
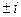алгебраическая кратность корня равна 2, геометрическая кратность корня равна 1, этому корню соответствует жорданова клетка .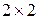
>> A=[0 -2 0 -1;1 0 0 0;0 1 0 0;0 0 1 0];
>> [V,J]=jordan(A)
V =
0 + 0.2500i 0.5000 0 - 0.2500i 0.5000
0.2500 0 - 0.2500i 0.2500 0 + 0.2500i
0 - 0.2500i 0 0 + 0.2500i 0
-0.2500 0 - 0.2500i -0.2500 0 + 0.2500i
J =
0 + 1.0000i 1.0000 0 0
0 0 + 1.0000i 0 0
0 0 0 - 1.0000i 1.0000
0 0 0 0 - 1.0000i
Для вещественных кратных корней может быть использована функция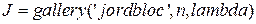 
, которая возвращает блок Жордана порядка n с собственным значением 
.
J=gallery('jordbloc',5,-2)
J =
-2 1 0 0 0
0 -2 1 0 0
0 0 -2 1 0
0 0 0 -2 1
0 0 0 0 -2
Для работы с формами Жордана можно обратиться к модулю 
ППП 
либо к пакету программ 
.
3. Получение канонических форм уравнений состояний по передаточной функции.
Литература
1. Андреев Ю.Н. Управление конечномерными линейными объектами. М.: Наука, 1976.
2. Ланкастер П. Теория матриц. М.: Наука, 1978.
3. Математические основы теории автоматического регулирования: Учебное пособие/ Под ред. Б.К. Чемоданова
4. Первозванский А.А. Курс теории автоматического управления: Учеб пособие. - М.: Наука, 2010.
5. Андриевский Б.Р., Фрадков А.Л. Избранные главы теории автоматического управления с примерами на языке MATLAB. – СПб.: Наука, 1999.
6. Б.Т. Поляк, П.С. Щербаков. Робастная устойчивость и управление. М.: Наука, 2002.
7. Кетков Ю.Л., Кетков А.Ю., Щульц М.М. MATLAB 7: Программирование, численные методы. – СПб.: БВХ – Петербург, 2005.
Дата добавления: 2015-12-18; просмотров: 60; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!