Канонические формы уравнений состояния
Имеется множество эквивалентных (с точки зрения входо-выходных соотношений) способов представления уравнений состояния системы, однако можно выбрать из них “наилучшие” – наиболее удобные для использования в рассматриваемой задаче. Такие формы записи уравнений называются каноническими [1,2,3]. Рассмотрим некоторые, наиболее распространенные из них. Основное внимание будет уделяться системам с одним входом и выходом (SISO).
Диагональная и жорданова формы
Пусть собственные числа матрицы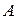 
заданы и равны 
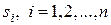. Рассмотрим следующие случаи:
Простые вещественные собственные числа.
Пусть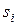 
- простые, вещественные, т.е. 
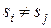при 
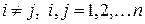и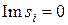 
. В этом случае любую матрицу 
можно привести с помощью некоторого невырожденного преобразования к диагональной матрице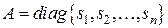 
или матрице вида
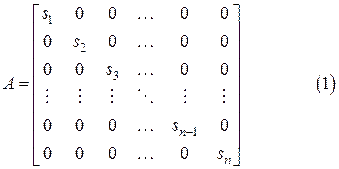
Множество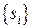 
образует спектр матрицы . Найдем характеристическую матрицу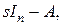 
которая тоже является диагональной, 
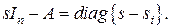Характеристический многочлен есть определитель данной матрицы, а для диагональной матрицы он равен произведению элементов главной диагонали 
.
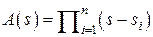Полученный базис удобен тем, что в нем уравнения системы распадаются на уравнения 
независимых подсистем первого порядка. Приведем уравнения состояния “в развернутом виде”, т. е. в виде системы уравнений первого порядка относительно компонентов вектора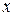 
, есл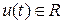и 
и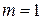 
. Получим
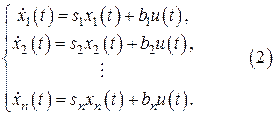
Переменная состояния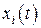 
не зависят от 
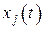(при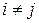 
). Следовательно, происходит декомпозиция системы – система высокого ( -го) порядка распадается на независимых подсистем меньшего (первого) порядка. Вследствие этого упрощается расчет процессов в системе.
|
|
|
Посмотрим, какая структура системы соответствует такой форме матрицы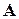 
с точки зрения передаточных функций. Пусть 
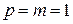- система имеет один вход и один выход, 
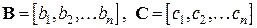. Из (2) получаем, что передаточные функции к 
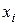определяются выражениями 
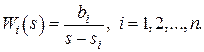Учитывая уравнение выхода 
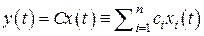, получим, что передаточная функция всей системы имеет вид
.
Таким образом, диагональная форма матрицы соответствует системе, состоящей из параллельно соединенных подсистем первого порядка (апериодических или интегрирующих звеньев).
Простые мнимые собственные числа
Более сложным случаем является наличие у матрицы невещественных (комплексно-сопряженных) корней. Как и выше, при простых собственных числах, матрица 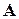также может быть приведена невырожденным преобразованием к диагональному виду (1), однако такая матрица будет содержать на диагонали мнимые элементы. Это неудобно для дальнейшего ее использования. Для устранения указанной трудности используется квазидиагональная (блочно-диагональная) форма. При таком представлении мнимым корням 
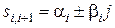характеристического многочлена соответствуют блоки (клетки) вида
|
|
|
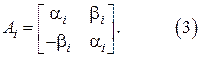
Характеристический многочлен матрицы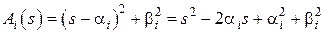 
. Корни этого многочлена 
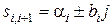совпадают с заданными. Окончательно матрица имеет следующую блочную структуру (определенную с точностью до порядка следования блоков):
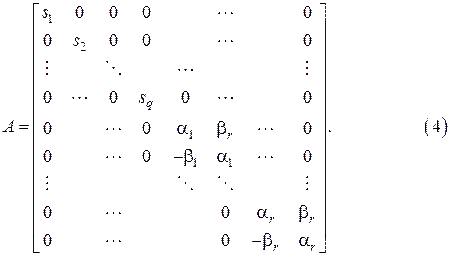
Вещественным корням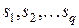 
характеристического многочлена соответствуют блоки размера 
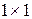, мнимым корням 
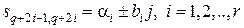соответствуют блоки размера 
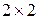вида (3).
Вычисляя характеристический многочлен матрицы (4), получим
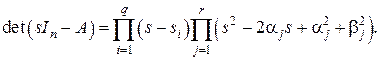
Таким образом, матрица 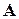имеет заданные собственные числа 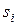. Если снова записать уравнения состояния для каждой компоненты вектора 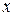, то система “распадается” на 
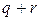независимых подсистем первого и второго порядков.
При 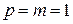передаточная функция системы принимает вид
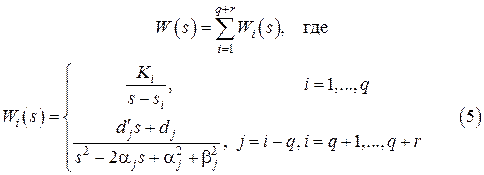
Такой форме уравнений состояния соответствует разложение передаточной функции системы на слагаемые первого и второго порядков, что иллюстрируется на рисунке 1.
Рассмотренные выше канонические формы матрицы 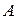(1) и (4) представляют собой частные случаи так называемой вещественной формы Жордана. Такая форма может быть получена, если характеристический многочлен матрицы 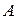не имеет кратных корней.
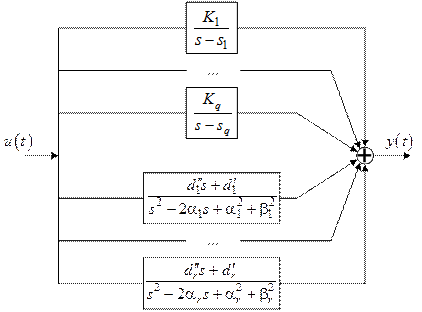
Рис. 1. Структурная схема, соответствующая жордановой форме (4).
Дата добавления: 2015-12-18; просмотров: 35; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!