Общий случай. Вещественная форма Жордана
При наличии кратных корней матрица не может быть невырожденным преобразованием приведена к диагональной или блочно-диагональной форме (1), (4).
Общий блочно-диагональный канонический вид матрицы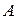 
для кратных собственных чисел при любой исходной матрице называется вещественной (обобщенной) жордановой матрицей (6).
Жордановой матрицей называется клеточно-диагональная матрица, в которой на главной диагонали стоят клетки Жордана, а все элементы вне этих клеток равны нулю. В этой форме матрица 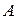имеет следующую блочную структуру (также говорят, что матрица 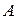представлена в собственном базисе):
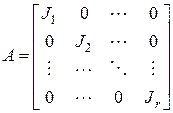, (6)
где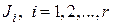 
- клетки Жордана.
Квадратная матрица размера 
, элементы главной диагонали которой равны числу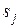 
, а элементы 
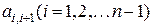- единицы, а все остальные элементы – нули, называется клеткой Жордана порядка n, соответствующей собственному значению .
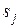Для вещественных собственных чисел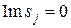 
клетка Жордана имеет вид:
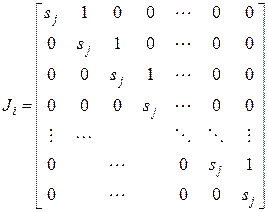(7)
Для собственных чисел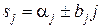 
клетка Жордана имеет вид:
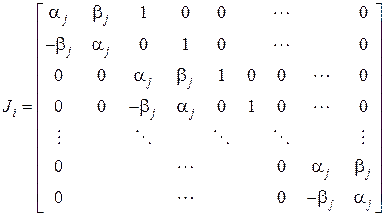(8)
Из теории матриц [1,2] известна следующая теорема.
ТЕОРЕМА. Всякая квадратная матрица над полем вещественных чисел подобна некоторой обобщенной жордановой матрице, которая определяется однозначно с точностью до порядка расположения клеток на главной диагонали.
Размер каждой клетки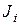 
вида (7) может быть от 
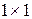до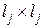 
, а размеры клеток 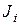вида (8) – от 
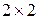до 
, где 
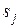- кратность корня . Следовательно, в случае простых корней клетки, отвечающие вещественным собственным числам, имеют порядок один: 
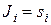, а клетки, отвечающие мнимым собственным числам – порядок два: 
Таким образом, приведенная выше форма (4) следует из (6) как частный случай.
|
|
|
Существенно, что размер клеток Жордана в общем случае не совпадает с кратностью корня. Одному и тому же значению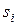 
может отвечать несколько клеток разного размера. Например, существуют матрицы 
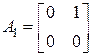и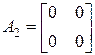 
, которые имеют одинаковые наборы собственных чисел 
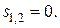Обе матрицы записаны в канонической жордановой форме, но матрица 
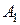совпадает с клеткой 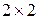, а матрица 
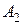содержит две клетки 
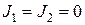размера 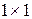. Данные матрицы не могут быть преобразованы одна к другой никаким невырожденным преобразованием, т. е. они не являются подобными. В этом проявляется общее свойство матриц, согласно которому каноническая форма Жордана определяется единственным образом с точностью до порядка следования клеток [53, 115].
Вычисление передаточной функции системы с одним входом и одним выходом, представленной уравнениями с матрицей (6), дает следующий результат. Передаточная функция 
, как и для случая простых собственных чисел, имеет вид (5), где соответствующие слагаемые равны
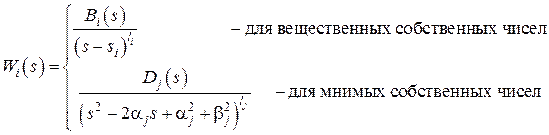(9)
в которых многочлены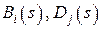 
имеют степени 
и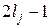 
соответственно.
|
|
|
Алгоритм определения размеров клеток Жордана для матриц с кратными собственными числами связан с выполнением следующих действий:
– составление характеристической матрицы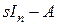 
и приведение ее к каноническому виду;
– вычисление элементарных делителей матрицы ;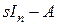
– построение клеток Жордана по каждому элементарному делителю.
Этот процесс достаточно трудоемок и здесь не рассматривается.
Управляемое каноническое представление
Рассмотрим одну из канонических форм – управляемое каноническое представление (УКП) [1,2,3,5,6], которая иногда называется также канонической формой “ c общим выходом ”, канонической формой фазовой переменной либо управляемой матрицей Луенбергера.
Запишем матрицу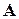 
в виде
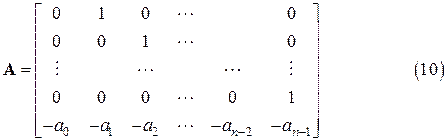
где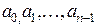 
- некоторые коэффициенты. Вычислим ее характеристический многочлен 
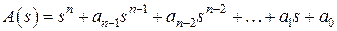. Коэффициенты характеристического многочлена располагаются в последней строке матрицы 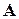. Матрицы такого вида называются сопровождающими для своего характеристического многочлена, или матрицами Фробениуса (иногда используется запись 
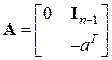). Данные матрицы обладают рядом интересных свойств, в частности, коэффициенты характеристического многочлена таких матриц определяются без вычислений.
|
|
|
Матрица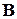 
для данной канонической формы также имеет специальный вид. Остановимся на частном случае систем со скалярным входным воздействием 
, т. е.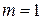 
.
Для таких систем матрица 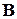имеет размер 
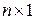и может рассматриваться как вектор-столбец. В данной канонической форме выполнено равенство
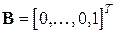(11)
Следовательно, уравнения состояния системы в данной канонической форме имеют вид
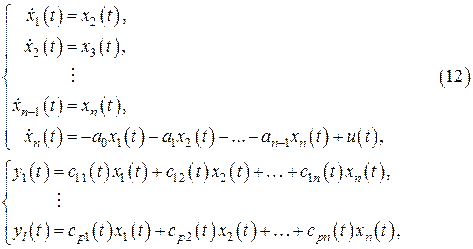
где через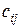 
обозначены элементы 
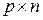матрицы 
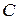, вид которой не оговаривается. Переменные состояния системы (12) связаны друг с другом как последовательные производные. Такая форма уравнений обычно используется при приведении дифференциального уравнения 
-го порядка к системе уравнений первого порядка, т.е. к так называемой нормальной форме Коши [2]. Структурная схема системы с одним выходом, уравнения которой имеют вид (12), показана на рис. 2.
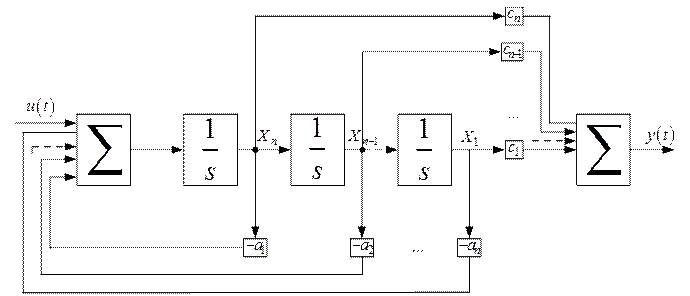
Рис. 2. Структурная схема системы (12) (форма УКП).
Получим передаточную функцию системы (12), если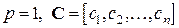 
. Непосредственное вычисление приводит к выражению
В данной канонической форме коэффициенты знаменателя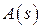 
и коэффициенты числителя 
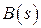передаточной функции находятся без вычислений. Они получаются непосредственно из элементов последней строки матрицы 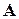и соответствующей 
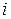-му выходу строки матрицы 
.
|
|
|
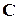Дата добавления: 2015-12-18; просмотров: 30; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!