Свойства степенной функции с рациональным показателем, связанные с неравенствами
Предложение 1. Если 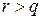 , то
, то 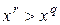 на
на 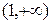 и
и  на
на 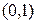 для любых рациональных r и q.
для любых рациональных r и q.
Доказательство. Если 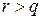 , то
, то 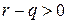 . По свойству степенной функции с положительным рациональным показателем (предложение 10, (1)) на интервале
. По свойству степенной функции с положительным рациональным показателем (предложение 10, (1)) на интервале 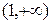 выполняется неравенство
выполняется неравенство 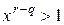 . Умножая обе его части на хq, получаем
. Умножая обе его части на хq, получаем 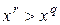 . Для интервала
. Для интервала 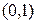 рассуждения аналогичны.
рассуждения аналогичны.
Предложение 2. Функция 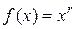 ,
, 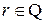 , на
, на 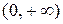 принимает только положительные значения.
принимает только положительные значения.
Доказательство следует из свойств функции 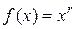 при r > 0 и
при r > 0 и
r < 0, рассмотренных в п. 5 § 12 и п. 5 §13.
§ 15. Определение степени действительного числа
с иррациональным показателем
Прежде чем дать определение степени действительного числа с произвольным действительным показателем и обосновать его корректность, проведем некоторые вспомогательные рассуждения.
Неравенство Бернулли: 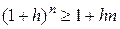 для любых действительного
для любых действительного 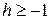 и натурального п.
и натурального п.
Доказательство. Применим метод математической индукции. При п = 1 неравенство очевидно выполняется. Предположим, что оно выполняется при п и осуществим индуктивный переход:
 .
.
На основании ММИ заключаем, что неравенство справедливо при любом натуральном п.
Лемма. 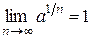 при любом действительном
при любом действительном 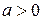 .
.
Доказательство. Требуется доказать:
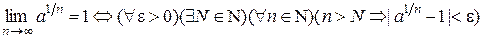 .
.
Рассмотрим случай 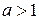 .
.
Обозначим 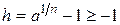 . По неравенству Бернулли получаем:
. По неравенству Бернулли получаем:  для любого
для любого 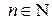 . Отсюда
. Отсюда
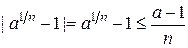 (*).
(*).
Для произвольного 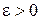 рассмотрим неравенство
рассмотрим неравенство 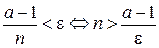 .
.
Возьмем натуральное число N, удовлетворяющее неравенству 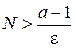 (такое N существует, так как множество натуральных чисел неограниченно сверху). Тогда для всех натуральных
(такое N существует, так как множество натуральных чисел неограниченно сверху). Тогда для всех натуральных 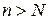 будет выполнено
будет выполнено 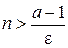 , отсюда
, отсюда 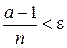 , и в силу неравенства (*) имеем:
, и в силу неравенства (*) имеем: 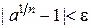 . Следовательно,
. Следовательно, 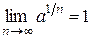 .
.
|
|
|
Рассмотрим случай 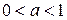 . Тогда
. Тогда 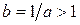 . По доказанному выше
. По доказанному выше 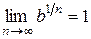 . Используя свойства степеней, имеем:
. Используя свойства степеней, имеем:

Предложение. 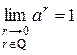 при любом действительном
при любом действительном 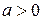 .
.
Доказательство. При а = 1 утверждение очевидно.
Рассмотрим случай 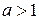 . Требуется доказать:
. Требуется доказать:
 .
.
Возьмем произвольное 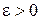 . Поскольку
. Поскольку 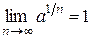 по лемме 13 и
по лемме 13 и 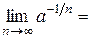
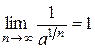 ,то все члены последовательностей
,то все члены последовательностей 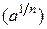 и
и  с номерами, большими некоторого
с номерами, большими некоторого  , принадлежат интервалу
, принадлежат интервалу 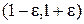 . Пусть
. Пусть 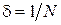 . Возьмем произвольное рациональное r, удовлетворяющее неравенству
. Возьмем произвольное рациональное r, удовлетворяющее неравенству 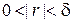 . Очевидно,
. Очевидно,  , поэтому найдется такое натуральное п, для которого будет выполнено:
, поэтому найдется такое натуральное п, для которого будет выполнено: 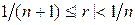 . Тогда по свойству степенной функции с рациональным показателем (предложение 1, § 14) имеем:
. Тогда по свойству степенной функции с рациональным показателем (предложение 1, § 14) имеем: 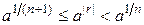 и
и  . Поскольку п -ый и (п+ 1)-ый члены последовательностей
. Поскольку п -ый и (п+ 1)-ый члены последовательностей 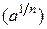 и
и  при
при 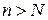 принадлежат интервалу
принадлежат интервалу 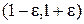 , то
, то 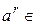
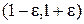 , т. е.
, т. е. 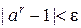 . Следовательно,
. Следовательно, 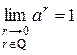 .
.
Рассмотрим случай 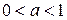 . Тогда
. Тогда 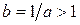 и
и 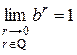 по доказанному выше. Используя свойства степеней, имеем:
по доказанному выше. Используя свойства степеней, имеем:
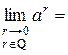
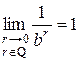 .
.
Определение. Степенью действительного числа 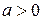 с иррациональным показателем a называется число
с иррациональным показателем a называется число  , где
, где 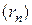 – произвольная последовательность рациональных чисел, сходящаяся к a.
– произвольная последовательность рациональных чисел, сходящаяся к a.
Дата добавления: 2015-12-17; просмотров: 27; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
