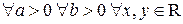Свойства степени с действительным показателем
1. 
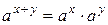
2. 
|
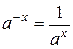
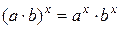
4. 
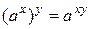
5. 
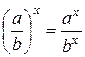
Доказательство. Пусть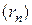 
и 
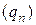– произвольные последовательности рациональных чисел, сходящиеся соответственно к
х и у.
1. Рассмотрим последовательность рациональных чисел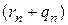 
. Для нее 
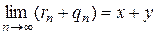. Применяя свойство степени с рациональным показателем, получаем:
.
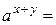
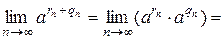
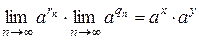2. Применяя свойства степени, получаем: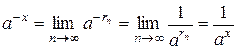 
.
3. Из свойств степени с рациональным показателем следует:
.
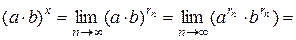
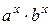4. Для рациональных значений х и у свойство 4 было установлено ранее. Рассмотрим остальные случаи.
1) Докажем равенство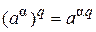 
при aÎI и q ÎQ. Пусть 
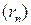–последовательность рациональных чисел, сходящаяся к a. По свойству степени с рациональным показателем имеем 
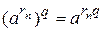(*). Найдем пределы правой и левой частей этого равенства при n ®¥.
По определению степени с иррациональным показателем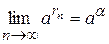 
. Отсюда по свойству непрерывности степенной функции 
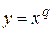получаем 
.
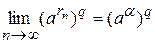Из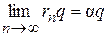 
по определению степени с иррациональным показателем следует 
.
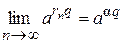Таким образом, переходя в равенстве (*) к пределу, получаем .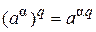
2) Докажем равенство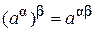 
при иррациональных значениях
a и b. Пусть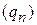 
– произвольная последовательность рациональных чисел, сходящаяся к b. По доказанному в 1) имеем: 
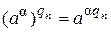(**). Перейдем к пределу при n ®¥ в равенстве (**).
Для левой части, применяя определение степени с иррациональным показателем, получаем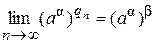 
.
Для правой части получаем: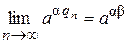 
.
Таким образом, .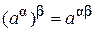
3) Аналогично доказывается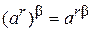 
при r ÎQ и bÎI.
Вывод: формула 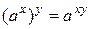справедлива при любых 
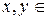R.
|
|
|
5. Опираясь на доказанные свойства, получаем:
.
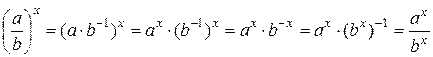Дата добавления: 2015-12-17; просмотров: 23; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!