Свойства арифметического корня
1. 
|
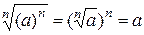
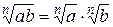
3. 
, 
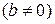
4. 
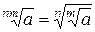
5. 
Доказательство. 1. Тождество следует непосредственно из определения арифметического корня.
2. Обозначим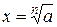 
, 
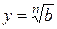. По определению корня 
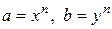. По свойствам степени с натуральным показателем 
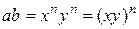. Следовательно, 
.
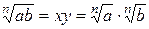3. Доказывается аналогично.
4. Обозначим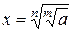 
. По определению корня 
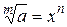, отсюда по свойствам степени 
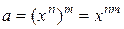. Следовательно, 
.
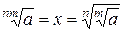5. Обозначим х =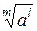 
. Тогда 
. Возведя обе части равенства в степень п, получаем 
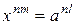. Отсюда х = 
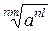. Тождество доказано.
§ 11. Понятие и свойства
степени с рациональным показателем
Пусть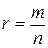 
- рациональное число, где 
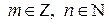, а – неотрицательное число, не обращающееся в 0 одновременно с r. При п =1 получаем 
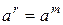– степень числа а с целым показателем.
Определение. Степенью действительного числа а с рациональным показателем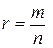 
, (т, п)=1, при 
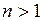называется число, определяемое формулой: 
(
).
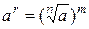Замечания.
1. , поскольку значение 00 не определено; а 0=1 для любого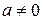 
; 0 r =0 для любого 
.
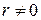2. Для отрицательного числа а степень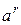 
может быть и не определена. Например, 
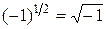не существует в R.
3. Если 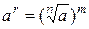существует, то равенство 
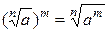выполняется при любых 
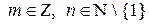. При т = 0 оно очевидно. Пусть 
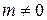. Обозначим х= 
.
1) 
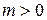. Тогда 
. Возведя обе части этого равенства в степень пт,получаем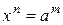 
. Следовательно, х= 
.
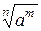2) 
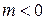. Тогда х= 1/ 
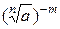, где 
. Отсюда
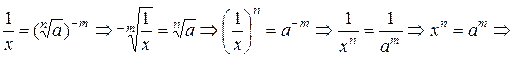х= .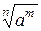
4. Если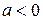 
, то в определении степени становится необходимым требование взаимной простоты чисел т и п: (т, п) = 1. Действительно, 
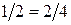, но при этом значение 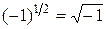не определено, а 
.
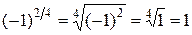Дата добавления: 2015-12-17; просмотров: 19; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!