Показательная форма комплексного числа
Показательной формой комплексного числа 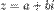 называется выражение
называется выражение

23
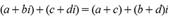
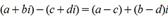
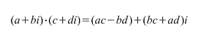
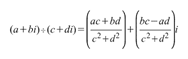
24.При возведении комплексного числа в любую целую степень модуль комплексного числа возводится в ту же степень, а аргумент умножается на показатель степени.
| (a+ i b)2= |
| =(r (cos (φ)+ i·sin (φ)))2= |
| 1. | = r 2(cos (2 φ)+ i·sin (2 φ)) |
| (a + i b) n = |
| =(r (cos (φ)+ i·sin (φ))) n = |
| 3. | = rn (cos (nφ)+ i·sin (nφ)) |
Корень 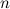 -ой степени из комплексного числа
-ой степени из комплексного числа  обозначается символом
обозначается символом  и на множестве комплексных чисел имеет ровно
и на множестве комплексных чисел имеет ровно 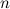 значений.
значений.
Если комплексное число  задано в тригонометрической форме:
задано в тригонометрической форме: 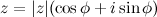 , то все значения корня
, то все значения корня 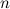 -ой степени вычисляются по формуле Муавра (Абрахам де Муавр (1667 - 1754) - английский математик):
-ой степени вычисляются по формуле Муавра (Абрахам де Муавр (1667 - 1754) - английский математик):
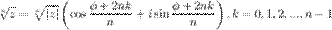
Геометрически все значения корня лежат на окружности радиуса 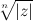 с центром в начале координат и образуют правильный
с центром в начале координат и образуют правильный 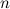 -угольник.
-угольник.
25. Квадратное уравнение с вещественными коэффициентами 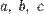 может иметь от 0 до 2 вещественных корней в зависимости от значения дискриминанта
может иметь от 0 до 2 вещественных корней в зависимости от значения дискриминанта 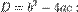
при  корней два, и они вычисляются по формуле
корней два, и они вычисляются по формуле
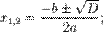 (1)
(1)
при 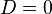 корень один (в некоторых контекстах говорят также о двух равных или совпадающих корнях), кратности 2:
корень один (в некоторых контекстах говорят также о двух равных или совпадающих корнях), кратности 2:
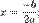
при 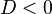 вещественных (действительных) корней нет. Существуют два комплексных корня, выражающиеся той же формулой (1) (без использования извлечения корня из отрицательного числа), либо формулой
вещественных (действительных) корней нет. Существуют два комплексных корня, выражающиеся той же формулой (1) (без использования извлечения корня из отрицательного числа), либо формулой
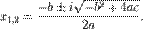
26. Функция одной переменной. Пусть задана функция у = f(x), определенная при значении аргумента, равном х 0. Дадим аргументу приращение D х, т.е. рассмотрим значение аргумента, равное x 0 + D х. Предположим, что это значение аргумента также входит в область определения данной функции. Тогда разность
D y = f(x 0 + D х) – f(x0) называется приращением функции.
|
|
|
Пусть функция y = f (x) определена в некоторой окрестности точки x 0, (включая саму эту точку).
Если существует предел отношения приращения функции Δ y = f (x 0 + Δ x) − f (x 0) к вызвавшему его приращению аргумента Δ x, когда Δ x → 0, то этот предел называется производной функции y = f (x) в точке x 0 и обозначается символом f '(x 0), т.е.
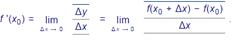
|
 27
27
28. Пусть функции 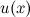 и
и  имеют производные в точке
имеют производные в точке  . Тогда
. Тогда
1. Константу можно выносить за знак производной. 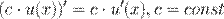
2. Производная суммы/разности.
Производная суммы/разности двух функций равна сумме/разности производных от каждой из функций. 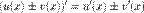
3. Производная произведения. 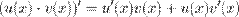
4. Производная частного. 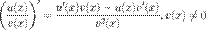
Дата добавления: 2015-12-17; просмотров: 17; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
