Элементарные функции, их классификация.
Функции, которые могут быть получены из основных элементарных функций посредством арифметических действий и образования сложных функций, называются элементарными функциями.
Элементарные функции: Трансцендентные, Алгебраические (Иррациональные, Рациональные (Целые рациональные, Дробные рациональные))
11. Функцией y=f(x) называется отображение множества X на множество Y, причем каждому элементу 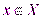 ставится в соответствие единственный элемент
ставится в соответствие единственный элемент  .
.
Числовой последовательностью x1,x2,x3…,xn называется функция xn=f(n), заданная на множестве N натуральных чисел. Обозначается 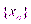
Последовательность 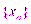 называется ограниченной, если существует такое число M>0, что для любого
называется ограниченной, если существует такое число M>0, что для любого 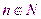 выполняется неравенство
выполняется неравенство 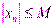 .
.
Пример: геометрическая прогрессия с основанием 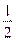 (1;
(1; 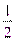 ;
; 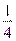 ;
; 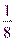 ;
;  ;
; 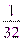 ;
; 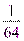 )
)
Монотонная последовательность – последовательность 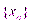 ,
, 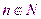 , удовлетворяющая одному из условий:
, удовлетворяющая одному из условий:
1)Для любого n выполняется неравенство 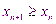 (возрастающая)
(возрастающая)
Пример: последовательность Фибоначчи (1;1;2;3;5;8;13)
2)Для любого n выполняется неравенство 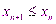 (убывающая)
(убывающая)
Пример: геометрическая прогрессия с основанием 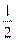 (1;
(1; 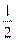 ;
; 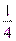 ;
; 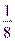 ;
; 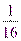 ;
; 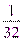 ;
; 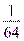 ).
).
12. В дальнейшем курсе математики понятие предела будет играть фундаментальную роль, так как с ним непосредственно связаны основные понятия математического анализа – производная, интеграл и др.Начнем с понятия предела числовой последовательности.Число a называется пределом последовательности x = { xn }, если для произвольного заранее заданного сколь угодно малого положительного числа ε найдется такое натуральное число N, что при всех n>N выполняется неравенство |xn - a| < ε.Если число a есть предел последовательности x = { xn }, то говорят, что xn стремится к a, и пишут  .Чтобы сформулировать это определение в геометрических терминах введем следующее понятие. Окрестностью точки x0 называется произвольный интервал (a, b), содержащий эту точку внутри себя. Часто рассматривается окрестность точки x0, для которой x0 является серединой, тогда x0 называется центром окрестности, а величина (b – a)/2 – радиусом окрестности.Итак, выясним, что же означает геометрически понятие предела числовой последовательности. Для этого запишем последнее неравенство из определения в виде
.Чтобы сформулировать это определение в геометрических терминах введем следующее понятие. Окрестностью точки x0 называется произвольный интервал (a, b), содержащий эту точку внутри себя. Часто рассматривается окрестность точки x0, для которой x0 является серединой, тогда x0 называется центром окрестности, а величина (b – a)/2 – радиусом окрестности.Итак, выясним, что же означает геометрически понятие предела числовой последовательности. Для этого запишем последнее неравенство из определения в виде 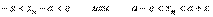 Это неравенство озна
Это неравенство озна 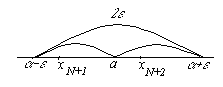 чает, что все элементы последовательности с номерами n>N должны лежать в интервале (a – ε; a + ε).Следовательно, постоянное число a есть предел числовой последовательности { xn }, если для любой малой окрестности с центром в точке a радиуса ε (ε – окрестности точки a) найдется такой элемент последовательности с номером N, что все последующие элементыс номерами n>N будут находиться внутри этой окрестности. Сходящаяся последовательность — это последовательность элементов множества X, имеющая предел в этом множестве. Расходящаяся последовательность — это последовательность, не являющаяся сходящейся.
чает, что все элементы последовательности с номерами n>N должны лежать в интервале (a – ε; a + ε).Следовательно, постоянное число a есть предел числовой последовательности { xn }, если для любой малой окрестности с центром в точке a радиуса ε (ε – окрестности точки a) найдется такой элемент последовательности с номером N, что все последующие элементыс номерами n>N будут находиться внутри этой окрестности. Сходящаяся последовательность — это последовательность элементов множества X, имеющая предел в этом множестве. Расходящаяся последовательность — это последовательность, не являющаяся сходящейся.
|
|
|
|
|
|
13Определение. Ряды, все члены которых имеют одинаковые знаки, называются знакопостоянными. Для определенности, если это не будет оговорено особо, мы будем рассматривать ряды с положительными членами или знакоположительные ряды: P, Q, …: pn> 0, qn> 0,
Очевидно, что последовательность частичных сумм знакоположительных рядов монотонно возрастает: P 1 <P 2 < … <Pn<Pn+ 1 < …. Следовательно, верна
Теорема. Для сходимости знакоположительного ряда необходимо и достаточно, чтобы последовательность его частичных сумм была ограничена.
14 Последовательность 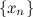 называется бесконечно малой последовательностью (б.м.п.),если для любого
называется бесконечно малой последовательностью (б.м.п.),если для любого 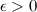 существует номер
существует номер 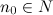 такой, что для любого
такой, что для любого 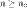 выполняется неравенство:
выполняется неравенство: 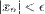 Последовательность
Последовательность 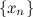 называется бесконечно большой (б.б.п.), если для любого
называется бесконечно большой (б.б.п.), если для любого 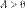 существует номер
существует номер 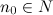 такой, что для любого
такой, что для любого 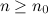 выполняется неравенство:
выполняется неравенство: 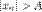 Основные свойства б.м. и б.б. последовательностей 1° Сумма б.м. последовательностей есть б.м.п. 2.Произведение ограниченной последовательности и б.м. есть б.м.п. 3° Если
Основные свойства б.м. и б.б. последовательностей 1° Сумма б.м. последовательностей есть б.м.п. 2.Произведение ограниченной последовательности и б.м. есть б.м.п. 3° Если 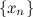 - б.м.п., то
- б.м.п., то 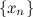 - ограниченная последовательность.4° Произведение б.м.п. есть последовательность б.м.5° Если
- ограниченная последовательность.4° Произведение б.м.п. есть последовательность б.м.5° Если 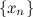 - б.м.п. и
- б.м.п. и 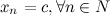 , то
, то 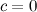 , т.е.
, т.е. 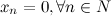 6° Если
6° Если 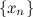 - б.м.п. и
- б.м.п. и 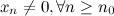 , то последовательность
, то последовательность 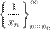 - б.б.п.7° Если
- б.б.п.7° Если 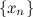 - б.б.п., то
- б.б.п., то 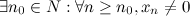 и последовательность
и последовательность 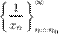 - б.м.п.
- б.м.п.
|
|
|
15-------
16 Функция  называется бесконечно малой при
называется бесконечно малой при 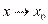 , если
, если 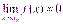 .Функция
.Функция 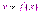 называется бесконечно большой при
называется бесконечно большой при 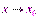 , если для любого положительного числа
, если для любого положительного числа 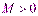 существует такое число
существует такое число  , что для всех
, что для всех  , удовлетворяющих неравенству
, удовлетворяющих неравенству 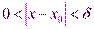 , выполняется неравенство
, выполняется неравенство 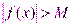 . Записывается:. Свойства бесконечно малых функций: 1)Алгебраическая сумма конечного числа бесконечно малых функций есть бесконечно малая функция.
. Записывается:. Свойства бесконечно малых функций: 1)Алгебраическая сумма конечного числа бесконечно малых функций есть бесконечно малая функция.
2)Произведение ограниченной функции на бесконечно малую функцию есть функция бесконечно малая.
3)Произведение двух бесконечно малых функций есть функция бесконечно малая.
4)Произведение бесконечно малой функции на число есть функция бесконечно малая.
5)Частное от деления бесконечно малой функции на функцию, имеющую отличный от нуля предел, есть функция бесконечно малая.
Теорема о связи между бесконечно большой и бесконечно малой функциями: Если функция 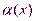 - функция бесконечно малая (
- функция бесконечно малая (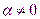 ), то функция
), то функция 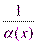 есть бесконечно большая функция и наоборот.Доказательство: Пусть
есть бесконечно большая функция и наоборот.Доказательство: Пусть 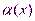 - бесконечно малая функция при
- бесконечно малая функция при 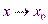 , т.е.
, т.е. 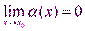 . Тогда для любого числа
. Тогда для любого числа 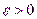 существует такое число
существует такое число 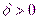 , что для всех
, что для всех 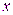 , удовлетворяющих неравенству
, удовлетворяющих неравенству 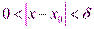 , выполняется неравенство
, выполняется неравенство  , т.е.
, т.е. 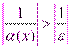 , т.е.
, т.е. 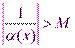 , где
, где 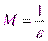 . А из этого следует, что функция
. А из этого следует, что функция 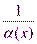 - бесконечно большая.
- бесконечно большая.
|
|
|
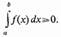 17 До сих пор мы рассматривали свойства интегралов, выражаемые равенствами; перейдем теперь к таким, которые выражаются неравенствами.
17 До сих пор мы рассматривали свойства интегралов, выражаемые равенствами; перейдем теперь к таким, которые выражаются неравенствами.
5°. Если функция  интегрируемая в промежутке
интегрируемая в промежутке  неотрицательна и
неотрицательна и 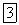 то
то
Доказательство очевидно.Труднее доказать более точный результат:Если функция  интегрируемая в промежутке
интегрируемая в промежутке 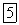 положительна и
положительна и  , то
, то 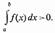
18 Первый замечательный предел имеет вид: 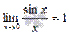 На практике чаще встречаются модификации первого замечательного предела в виде
На практике чаще встречаются модификации первого замечательного предела в виде
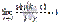 где, k – коэффициент.Пояснение:
где, k – коэффициент.Пояснение: 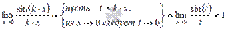 Следствия первого замечательного предела:
Следствия первого замечательного предела:
1. 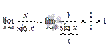 2
2 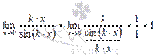
19Второй замечательный предел имеет вид: 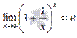 или в другой записи
или в другой записи 
В случае второго замечательного предела имеем дело с неопределенностью вида единица в степени бесконечность  .Разберем несколько примеров нахождения предела по второму замечательному пределу с подробным оприсанием решения.
.Разберем несколько примеров нахождения предела по второму замечательному пределу с подробным оприсанием решения.
20. Исследование функции на непрерывность связано с нахождением односторонних пределов функции. Так что рекомендуем ознакомится с разделом Предел функции, основные определения и понятия, прежде чем двигаться дальше. Определение непрерывности функции в точке.Функция f(x) называется непрерывной в точке 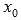 , если предел слева равен пределу справа и совпадает со значением функции в точке
, если предел слева равен пределу справа и совпадает со значением функции в точке 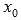 , то есть
, то есть 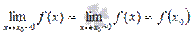 .
.
Следствие. ЗНАЧЕНИЕ ПРЕДЕЛА ФУНКЦИИ В ТОЧКАХ НЕПРЕРЫВНОСТИ СОВПАДАЕТ СО ЗНАЧЕНИЕМ ФУНКЦИИ В ЭТИХ ТОЧКАХ.
21. Непрерывность функции на отрезке. Свойства функций, непрерывных на отрезке
Определение 4. Функция называется непрерывной на отрезке, если она непрерывна в каждой точке этого отрезка (в точке a непрерывна справа, т.е., а в точке b непрерывна слева, т. е.).
Все основные элементарные функции непрерывны в области их определения.
Свойства функций, непрерывных на отрезке:
1) Если функция непрерывна на отрезке, то она ограничена на этом отрезке (первая теорема Вейерштрасса).
2) Если функция непрерывна на отрезке, то на этом отрезке она достигает своего наименьшего значения и наибольшего значения (вторая теорема Вейерштрасса) (см. рис. 2).
3) Если функция непрерывна на отрезке и на его концах принимает значения разных знаков, то внутри отрезка существует хотя бы одна точка такая, что (теорема Больцано-Коши).
22. Комплексным числом называется выражение вида a + ib, где a и b – любые действительные числа, i – некоторый символ, который называется мнимой единицей. Часто используют символическую запись 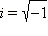 .
.
Комплексные числа часто обозначают одной буквой, например, z = a + ib. Действительное число a называется действительной частью комплексного числа z, действительная часть обозначается a = Re z. Действительное число b называется мнимой частью комплексного числа z, мнимая часть обозначается b = Im z.
Сопряженным (или комплексно сопряженным) числом к комплепрксному числу называется число.
Длина вектора, изображающего комплексное число, называется модулем комплексного числа. Модуль любого комплексного числа, не равного нулю, есть положительное число. Модуль комплексного числа a + b·i обозначается |a + b·i|, а также буквой r. Из чертежа видно, что:
r = | a + b·i | =
| a 2+ b 2 |
Модуль действительного числа, совпадает с его абсолютным значением. Сопряженные комплексные числа a + b · i и a - b · i имеют один и тотже модуль.

Дата добавления: 2015-12-17; просмотров: 18; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
