Геометрии движения по эллипсу
Коническим сечением называется кривая, по которой пересекает круговой конус произвольная плоскость, не проходящая через его вершину. Каждое коническое сечение, кроме окружности, представляет собой геометрическое место точек плоскости, отношение расстояний которых от некоторой точки F (фокус) и некоторой прямой δ (директриса) постоянно и равно е (эксцентриситет) (рис.17) [33].
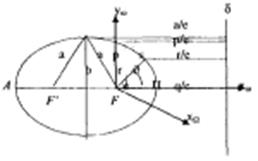
Рис. 17. Геометрия движения по эллипсу
В этом фокусе находится притягивающее тело. Второй фокус F' эллипса будем называть пустым. Ближайшая к фокусу F точка эллипса П называется перигеем (или перицентром в общем случае), а наиболее удаленная от этого фокуса точка эллипса А называется линией апогеем (апоцентром). Прямая, проходящая через перицентр и апоцентр называется линией апсид. Расстояние от фокуса до перицентра называется перигейным расстоянием q, а от фокуса до апоцентра – апогейным расстоянием Q. Длина перпендикуляра к линии апсид от фокуса до точки эллипса называется фокальным параметром р. Угол между линией апсид и направлением на точку s (спутник) эллипса называется истинной аномалией υ. Угол между направлением на восходящий узел и на спутник называется аргументом широты u.
Непосредственно из рисунка видно, что
p = r(1 + ecosσ) (3.34)
откуда
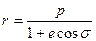(3.35)
При σ = 0
r = q,
и
p = q(1 + e) (3.36)
Имея к виду второе определение эллипса (сумма расстояний от фокусов до текущей точки эллипса есть величина постоянная и равна удвоенному значению большой полуоси 2а), можно записать:
|
|
|
a/е = а + q/e.
Отсюда
q = a(1 – e) (3.37)
И тогда
р = а(1 - е2). (3.38)
Очевидно также
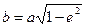(3.39)
b - малая полуось.
Сравнивая (3.35) с (3.33), замечаем, что
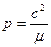(3.40)
и
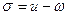(3.41)
Угол ω называется аргументом перицентра; это угол между направлением на восходящий учел орбиты спутника и направлением на перицентр орбиты.
Из интегрирования дифференциальных уравнений движения можно вывести и третий закон Кеплера. Если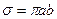 
- площадь эллипса, то удвоенная секториальная скорость равна [15]:
(13.42)
где Т - период обращения.
Так как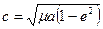 
, а 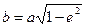,то из (3.42) найдем формулу
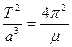(3.43)
представляющую собой математическое выражение третьего закона Кеплера: отношение квадрата периода обращения к кубу большой полуоси - величина постоянная. В (3.43) μ представляет собой произведение гравитационной постоянной на сумму масс притягивающего и притягиваемого тел. В этом и состоит уточнение Ньютона третьего закона Кеплера.
Величину 
называют средним движением по эллиптической орбите.
Уравнение Кеплера
Рис. 18. Истинная и эксцентрическая аномалии
Введем вначале эксцентрическую аномалию Е (рис. 18). Для этого из центра эллипса опишем окружность радиусом большой полуоси. Из текущего положения спутника на орбите опустим перпендикуляр на линию апсид и продолжим его до пересечения с окружностью. Угол между линией апсид и прямой OS' и называется эксцентрической аномалией.
|
|
|
Введем плоскую правую прямоугольную систему координат, начало которой поместим в непустой фокус эллипса, а ось абсцисс направим в перицентр эллиптической орбиты.
Прямоугольные координаты текущих точек эллипса в этой орбитальной системе координат через истинную аномалию выражаются просто
xω = rcosσ (3.44)
yω = rsinσ (3.45)
Используя уравнение орбиты (3.35), можно написать
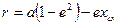(3.46)
Выразим теперь прямоугольные координаты текущих точек эллипса через эксцентрическую аномалию. Непосредственно из рис.18 видно, что выражение для абсциссы есть:
(3.47)
Подставив (3.47) в (3.46), получим
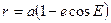(3.48)
Теперь можно найти выражение для орбиты
(3.49)
Нам потребуются также скорости изменения координат, выражения для которых получим дифференцированием (3 47) и (3.49).
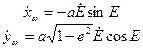(3.50)
В интеграле площадей
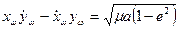(3.51)
сделаем заменыс помощыо (3.47), (3.49), (3.50). Тогда (3.51) запишем в виде:
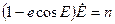(3.52)
Интегрируя последнее выражение, получаем уравнение Кеплера:
E = M + esinE, (3.53)
где
М = n(i - τ) - средняя аномалия,
|
|
|
τ - произвольная постоянная интегрирования, которую называют моментом прохождения через перицентр.
Уравнение Кеплера решается методом последовательных приближений
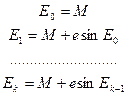(3.54)
Уравнение Кеплера связывает эксцентрическую и среднюю аномалии. Выведем формулу, связывающую истинную и эксцентрическую аномалии. Из сравнения (3.44) и (3.47) можно записать:
rcosσ = a(cosЕ - е). (3.55)
Сначала вычитая, а потом складывал почленно (3.48) и (3.55), получим
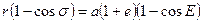(3.56)
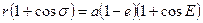(3.57)
Откуда, разделив (3.56) на (3.57), имеем
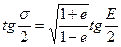(3.58)
Полезной в некоторых случаях может оказаться также формула, выведенная Брукке и Чевода:
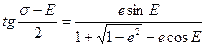(3.59)
Дата добавления: 2016-01-05; просмотров: 107; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!