Дифференциальные уравнения движения ИСЗ в прямоугольных координатах
При выводе дифференциальных уравнений движения будем считать Землю и спутник в виде материальных точек соответствующей массы, которые движутся друг относительно друга лишь под действием сил взаимного притяжения. Такое движение называется невозмущенным.
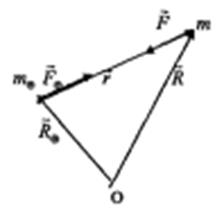
Рис. 15.Векторы,определяющие положение двух тел
На рис.15 сила притяжения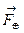 
, действующая на Землю, масса которой, 
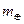направлена вдоль вектора 
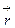г в сторону спутника, масса которого m, в то время как сила 
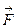, приложенная к m, действует в противоположном направлении.
На основании третьего закона Ньютона
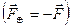и закона всемирного тяготения можно записать выражения для сил, действующих на Землю и на спутник [26]:
.
Будем рассматривать движение Земли и спутника в не вращающейся прямоугольной системе координат, начало которой совместим с некоторой произвольной фиксированной точкой О. В этой системе координат положения Земли и спутника будут задаваться векторами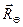 
и 
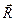, направленными из точки О к телам с массами 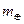и m соответственно. Система координат, связанная с точкой О, будет инерциальной и, значит, в этой системе координат будет справедлив второй закон Ньютона. Следовательно, уравнения движения тел относительно точки О под действием сил взаимного притяжения принимают вид:
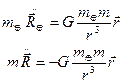(3.1)
Необходимо отметить, что массы в левых и правых частях равенств (3.1) выражают различные свойства теп. Массы в левых частях характеризуют инерционные свойства тел и называются инертными массами. Массы в правых частях характеризуют способность тел притягивать другие тела и притягиваться ими называются тяжелыми или гравитационными массами. Существует, однако, фундаментальный закон природы, в соответствии с которым инертная и тяжёлая массы пропорциональны друг другу. При надлежащем выборе единиц измерения эти массы будут просто тождественны Эквивалентность инертной и тяжёлой масс проверял еще сам И. Ньютон, измеряя периоды колебаний математического маятника. С помощью крутильных весов Л. Этвеш доказал справедливость принципа эквивалентности с точностью до 10-8; Р. Дикке довел точность до 10-10;
|
|
|
В. Е. Брагинский - до 10-12. Вот почему для масс в левых и правых частях (3.1) использованы одни и те же обозначения.
Сложим почленно (3.1) и после двукратного интегрирования получим:
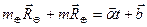
где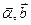 
- произвольные постоянные интегрирования.
Введя радиус-вектор центра масс системы
, 
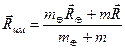
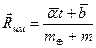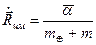(32)
Из (3.2) следует, что центр масс системы движется прямолинейно и равномерно.
Вычитая первое уравнение из второго в (3.1) и учитывая, что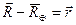 
, получим дифференциальные уравнения относительного невозмущенного движения в векторной форме:
(3.3)
|
|
|
где
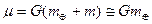- геоцентрическая гравитационная постоянная.
Масса спутника пренебрежимо мала по сравнению с массой Земли, поэтому центр масс системы практически совпадает с центром масс Земли и, следовательно, геоцентрическую равноденственную систему координат, отнесённую к определённой эпохе, например, к эпохе 2000.0 года, можно считать инерциальной. В координатной форме уравнении движения выглядят:
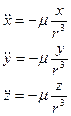(3.4)
Введем функцию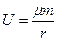 
, которую называют силовой функцией в силу того, что частные производные от неё по координатам равны проекциям силы на соответствующие оси координат. Заметим также, что силовая функция, взятая с обратным знаком, численно равна потенциальной энергии. Тогда уравнения движения (3.4) можно записать в виде:
(3.5)
Еcли ввести кинетическую энергию Т, выражаемую формулой
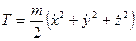(3.6)
то левые части уравнений движения в (3.5) можно записать в виде:
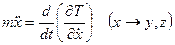(3.7)
И тогда уравнения движения можно представить следующим образом:
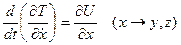(3.8)
Введя теперь так называемую функцию Лагранжа, представляющую собой разность кинетической и потенциальной энергий L=- Т + U и имея в виду, что U не зависит от скоростей, а Т не зависит от координат, уравнения движения можно записать:
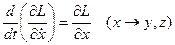(3.9)
Ковариантная форма уравнений движения
|
|
|
Форма записи дифференциальных уравнений движения называется ковариантной, если она не зависит от вида используемых систем координат. Для вывода ковариантной формы дифференциальных уравнений движения выразим прямоугольные координаты точки (спутника) х, y, z в виде функций от п произвольных координат q (например, полярных, цилиндрических или каких-нибудь других координат) и времени t. Эти произвольные координаты называют по предложению Лагранжа обобщенными координатами, а их производные по времени - обобщёнными скоростями
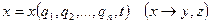
Тогда имеет место соотношение:
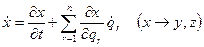
Для любого q (например, для q1) получаем
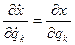
Покажем, что форма дифференциальных уравнений движения (3.9) не изменится при использовании вместо прямоугольных любых других координат. Для этого дифференцируем (3.6) частный образом по обобщённым координатам и обобщенным скоростям:
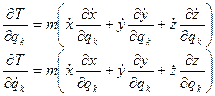
Тогда
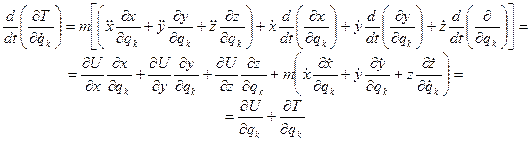
Вводя опять функцию Лагранжа L=T+U и имея в виду, что U не зависят от обобщённых скоростей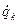 
, уравнения движения можно записать:
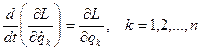(3.10)
Ковариантная форма уравнений движения (3.10) называется также уравнениями Лагранжа второго рода или уравнениями Эйлера - Лагранжа. Имея в виду, что частная производная от функции Лагранжа по обобщённым координатам представляет собой обобщенную силу, а частая производная от функции Лагранжа по обобщённым скоростям - обобщенный импульс, то уравнения (3.10) есть не что иное, как математическое выражение в общем виде второго закона Ньютона.
|
|
|
Дата добавления: 2016-01-05; просмотров: 53; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!