Интегрирование дифференциальных уравнений не возмущённого движения
Уравнения невозмущённого движения представляют собой систему трёх дифференциальных уравнений второго порядка. Решение этой системы должно дать шесть интегралов и шесть произвольных постоянных. Эти шесть интегралов, называемые в небесной механике первыми интегралами, представляют собой функции координат и скоростей, не изменяющиеся в процессе движения [9].
Интегралы площадей
Умножив уравнения движения 
— векторно на 
, получим уравнения
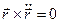
которые легко интегрируются:
(3.11)
Компонентами вектора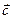 
являются произвольные постоянные интегрирования. Заметим, что (3.11) выражает постоянство кинетического момента. Записав векторное произведение в левой части (3.11) в виде определителя, а правую часть представив в координатной форме
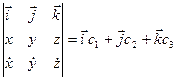(3.12)
получим выражения для постоянных интегралов:
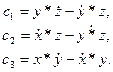(3.13)
Умножая теперь первое уравнение на х, второе - на у, третье - на z, и суммируя результаты, получим уравнение
с1*x + с2*у + с3*z = 0, (3.14)
представляющее собой уравнение плоскости, проходящей через начало координат.
Это означает, что невозмущённая орбита ИСЗ лежит в плоскости, проходящей через центр масс Земли. Уравнение (3.14) можно записать и в векторной форме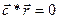 
, из которого следует, что плоскость орбиты перпендикулярна вектору 
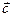. Так как невозмущенная орбита является плоской кривой, то уравнения движения удобно записать в геоцентрической орбитальной системе координат хΩуΩzΩ (рис.16).
|
|
|
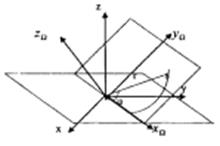
Рис. 16. Геоцентрические средняя равноденственная и орбитальная системы координат
Ось абсцисс этой системы координат направлена по линии пересечения плоскости орбиты с плоскостью экватора, ось аппликат направлена по нормали к плоскости орбиты, а ось ординат дополняет систему до правой тройки векторов:
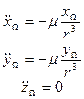(3.14)
Тогда (3.12) примет вид:
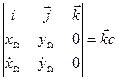
и вместо трех интегралов (3.13) получим один интеграл
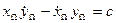(3.16)
Выразим прямоугольные координаты xΩ, yΩ через полярные r, u.
xΩ = r*cosu
yΩ = r*sinu
Тогда выражение для с будет:
(3 17)
Левая часть (3.17) представляет собой удвоенную секториальную скорость. Секториальной скоростью называется площадь, заметаемая радиус-вектором в единицу времени. Таким образом, можно заключить, что в процессе невозмущенного движения секториальная скорость остается неизменной величиной, и (3.17) представляет собой математическое выражение второго закона Кеплера, в соответствии с которым радиус-вектор за одинаковые промежутки времени заметает одинаковые площади. В связи с этим интегралы (3.13) и называются интегралами площадей.
Интеграл энергии
Умножим уравнения движения скалярно на 
:
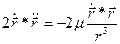(3.18)
Учитывая, что
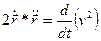
и
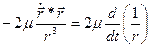
произведем замены в левой и правой частях (3.18) и после интегрирования, найдем:
|
|
|
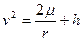(3.19)
Здесь v – орбитальная скорость, h – новая произвольная постоянная, называемая постоянной энергии.
Найденный интеграл представляет собой закон сохранения энергии в системе Земли – ИСЗ, поэтому его и называют интегралом энергии.
Интегралы Лапласа
Если найти такую функцию, вторая производная ко времени от которой по форме имела бы такой же вид, что и вторая производная по времени от радиуса-вектора в уравнениях невозмущённого движения ИСЗ , то система проинтегрируется методом разделения переменных. Оказывается, что такой функцией является функция D.
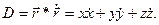(3.20)
Запишем первую и вторую производные по времени от функции D.
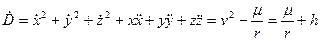(3.21)
(3.22)
Сравнивая (3.22) с уравнениями невозмущенного движения, можно записать новые дифференциальные уравнения
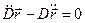(3.23)
интегрируя которые получим:
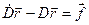(3.24)
где компоненты вектора 
- произвольные постоянные интегрирования, которые называются постоянными Лапласа.
Уравнения (3.24) можно представить в координатной форме:
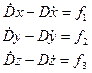(3.25)
Эти уравнения называются интегралами Лапласа.
Итак, в результате интегрирования уравнений невозмущенного движения найдены семь первых интегралов - три интеграла площадей, интеграл энергии, три интеграла Лапласа, т.е. как будто даже больше, чем надо, поскольку общий интеграл системы должен состоять из шести независимых интегралов. Однако найденные семь интегралов не могут составить общего интеграла системы, так как ни один из этих интегралов не содержит времени, и эти семь интегралов не являются независимыми.
|
|
|
Найдем два тождественных соотношения, существующих между этими интегралами.
Для этого интегралы площадей
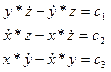
умножим на интегралы Лапласа
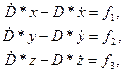
и результаты просуммируем.
Тогда получим;
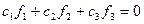(3.26)
или в векторной форме
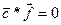(3.27)
Из найденного выражения (3 27) следует, что вектор Лапласа лежит в плоскости орбиты, поскольку вектор площадей перпендикулярен плоскости орбиты.
Для вывода второго соотношения возведем в квадрат интегралы площадей и интегралы Лапласа. В результате получим:
(3.28)
Из (3.28) после несложных преобразований следует второе соотношение
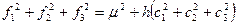(3.24)
Интеграл орбиты
Запишем уравнения движения в ковариантной форме:
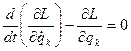
Так как невозмущенное движение представляет собой плоскую кривую, то в качестве обобщенных координат удобно использовать полярные координаты
q1 = r, q2 = u
Записав квадрат орбитальной скорости в виде
|
|
|
функция Лапласа будет:
(3.30)
Взяв необходимые производные от функции Лагранжа
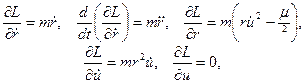
уравнения движения запишутся в виде системы из двух уравнений:
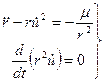(3.31)
Второе уравнение системы (3.31) интегрируется сразу и дает уже известным интеграл площадей:
Для удобства интегрирования первого уравнения системы (3.31) воспользуемся правилом дифференцирования сложной функции и сделаем подставку Бине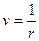 
[32]. Тогда первую и вторую производные по времени от r можно представить в виде:
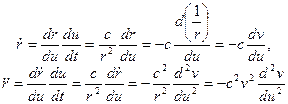
В результате таких преобразований первое уравнение в (3.31) упрощается
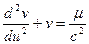(3.32)
и легко интегрируется. В результате интегрирования (3.32) и обратного перехода к r получим:
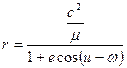(3.33)
где
е и ω – новые произвольные постоянные интегрирования.
Полученный интеграл называется интегралом орбиты. Уравнение (3.33) представляет собой уравнение конического сечения, а это означает, что орбита может быть окружностью, эллипсом, параболой или гиперболой. Следовательно, (3.33) является обобщённым математическим выражением первого закона Кеплера.
Дата добавления: 2016-01-05; просмотров: 36; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!