Уравнивание триангуляции коррелатным способом.

Условные уравнения. Число независимых условий.

       Уравнивание коррелатным способом выполняют по углам или – более строго – по направлениям. Условные уравнения разделяют на угловые и синусные. Угловыми называют линейные условия, имеющие коэффициенты ±1 и 0. Синусными называют нелинейные условные уравнения, в которых содержатся синусы. В триангуляции после устранения невязок угловых условий дирекционный угол любой стороны сети определяется однозначно независимо от пути его передачи от исходных дирекционных углов.

       В триангуляции имеются следующие виды угловых условий.

       Условия фигур возникают в треугольниках и многоугольниках. В плоском треугольнике (рис.1а),

1 + 2 + 3 – 180⁰ = ω

 где 1, 2, 3 – измеренные значения углов треугольника; ω – невязка в треугольнике. При уравнивании к углам J определяют поправки (J) и получают

1+ (1) + 2 + (2) + 3 + (3) – 180⁰ = 0.

 

Рис.1

Из сравнения этих выражений находят условие фигур

(1) + (2) + (3) + ω = 0.

При уравнивании направлений для треугольника условное уравнение фигур имеет вид (рис1.б)

-(1) + (2) – (3) + (4) – (5) + (6) + ω = 0 ,

где ω = [2-1] + {4-3] + [6-5] – 180⁰.

       Условия горизонта возникают на пунктах, на которых в уравнивание включены все углы, образуемые смежными направлениями, сумма этих углов равна 360⁰, т.е.

(1) + (2) + …+(N) + ω = 0.

При уравнивании по направлениям условий горизонта не возникает.

Условия исходных дирекционных углов возникают при вставке цепочки треугольников в угол или между исходными сторонами и состоят в том, что сумма уравненных углов должна равняться величине жесткого угла или дирекционный угол стороны СД (рис.1.в) должен равняться его вычисленному значению от исходного дирекционного угла стороны АВ с использованием уравненных значений углов треугольников.

На рис.1.а α_ВС + 6 + 3 – α_ВА = ω.

После введения поправок и преобразований получаем условное уравнение

(3) + (6) + ω = 0 .

Для сети на рис.1.в.

α_АВ ± 180⁰ – С₁ ± 180⁰ + С₂ ± 180⁰ – С₃ – α_СД = ω .                           (1)

       После введения поправок и преобразований находим условное уравнение

– (С₁) + (С₂ ) – (С₃ ) + ω = 0 .

       Если дирекционные углы α_АВ и α_СД (рис.1.в) получены из измерений и поправки (α_АВ) и (α_СД) в их значениях определяют из уравнивания сети, то условное уравнение дирекционных углов в этом случае имеет вид

– (С₁) + (С₂ ) – (С₃ ) + (α_АВ) - (α_СД) + ω = 0 ,

где ω определяют по формуле (1).

       Синусные условия состоят из полюсных, базисных и координатных; их учет необходим для однозначного определения длины любой стороны сети независимо от пути ее определения от исходных сторон. Координатные условия обеспечивают однозначное получение координат любого пункта сети.

       Полюсные условия возникают в центральных системах и геодезических четырехугольниках, так как в этих фигурах одна сторона является избыточной. На рис.2 с учетом замены отношения сторон отношением синусов противолежащих им углов имеем

.

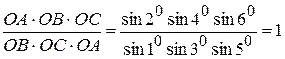       Учитывая J⁰ = J + (J) и малую величину поправок (J), получаем

.

С учетом этого

 .

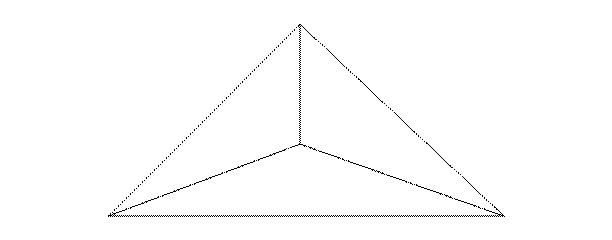
Рис.2

После преобразований, принимая во внимание  и отбрасывая величины второго порядка малости, имеем

 .

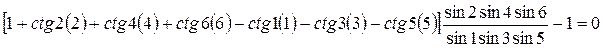       Выражая поправки в угловых секундах, находим

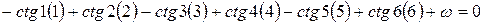 ,      (2)

где

.

       Полюсное условное уравнение (2) получено для уравнивания углов. При уравнивании направлений поправки в углы выражают через поправки в направления. Учитывая, что угол равен разности направлений, на рис.2 имеем 1 = 2 – 1 , 2 = 6 – 5 и т.д.; значение -ctg1(1) = ctg(2-1)(1) – ctg(2-1)(2) и т.п. В результате, после приведения подобных членов при одноименных поправках имеем

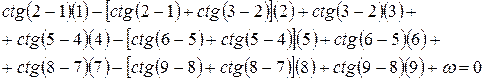
где

.

 

       Базисные условия. На рис.1.а по теореме синусов

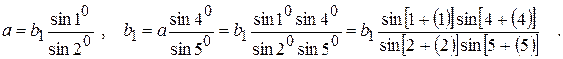
       Выполняя преобразования, аналогичные сделанным при выводе полюсного условия, находим

 ,

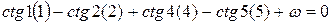где   .

       На рис.1.в аналогичным способом получаем

 ,

где   .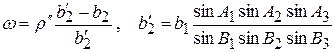

       Если одна или обе исходные стороны b₁ и b₂  измерены и поправки (b₁)и (b₂) в их длины определяют из уравнивания, то приведенное выше базисное условное уравнение дополняют поправками с коэффициентами при них, т.е. к левой части прибавляют

  .

       Условные уравнения абсцисс и ординат возникают, если в сети триангуляции имеются группы исходных пунктов, удаленные одна от другой не менее чем на две определяемые стороны.

Рис.3

На рис.3 одна группа состоит из смежных пунктов А и В, а вторая – из пункта Д. При составлении условных уравнений в цепочке треугольников, соединяющей ближайшие пункты групп, намечают ходовую линию (на рис.3 – АСЕД), проходящую через вершины промежуточных углов треугольников. В уравненной сети должны соблюдаться равенства

.

       Значение приращений координат

 

,

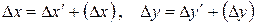где Δx’, Δy’ вычисляют с использованием измеренных углов А, В, С.

       С учетом этого

                             (3)

где .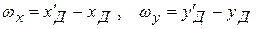

       Для получения уравнения абсцисс выразим поправки (Δx) через поправки в измеренные углы. Учитывая 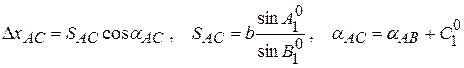  и отбрасывая в процессе вывода величины второго и более высокого порядка малости, и учитывая 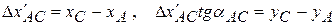, имеем

 .

Аналогично получаем (Δx_СЕ) и (Δx_ЕД).

       Суммируя полученные значения и подставляя сумму в первую из формул (3), находим условие абсцисс

.

       Аналогично получим условие ординат

,

где  x’ _n , y’ _n – координаты конечного пункта, вычисленные по измеренным углам от начального пункта; x_n , y_n – твердые координаты конечного пункта; x, y – координаты текущих точек по ходовой линии.

       При уравнивании по направлениям поправки в углы выражают через поправки в измеренные направления.

       Условия проекций  возникают, если в сети имеется длинная диагональ, соединяющая вершины несмежных треугольников (рис.4) и измерены один угол (β₁ или β₂) или два (β₁ и β₂) избыточных угла. Приняв диагональ АД за ось абсцисс, а перпендикулярное ей направление – за ось ординат, можно вычислить дирекционные углы линий АВ, ВС, СД (дирекционный угол линии АД равен нулю) и приращения ординат. В итоге получим

,

где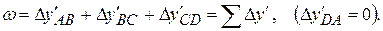

       Условия проекций усложняют уравнительные вычисления, практически не повышая точности сети, поэтому при проектировании сети нужно избегать возникновения этих условий.

       Число независимых условных уравнений. Согласно методу наименьших квадратов, общее число (r) условных уравнений r = n – k, где n – число всех измеренных величин; k – их необходимое количество. При уравнивании углов k = 2g, где g -  число определяемых пунктов, т.е. r = n – 2g.

       При уравнивании направлений общее число условий равно их значению, полученному по формуле для углов, минус число условий горизонта.

       Подсчитывают число r_y  угловых условий (при уравнивании углов)

r_y = n^’ – k^’ ,

 

Рис.4

           

где n^’ – число измеренных углов и геодезических азимутов* k^’ – число определяемых сторон. Число различных видов угловых условных уравнений подсчитывают в такой последовательности:

1) определяют число  условий горизонта r_r,  равное числу центральных систем; 2) находят число условий дирекционных углов r_a, равное числу всех – жестких и нежестких – дирекционных углов без одного; 3) число условий треугольников (фигур) r_ф, равное оставшемуся числу угловых условий.

       Синусные условия (их общее число r_c = r – r_y) подсчитывают в следующем порядке; 1) получают число координатных условий r_k = 2(n – 1), где n -  число изолированных систем исходных пунктов; 2) определяют число базисных условий, равное числу Б базисных сторон – жестких и нежестких – без одной (r_б = Б – 1); 3) число r_п полюсных условных уравнений равно оставшемуся числу синусных условий, т.е. r_п =  r_c  - r_k – r_б; кроме того, число полюсных условий равно числу центральных систем и геодезических четырехугольников.

       Пример. Определить число и виды условных уравнений для сети, изображенной на рис.5. При уравнивании углов общее число условий r = n – 2g = 22 – 10 = 12, угловых условий r_y = n^’ – k^’ = 22 – 13 = 9. Из них число условий горизонта r_r = 1, условий дирекционных углов r_α = 0, условий фигур r_ф = 9 – 1 = 8 - по три условия в двух геодезических четырехугольниках плюс два условия в двух треугольниках. Число синусных условий r_c = r – r_y = 12 – 9 = 3, из них: полюсных условий k_n = 3 (одно в центральной системе и два в двух геодезических четырехугольниках), координатные и базисные условия отсутствуют.

 

Рис.5

 

 

Оценка точности функций

        В коррелатном способе составляют функцию F = f( x₁, x₂, …, x_n). После ее разложения в ряд находят

,

 

где ; свободный член  - результаты измерений; v_i – поправки.

       Среднюю квадратическую ошибку функции определяют по формуле

 ,

где  ; r – число избыточных измерений.

 

---

Дата добавления: 2022-01-22; просмотров: 125; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!