Основні властивості визначників
| 1) | Транспонування не змінює значення визначника. |
Наприклад, 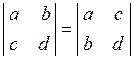 . (Ця властивість вказує на рівноправність рядків та стовпців з визначника.) . (Ця властивість вказує на рівноправність рядків та стовпців з визначника.)
| |
| 2) | Якщо всі елементи рядка (або стовпця) визначника дорівнюють нулю, тоді визначник дорівнює нулю. |
Наприклад,  . .
| |
| 3) | Якщо визначник має два однакові рядки (або стовпці), тоді він дорівнює нулю. |
Наприклад, 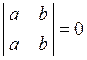 . .
| |
| 4) | Якщо визначник має два пропорційні рядки (або стовпці), тоді він дорівнює нулю. |
Наприклад, 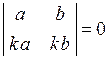 . .
| |
| 5) | Якщо у визначнику поміняти місцями два рядки (або стовпці), то знак визначника зміниться на протилежний. |
Наприклад, 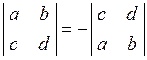 . .
| |
| 6) | Спільний множник рядка (або стовпця) можна винести за знак визначника. |
Наприклад,  . .
| |
| 7) | Якщо до рядка (або стовпця) визначника додати його інший рядок (або стовпець), помножений на довільне число, то значення визначника не зміниться. |
Наприклад, 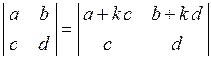 . .
| |
| 8) | Якщо всі елементи рядка (або стовпця) визначника можна подати у вигляді суми двох доданків, то цей визначник дорівнює сумі визначників, які визначаються цими доданками. |
Наприклад, 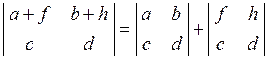 . .
|
Доведення властивостей визначників можна проілюструвати на прикладі визначника другого порядку, визначивши ліву та праву частину у наведених вище співвідношеннях.
Використовуючи властивості визначників і теорему Лапласа, можна легко обчислювати визначники високих порядків.
|
|
|
| Квадратну матрицю, визначник якої дорівнює нулю, називають виродженою матрицею. Квадратну матрицю, визначник якої не дорівнює нулю, називають невиродженою матрицею. |
Наприклад, визначник матриці 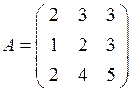 відрізняється від нуля (
відрізняється від нуля ( 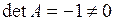 ), тому матриця
), тому матриця  не є виродженою.
не є виродженою.
| Теорема 1.2. | Для того, щоб матриця 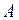 мала обернену мала обернену  необхідно і достатньо, щоб визначник матриці необхідно і достатньо, щоб визначник матриці 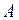 відрізнявся від нуля. відрізнявся від нуля.
|
Отже, невироджена матриця має обернену.
Обернену матрицю можна знайти за наступним правилом.
| Теорема 1.3. | Обернена матриця дорівнює транспонованій матриці алгебраїчних доповнень до елементів матриці  , яку поділено на визначник матриці , яку поділено на визначник матриці  . .
|
Для матриць другого і третього порядку згідно теоремі 1.3 будемо мати наступні формули для знаходження оберненої матриці:
 , (1.6)
, (1.6)
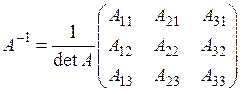 . (1.7)
. (1.7)
Правильність обчислення оберненої матриці перевіряють за допомогою співвідношень (1.1): 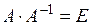 і
і 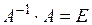 .
.
Алгоритм обчислення оберненої матриці
| 1) | Перевірка матриці  на невиродженість. на невиродженість.
|
| 2) | Знаходження алгебраїчних доповнень 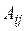 до всіх елементів до всіх елементів 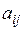 матриці матриці  . .
|
| 3) | Формування транспонованої матриці алгебраїчних доповнень. |
| 4) | Обчислення оберненої матриці. |
| 5) | Перевірка правильності обчислення оберненої матриці. |
|
|
|
Властивості обертання невироджених матриць
| 1) |  ; ;
|
| 2) |  ; ;
|
| 3) | 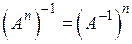 ; ;
|
| 4) | 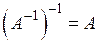 ; ;
|
| 5) | 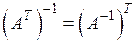 . .
|
| Приклад 1.4. | Знайти обернену до матриці 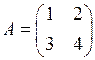 . .
|
Розв’язання. Визначник матриці 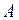 відрізняється від нуля:
відрізняється від нуля:
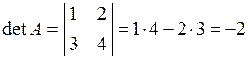 .
.
Отже матриця  є невиродженою і обернена до неї
є невиродженою і обернена до неї 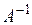 існує. Знайдемо алгебраїчні доповнення до кожного елементу вихідної матриці:
існує. Знайдемо алгебраїчні доповнення до кожного елементу вихідної матриці:
 ,
, 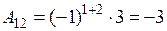 ,
, 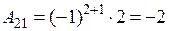 ,
, 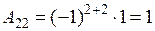 .
.
За формулою (1.6) можемо записати: 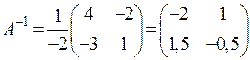 .
.
Перевірка підтверджує правильність проведених обчислень:
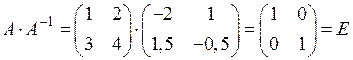 ,
, 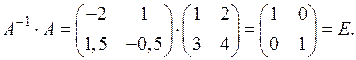
| Приклад 1.5. | Знайти обернену до матриці  . .
|
Розв’язання. Вихідна матриця  є не виродженою, оскільки
є не виродженою, оскільки 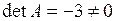 . Обчислимо алгебраїчні доповнення:
. Обчислимо алгебраїчні доповнення:

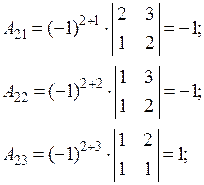
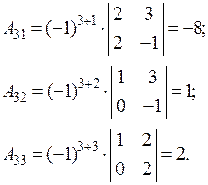
За формулою (1.7) маємо:
 , отже
, отже 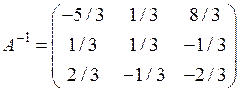 .
.
Рангом матриці 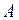 розмірності розмірності 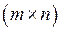 називають найбільший порядок відмінного від нуля мінору матриці і позначають називають найбільший порядок відмінного від нуля мінору матриці і позначають 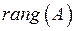 . Ненульовий мінор матриці, що визначає її ранг, називають базисним. . Ненульовий мінор матриці, що визначає її ранг, називають базисним.
|
Ранг матриці визначається порядком ненульового мінору, а не його значенням. Якщо 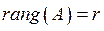 , то це означає, що існує хоча б один відмінний від нуля мінор порядку
, то це означає, що існує хоча б один відмінний від нуля мінор порядку 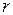 , а всі мінори порядку, більшого від
, а всі мінори порядку, більшого від  дорівнюють нулю. Зрозуміло, що
дорівнюють нулю. Зрозуміло, що  .
.
|
|
|
Системи лінійних рівнянь
Системою лінійних алгебраїчних рівнянь називають сукупність 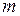 лінійних рівнянь відносно лінійних рівнянь відносно 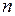 невідомих: невідомих:
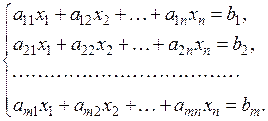 (1.8)
де (1.8)
де  - невідомі змінні, - невідомі змінні, 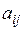 - коефіцієнти при невідомих, - коефіцієнти при невідомих, 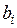 - вільні члени - вільні члени 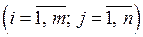 . .
|
Якщо всі вільні члени дорівнюють нулю 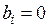 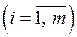 , то систему лінійних рівнянь (1.8) називають однорідною. У протилежному випадку, тобто коли не всі вільні члени нульові, систему (1.8) називають неоднорідною. , то систему лінійних рівнянь (1.8) називають однорідною. У протилежному випадку, тобто коли не всі вільні члени нульові, систему (1.8) називають неоднорідною.
|
Випишемо основну матрицю системи: 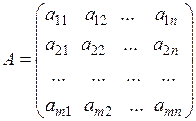 , яка складається з коефіцієнтів при невідомих; матрицю-стовпець вільних членів:
, яка складається з коефіцієнтів при невідомих; матрицю-стовпець вільних членів: 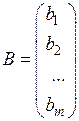 ; матрицю-стовпець невідомих:
; матрицю-стовпець невідомих: 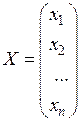 .
.
Використовуючи дії над матрицями, систему рівнянь (1.8) можна записати у матричній формі
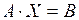 . (1.9)
. (1.9)
Розв’язком системи лінійних рівнянь (1.8) називають таку сукупність чисел 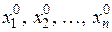 , яка перетворює всі рівняння (1.8) в числові тотожності. , яка перетворює всі рівняння (1.8) в числові тотожності.
|
Загальний розв’язок системи передбачає вираз основних невідомих через вільні. Частинний розв’язок одержують із загального наданням вільним змінним певних значень
Розширена матриця 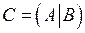 системи (1.8) або (1.9) складається з матриці
системи (1.8) або (1.9) складається з матриці 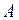 і стовпця вільних членів
і стовпця вільних членів  і має вигляд (для зручності стовпець вільних членів у розширеній матриці відділяють вертикальною лінією):
і має вигляд (для зручності стовпець вільних членів у розширеній матриці відділяють вертикальною лінією):
|
|
|
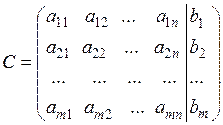 .
.
| Систему рівнянь називають сумісною, якщо вона має хоча б один розв’язок, і несумісною, якщо вона не має жодного розв’язку. |
| Систему називають визначеною, якщо вона має тільки один розв’язок, і невизначеною, якщо система має більше одного розв’язку. |
Однорідна система завжди є сумісною, оскільки завжди має нульовий розв’язок.
Дата добавления: 2019-02-13; просмотров: 279; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
