Властивості лінійних операцій над векторами
| 1) | 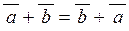 ; ;
|
| 2) | 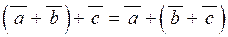 ; ;
|
| 3) | 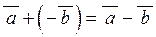 ; ;
|
| 4) | 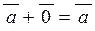 ; ;
|
| 5) | 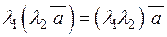 ; ;
|
| 6) | 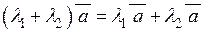 ; ;
|
| 7) | 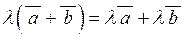 ; ;
|
| 8) |  ; ;
|
| 9) | 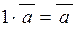 . .
|
Проекцією вектора 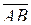 на вісь на вісь 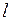 є вектор є вектор  , початком якого є точка , початком якого є точка 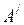 - проекція точки - проекція точки 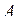 на вісь на вісь 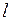 , а кінцем – точка , а кінцем – точка 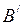 - проекція точки - проекція точки 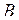 на вісь на вісь  .
Величиною проекції називають довжину вектору проекції .
Величиною проекції називають довжину вектору проекції 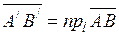 із знаком «+», якщо напрямок вектору із знаком «+», якщо напрямок вектору  співпадає з напрямком осі співпадає з напрямком осі  , і довжину , і довжину  із знаком «-» у протилежному випадку. із знаком «-» у протилежному випадку.
|
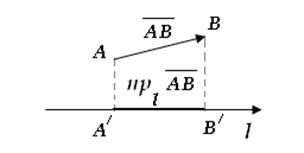
Рисунок 2.9 - Проекція вектора на вісь.
Основні властивості проекцій
| 1) | Проекції рівних векторів на вісь співпадають: якщо 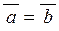 , то , то 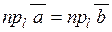 . .
|
| 2) | Проекція суми векторів на вісь дорівнює сумі проекцій доданків на цю вісь: 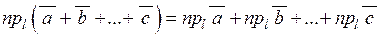 . .
|
| 3) | Проекція добутку вектора на число дорівнює добутку проекції цього вектора на число:  . .
|
| 4) | Величина проекції вектора на вісь дорівнює добутку модуля вектора на косинус кута 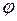 між вектором і віссю між вектором і віссю 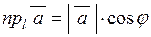 . .
|
| 5) | 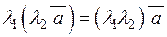 ; ;
|
| 6) | 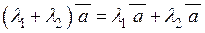 ; ;
|
| 7) | 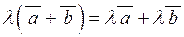 ; ;
|
| 8) | 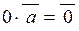 ; ;
|
| 9) | 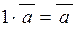 . .
|
Позначимо через 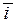 ,
, 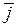 ,
, 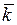 орти координатних осей (вектори одиничної довжини, що розташовані відповідно на осях
орти координатних осей (вектори одиничної довжини, що розташовані відповідно на осях 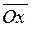 ,
, 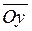 ,
, 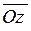 і напрямок яких співпадає з напрямком осей).
і напрямок яких співпадає з напрямком осей).
Координатамивектора 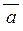 називають проекції цього вектора на координатні вісі. називають проекції цього вектора на координатні вісі.
|
Нехай 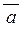 - вектор, що розглядається,
- вектор, що розглядається, 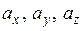 - проекції вектору
- проекції вектору 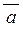 на координатні вісі:
на координатні вісі:
 ,
, 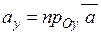 ,
, 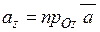 .
.
Тоді можна записати формулу розкладення вектору 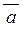 за координатними осями:
за координатними осями:
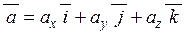 . (2.1)
. (2.1)
Після вибору в просторі декартової системи координат вектор 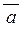 і трійка його координат
і трійка його координат 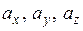 взаємно визначають один одне. Тому розкладення вектору зручно записувати у вигляді
взаємно визначають один одне. Тому розкладення вектору зручно записувати у вигляді 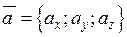 . Це запис вектора в координатній формі.
. Це запис вектора в координатній формі.
|
|
|
Якщо 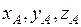 - координати точки
- координати точки 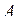 ,
, 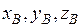 - координати точки
- координати точки 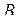 , то координати вектору
, то координати вектору 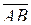 дорівнюють різницям відповідних координат його кінця
дорівнюють різницям відповідних координат його кінця  і початку
і початку 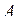 :
:
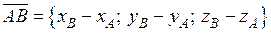 . (2.2)
. (2.2)
Дії над векторами в координатній формі
| 1) | Координати суми двох векторів дорівнюють сумам відповідних координат цих векторів: 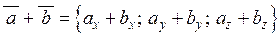 . .
|
| 2) | Координати різниці двох векторів дорівнюють різницям відповідних координат цих векторів: 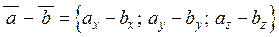 . .
|
| 3) | Координати вектору 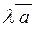 дорівнюють координатам вектору дорівнюють координатам вектору 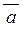 , які помножено на число , які помножено на число 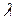 : : 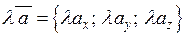 . .
|
Модуль вектора 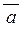 дорівнює кореню квадратному з суми квадратів його координат:
дорівнює кореню квадратному з суми квадратів його координат:
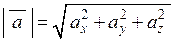 . (2.3)
. (2.3)
| Приклад 2.1. | У просторі задані точки 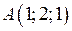 і і 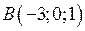 . Знайти величину проекції вектора . Знайти величину проекції вектора 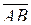 на вісь на вісь 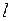 , якщо кут між ними складає , якщо кут між ними складає 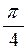 . .
|
Розв’язання. Спочатку знайдемо координати вектору  за формулою (2.2):
за формулою (2.2):  .
.
За формулою (2.3) обчислимо модуль вектору  :
:
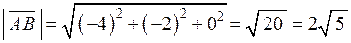 .
.
За четвертою властивістю проекції вектора на вісь знайдемо величину проекції: 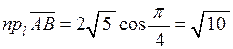 .
.
Скалярний добуток векторів
Скалярним добутком 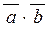 векторів векторів 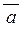 і і 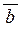 називають число, що дорівнює добутку їхніх довжин на косинус кута між ними: називають число, що дорівнює добутку їхніх довжин на косинус кута між ними:
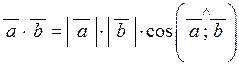 . (2.4) . (2.4)
|
Основні властивості скалярного добутку векторів
|
|
|
| 1) | 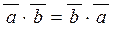 ; ;
|
| 2) | 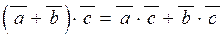 ; ;
|
| 3) | 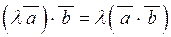 ; ;
|
| 4) | скалярний добуток двох ненульових векторів дорівнює нулю тоді і тільки тоді, коли ці вектори ортогональні:
 ; ;
|
| 5) | скалярний квадрат вектора дорівнює квадрату його довжини:
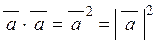 . .
|
Нехай вектори 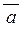 і
і 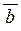 задані своїми координатами
задані своїми координатами 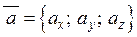 і
і 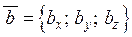 , тоді формула скалярного добутку векторів
, тоді формула скалярного добутку векторів 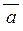 і
і 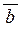 у координатній формі має вигляд:
у координатній формі має вигляд:
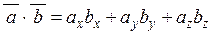 . (2.5)
. (2.5)
З відношення (2.5) випливає формула косинуса кута між векторами:
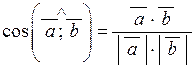 , (2.6)
, (2.6)
або у координатній формі з урахуванням відношень (2.3) і (2.5):
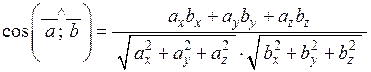 . (2.7)
. (2.7)
Проекція вектора 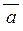 на вектор
на вектор  , тобто
, тобто 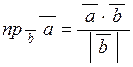 , у координатній формі має вигляд
, у координатній формі має вигляд
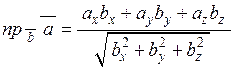 . (2.8)
. (2.8)
Оскільки орти декартової системи мають координати 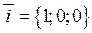 ,
, 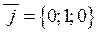 ,
, 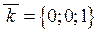 , то з формули (2.7) для будь-якого вектору
, то з формули (2.7) для будь-якого вектору 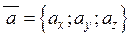 , одержимо наступні формули косинусів кутів з координатними осями або направляючі косинуси вектору
, одержимо наступні формули косинусів кутів з координатними осями або направляючі косинуси вектору 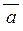 :
:
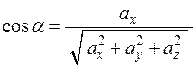 ,
,
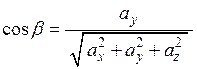 , (2.9)
, (2.9)
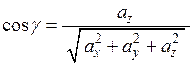 ,
,
де  - кути, що складаються вектором
- кути, що складаються вектором 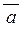 з осями
з осями 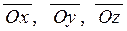 .
.
| Приклад 2.2. | Знайти 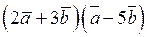 , якщо , якщо 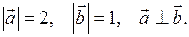
|
|
|
|
Розв’язання. 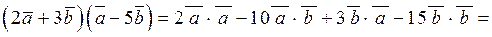
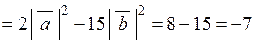 .
.
| Приклад 2.3. | Знайти кут між векторами 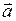 і і 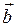 , якщо , якщо  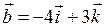 . .
|
Розв’язання. Маємо 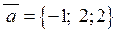 ,
, 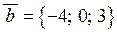 , звідки з урахуванням (2.3) і (2.5) знаходимо:
, звідки з урахуванням (2.3) і (2.5) знаходимо: 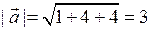 ,
, 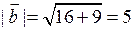 ,
, 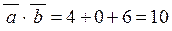 ,
, 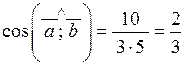 ,
, 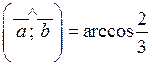 .
.
| Приклад 2.4. | Знайти кут між векторами 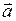 і і 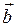 , якщо , якщо  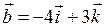 . .
|
Розв’язання. Маємо 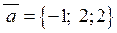 ,
, 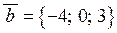 , звідки з урахуванням (2.3) і (2.5) знаходимо:
, звідки з урахуванням (2.3) і (2.5) знаходимо: 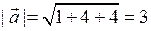 ,
, 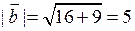 ,
, 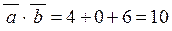 ,
, 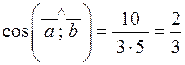 ,
, 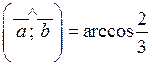 .
.
Векторний добуток векторів
Векторним добутком 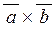 вектору вектору 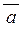 на вектор на вектор 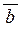 називають вектор називають вектор 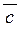 , що задовольняє умовам:
вектор , що задовольняє умовам:
вектор 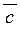 перпендикулярний кожному із векторів перпендикулярний кожному із векторів 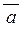 і і 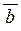 , отже, площині, в якій вони розташовані;
вектор , отже, площині, в якій вони розташовані;
вектор 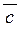 спрямований так, що, якщо дивитись з його кінця, то найкоротший поворот від першого вектора спрямований так, що, якщо дивитись з його кінця, то найкоротший поворот від першого вектора 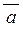 до другого вектора до другого вектора 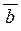 відбувається проти годинникової стрілки;
довжина вектора відбувається проти годинникової стрілки;
довжина вектора  чисельно дорівнює площі паралелограма, який побудовано, на векторах чисельно дорівнює площі паралелограма, який побудовано, на векторах 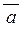 і і 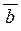 , як на сторонах: , як на сторонах:
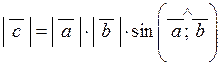 . (2.10) . (2.10)
|
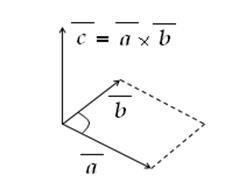
Рисунок 2.10 - Векторний добуток векторів.
Векторний добуток в координатній формі:
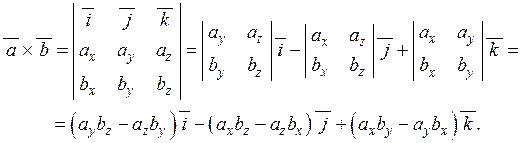 (2.11)
(2.11)
Дата добавления: 2019-02-13; просмотров: 236; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
