Напряжения и деформации. Закон Гука

Основные понятия. Метод сечений.

Растяжение или сжатие возникает, когда равнодействующие внешних нагрузок действуют вдоль оси стержня. В поперечном сечении стержня имеет место только одна внутренняя сила N, действующая вдоль его оси. Эту внутреннюю силу называют продольной силой или нормальной силой (действует по нормали к поперечному сечению). На рис. 2.1 изображен прямой стержень, работающий на растяжение.

Рис 2.1. Прямой стержень, работающий на растяжение

Правило знаков для продольной силы. Продольная сила будет положительной, если она вызывает растяжение, т.е., направлена от сечения.

Знак продольной силы не зависит от направления оси координат, а определяется физическим воздействием на сечение. Если продольная сила будет направлена к сечению, то она вызывает сжатие (сжимающая сила) и перед ней ставят знак «минус». Если она направлена от сечения, то перед ней ставят знак «плюс» (растягивающая сила). На рис. 2.2. изображена положительная продольная сила, действующая на крайние сечения малого элемента, вырезанного из прямого стержня.

Рис 2.2. К правилу знака продольной силы N

Знак сжимающей силы имеет значение в расчетах на прочность в строительстве. Бетон, кирпичная или каменная кладка плохо работают на растяжение и хорошо – на сжатие. Например, арки древних каменных храмов, сохранившиеся до сегодняшних дней – это элементы строительных конструкций, в поперечных сечениях которых имеют место только сжимающие продольные силы. Конечно, древние строители не выполняли расчетов, а набирали опыт по мере работы.

Сталь одинаково хорошо сопротивляется и сжатию, и растяжению. Стальную арматуру закладывают в растянутые зоны бетона для того, чтобы он не разрушался от растяжения. Получившийся материал называется железобетоном.

Метод сечений. Для определения внутренних усилий в стержнях используется метод сечений, суть которого состоит в следующем.

1. Разрезают стержень на две части плоскостью, перпендикулярной оси (проводят поперечное сечение).

2. Отбрасывают одну из двух частей стержня.

3. Заменяют действие отброшенной части на оставшуюся часть стержня неизвестными внутренними усилиями.

4. Уравнения равновесия, составленные для оставшейся части стержня, позволяют определить внутренние усилия.

Вычислив продольные силы в различных сечениях, можно построить график зависимости , который называется эпюрой продольной силы.

Дифференциальная зависимость между q и N

Рис 2.3. К выводу дифференциальной зависимости между q и N

Составим уравнение равновесия для малого элемента, вырезанного из стержня, загруженного распределенной нагрузкой q (рис. 2.3).

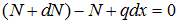
Отсюда получаем дифференциальную зависимость между q и N:

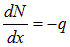
(2.1)

Первая производная от продольной силы по переменной х равна с обратным знаком интенсивности продольной нагрузки. Исходя из свойств производной, из (2.1) можно сделать вывод о том, что, если q(x) является полиномом n степени, то N(x)будет представлять собой полином n+1степени. Это позволяет определить, какой вид будет иметь график функции N(x)в зависимости от q(х). В дальнейшем нам пригодятся для изучения курса три следствия:

1) если q = 0 (т. е. нагрузка q отсутствует), то N(x) = const;

2) если q(x) = const, то есть является равномерно распределенной нагрузкой, то N(x) – линейная функция;

3) если q(x) = линейная функция, то N(x) – квадратная парабола.

Эпюра продольных сил

Эпюрой продольных сил называется график функции N(x).

Рассмотрим прямой стержень, загруженный продольными нагрузками и находящийся в равновесии (рис. 2.4). Предположим, что ось Ох (на рисунке не показана), направлена вправо.

Рис 2.4. Определение продольной силы методом сечений

Определим продольную силу в произвольном сечении К.

В соответствии с методом сечений отбросим левую часть и составим уравнение равновесия для правой части, направив неизвестную силу N от сечения (предполагая ее растягивающей):

Находим продольную силу:

(2.2)

Таким образом, продольную силу в поперечном сечении можно найти суммированием внешних сил, которые находятся справа от сечения.

Отбросим теперь правую часть и рассмотрим уравнение равновесия для левой части:

Находим продольную силу:

(2.3)

Отсюда следует, что продольную силу в поперечном сечении можно найти также суммированием внешних сил, которые находятся слева от сечения.

На основании формул (2.2) и (2.3) можно сделать следующий вывод: продольная сила в поперечном сечении стержня – это сумма проекций на ось стержня внешних сил, расположенных по одну сторону от сечения.

(2.4)

Продольной силой можно считать проекцию главного вектора системы внешних сил, расположенных с одной стороны от сечения, на ось стержня. Эта проекция приложена в точке центра тяжести сечения, причем, если она направлена в сторону внешней нормали по отношению к оставшейся части, то она будет положительной.

Проиллюстрируем, как можно найти силу N в произвольном сечении (рис. 2.5).

Рис 2.5. К определению продольной силы

Нужно провести сечение, перенести к нему силы, расположенные с одной стороны от сечения, и просуммировать их, причем те силы, которые «давят» на сечение, нужно брать со знаком «минус», а те силы, которые направлены от сечения, следует брать со знаком «плюс».

Отметим некоторые общие правила построения эпюр продольных сил.

Эпюра строится на линии, параллельной оси стержня (иногда ее называют базовой линией или базой эпюры). Через характерные сечения проводятся выносные линии, на которых в определенном масштабе откладываются значения N в этих сечениях и соединяются линиями. Над эпюрой указывается обозначение функции (в данных примерах N) и ее размерность. Эпюра заштриховывается перпендикулярно оси, при этом каждая штриховая линия как бы указывает значение N в соответствующем сечении. Внутри эпюры в кружочках указывается знак N на соответствующем участке. При этом, как правило, положительные значения откладываются в правую сторону (если эпюра построена на горизонтальной линии, то положительные значения откладывают вверх).

На основании изучения построенных эпюр и следствий из дифференциальной зависимости можно отметить характерные особенности эпюры N, которые обычно используют для ее контроля.

1. В сечении, где приложена сосредоточенная сила, на эпюре N имеется скачок на величину этой силы.

2. На участке, где приложена равномерно распределенная нагрузка, эпюра N имеет линейный характер, причем изменение функции N(х) на участке равно ql.

3. На участке, где отсутствует распределенная нагрузка, эпюра N является постоянной.

Напряжения и деформации. Закон Гука

Нормальные напряжения в поперечных сечениях. При центральном растяжении (сжатии) стержней в их поперечных сечениях действует только одно внутреннее усилие – продольная сила N.

Поэтому в этих сечениях будут возникать только нормальные напряжения . Поскольку других нормальных напряжений в поперечных сечениях нет, будем в дальнейшем опускать индекс у напряжения, обозначая .

В соответствии с гипотезой плоских сечений сечения, плоские и перпендикулярные оси стержня до деформации, остаются плоскими и перпендикулярными оси после деформации.

Можно показать, что применение этой гипотезы приводит к простой формуле для определения нормальных напряжений при растяжении и сжатии.

(2.5)

Эти напряжения постоянны по сечению (рис. 2.5)

Рис 2.5. Распределение нормальных напряжений по сечению при растяжении

При известной эпюре продольных сил формула (2.5) позволяет довольно просто построить эпюру . Для этого необходимо в характерных сечениях разделить значение силы N на площадь поперечного сечения А. Если площадь постоянна по длине стержня, эпюра будет полностью подобна эпюре N.

Напряжения на наклонных площадках. Рассмотрим элемент стержня, образованный поперечным и наклонным к оси стержня сечениями (рис. 2.7, а). Стержень растягивается силами F по его концам.

Рис 2.7. Напряжения на наклонных площадках

Обозначим площадь наклонного сечения А, тогда площадь горизонтальной площадки будет равна А ×соs α (рис. 2.7,б), где α – угол поворота нормали наклонного сечения относительно оси х. Очевидно, что продольная сила равна N = F = s_х × (А соs α) = p_n А и постоянна по длине стержня. Поэтому полные напряжения p_n = s_х соs α.

Разложим вектор полного напряжения p_n на две составляющие s_α и t_α и составим два уравнения равновесия и для выделенного треугольного элемента.

;

(2.6)

Обозначая s_x = s, из этих уравнений найдем

;

(2.7)

Из равенств (2.7) видно, что s_a и t_a являются периодическими функциями, зависящими от угла a наклона сечения. При различных углах a:

а) a = 0 (поперечное сечение); s_a = s; t_a = 0;

б) a = 90° (продольное сечение); s_a = 0; t_a = 0;

в) a = 45° (наклонное под углом 45° сечение); s_a = s /2; t_a = s/2.

Из второго равенства (2.7) можно установить, что касательные напряжения достигают максимума на площадках, наклоненных к поперечному сечению под углом 45 ° ( sin 90° = 1) и равны половине значения нормальных напряжений в поперечном сечении:

(2.8)

Максимальные нормальные напряжения возникают в поперечных сечениях и определяются по формуле (2.5).

Деформации. Рассмотрим деформированное состояние стержней при растяжении и сжатии. При растяжении длина стержня увеличивается, а поперечные размеры уменьшаются, при сжатии – наоборот. Это легко наблюдать в опытах с резиновыми образцами, в которых деформации достаточно велики.

Рис 2.8. Деформирование стержня при растяжении

Рассмотрим, какие деформации возникают при растяжении стержня (рис. 2.8).

Величина Dl = l – l₀ называется абсолютным удлинением, или абсолютной линейной продольной деформацией стержня(здесь l₀ – первоначальная длина, а l – длина после деформации). Величины Dh = h – h₀ и Db= b – b₀ называются абсолютными линейными поперечными деформациями (здесь h₀ и b₀ – первоначальные поперечные размеры, h и b – поперечные размеры после деформации). Абсолютные деформации измеряются в единицах длины (метрах, сантиметрах, миллиметрах).

Если разделить величины абсолютных деформаций на первоначальные размеры, то получим величины, называемые относительными линейными деформациями. Согласно принятым ранее обозначениям осей координат (х – вдоль оси стержня, а y и z – в поперечном сечении), относительные продольные деформации будут обозначаться 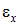, а относительные поперечные деформаци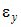и – и . Продольную и поперечные относительные деформации можно определить по формулам:

;

(2.9)

Учитывая, что , , 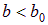можно заметить, что при растяжении стержня поперечные деформации будут отрицательными. Для изотропных материалов . Из многочисленных опытов установлено, что отношение поперечных деформаций к продольным для каждого конкретного материала является постоянной величиной:

(2.10)

Константа называется коэффициентом поперечной деформации, или коэффициентом Пуассона и является одной из двух упругих характеристик материала (постоянных упругости). Очевидно, что коэффициент Пуассона является безразмерной величиной. Значения для некоторых материалов приведены в табл. 2.1. Для всех материалов величина лежит в пределах от 0 до 0,5. Материал, у которого = 0,5, называетсянесжимаемым. Таким материалом, у которого = 0,5, является резина на основе натурального каучука. Материал, имеющий = 0, – это, например, кора пробкового дерева.

Учитывая, что продольные и поперечные деформации имеют разный знак, будет справедливым следующее выражение:

(2.11)

Обозначая e_x = e, e_y = e_z = e¢, формулу для определения коэффициента Пуассона можно переписать в часто встречающемся в учебниках по сопротивлению материалов виде:

(2.12)

Закон Гука. Связь между напряжениями и деформациями была установлена экспериментально в 1676 г. английским ученым Робертом Гуком Эта связь в случае одноосного растяжения (сжатия) имеет вид

(2.13)

и называется законом Гука. Для краткости можно опустить индексы и записать закон Гука в виде

или

(2.14)

Коэффициент пропорциональности Е, входящий в закон Гука, называется модулем упругости, или модулем Юнга. Модуль упругости является второй упругой характеристикой материалов после коэффициента Пуассона и характеризует важное их свойство – жесткость. Чем больше Е, тем более жесткий материал мы имеем.

Учитывая, что линейные деформации являются безразмерными величинами, можно заключить, что размерность модуля упругости такая же, как и у напряжений (МПа).

График зависимости s(e) представляет собой прямую линию, выходящую из начала координат (рис. 2.9). Графическая интерпретация модуля упругости на этом рисунке часто обозначается как тангенс угла наклона прямой к оси . Однако следует заметить, что запись tg следует воспринимать условно, так как размерность у модуля упругости – МПа, а тангенс – безразмерная величина.

Рис 2.9. Графическое изображение закона Гука

Значения модуля Юнга для разных материалов лежат в очень широких пределах. Например, для резины он равен 1–10 МПа, а для стали – больше 2·10⁵ МПа. В табл. 2.1 приведены примерные значения Е для некоторых материалов.

Таблица 2.1

Модули упругости Е и коэффициенты Пуассона ν

(примерные величины)

Материал	Е, МПа	ν
Сталь	» 2·10⁵	» 0,3
Алюминий, медь	» 1 ·10⁵	» 0,3
Бетон	» 2·10⁴	» 0,15
Кирпичная кладка	» 3·10³	» 0,2
Дерево	» 1·10⁴ вдоль волокон » 400 поперек волокон	» 0,45
Резина на основе каучука	»10	0,5
Пробковая кора	»5	0

Дата добавления: 2018-10-27; просмотров: 2571; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 Следующая ⇒

Мы поможем в написании ваших работ!