Структура и классификация супермногообразий
Когерентный пучок и категория аффинных схем
Структурная теория супермногообразий требует, чтобы сначала мы ввели ряд определений и свойств из алгебраической геометрии. А затем уже применили эти определения и свойства для суперслучая. Конечной целью, которую мы ставим перед собой в данной части, будет поиск алгебраических инвариантов для супермногообразий, которые позволят увидеть, насколько сильно структура супермногообразия отличается от классического случая. Сразу обратим внимание, что в этой части важно быть внимательным к типу категории, в которой производятся построения.
Следуя основополагающей работе Ж.-П.Серра, введем понятие когерентного пучка следующим образом. Пусть (X, Q(X)) – окольцованное пространство для топологического пространства X. Из определений, данных в первой части, мы знаем, что пучком Q(X)-модулей называется пучок ℱ на X, такой, что для каждого открытого множества U⊂X множество ℱ(U) является Q(X)|U-модулем и для каждого вложения открытых множеств V⊂U⊂X гомоморфизм ограничения согласован со структурой рассматриваемых модулей при помощи гомоморфизма соответствующих колец Q(X)|U⟶Q(X)|V.
Морфизмом пучков Q(X)-модулей будет называться такой морфизм пучков, что для каждого открытого множества U⊂X отображение ℱ’(U)→ℱ’’(U) является гомоморфизмом Q(X)|U-модулей, т.е. морфизмом, сохраняющим операции и отношения в кольце Q(X) при соответствующих отображениях.
|
|
|
Через s1,…,sp мы обозначим некоторый набор сечений пучка ℱ над открытым множеством U⊂X. Если теперь рассмотреть последовательность 𝑓1,…, 𝑓p элементов кольца Q(X)x в точке x, то рассматривая сумму вида
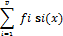
модуля ℱx мы можем видеть, что она порождает гомоморфизм пучков
𝑓 : Q(X)p = Q(X)⊕ …⊕Q(X) (p-экземпляров) ⟶ ℱ,
определяемый через соответствующие гомоморфизмы над открытыми множествами U⊂X.
Напомним, что если 𝑓: ℋ → ℒ – гомоморфизм пучков, то его ядро Ker𝑓={h∈ℋ, 𝑓(h)=0} является, очевидно, подпучком пучка ℋ, в то время, как образ Im𝑓 гомоморфизма двух пучков является лишь предпучком пучка ℒ. Для любой точной последовательности пучков 0→ ℋ’→ℋ→ℋ’’ и произвольного подмножества Y⊂X будет точна и индуцированная последовательность групп сечений 0→ℋ’(Y)→ℋ(Y)→ℋ’’(Y). Эпиморфизмом категории K называется морфизм m:A→B, такой, что из всякого равенства композиций морфизмов в категории K вида g∘m = h∘m следует равенство g = h. Эпиморфизм является категорным обобщением понятия сюръекции для функционального отображения 𝑓: X → Y при котором образ множества X этого отображения 𝑓 совпадает с множеством Y: 𝑓(X)=Y . Эпиморфизм и сюръективное отображения для многих категорий совпадают, но это не всегда так и, в частности, это не так для категории колец, где под морфизмами понимаются их вложения. Поэтому отметим, что отображение ℋ(Y)→ℋ’’(Y) не обязано быть эпиморфизмом в случае, если ℋ→ℋ’’ сюръективно. Однако для категории колец любой гомоморфизм кольца в одну из его локализаций является эпиморфизмом.
|
|
|
Двойственным к понятию эпиморфизма в теории категорий является понятие мономорфизма (часто обозначается, как A↪B). Мономорфизмом в категории K называется морфизм m:A→B, такой, что из всякого равенства композиций морфизмов в категории K вида m∘g = m∘h следует равенство g = h. Мономорфизмы представляют собой категорное обобщение понятия инъективной функции. Почти всегда эти определения совпадают, но в общем случае мономорфизм не соответствует инъективной функции. Например, в категории множеств мономорфизмы в точности соответствуют инъективным функциям, а вот в категории Div делимых (абелевых) групп с обычными гомоморфизмами групп существуют неинъективные мономорфизмы, например, отображение факторизации q: Q → Q/ℤ. Вот именно из-за таких нюансов, скрытых в определениях эпиморфизмов и мономорфизмов, которые возникают в случаях, для нас особенно важных, всегда следует обращать внимание на то, в какой категории происходят наши построения. Любопытно, что Бурбаки в своей аксиоматике использовали понятие мономорфизма просто как сокращённое обозначение инъективной функции, а С.Маклейн в книге по теории категорий подошел к понятию мономорфизма более обстоятельно. Он разделил морфизмы в конкретной категории, которым соответствует инъективная функция, и дополнительно ввел понятие “monic maps”, определяющее мономорфизмы в категорном смысле. И хотя такое разделение обычно не делается, мы для настоящей работы примем именно такой подход, как наиболее для нас удачный. Для интересующихся развитием этой темы можно порекомендовать трехтомник F.Borceux по теории алгебраических категорий, содержащий энциклопедический объем информации. Сделаем также следующее определение – если ℋ – подпучок пучка ℒ, то факторпучок ℒ/ℋ определим как пучок, порожденный предпучком U → ℒ(U)/ℋ(U).
|
|
|
Пучком соотношений назовем ядро K(s1,…,sp) = Ker 𝑓, где 𝑓: Q(X)p → ℱ. Пучок соотношений, как мы теперь знаем, является подпучком в пучке Q(X)p = ⊕(p)Q(X). Назовем пучок ℱ пучком конечного типа, если он порождается конечным числом своих сечений. Другими словами, пучок ℱ называется пучком конечного типа, если в окрестности U любой точки x∈U для каждой другой точки y из окрестности U любой элемент модуля ℱy является конечной линейной комбинацией сечений пучка ℱ в точке x с коэффициентами в кольце Q(X). Т.е. для пучка конечного типа ℱ и его сечений r1,…,rp над некоторой окрестностью точки x из X, порождающих модуль ℱx, эти же сечения порождают модуль ℱy.
|
|
|
Пучок модулей называется когерентным если он имеет конечный тип и для любых сечений s1,…,sp пучка ℱ над открытым множеством U⊂X пучок соотношений между этими сечениями является пучком конечного типа над U. Это определение носит локальный характер. Желая, чтобы определение выглядело глобально, иногда, за свойство когерентности принимают тот факт, что когерентный пучок локально изоморфен коядру Coker φ некоторого гомоморфизма φ: Q(X)q → Q(X)p. Но и это определение очевидно локально, поскольку требование к изоморфизму тоже лишь локально. С другой стороны, такое определение полнее раскрывает суть когерентности. Действительно, под коядром Coker φ|U отображения (в нашем случае локального над U) понимается факторпучок Q(U)p/Imφ|U и становится понятным, что все соотношения между sp+1,…,sq в пучке Q(X)q при q > p выводятся из рассмотрения и конечность Q(X)p влечет за собой конечность Q(X)q причем – для того же самого набора соотношений, если, конечно, не забывать, что мы имеем дело с гомоморфизмами пучков модулей, а не абстрактными пучками. Однако, при обобщении данной стратегии, нас ожидают трудности. Дело в том, что коядро для абстрактного гомоморфизма пучков может привести нас к пучку, у которого не выполняется свойство, при котором подпучок является пучком – свойство единственности сечений (см. определение пучка). Поэтому будем использовать в дальнейшем определение когерентности через соотношения между сечениями.
По отношению к отображениям когерентные пучки обладают очень хорошими свойствами. Так, ядро, коядро и образ любого гомоморфизма двух когерентных пучков являются когерентными пучками. Соответственно, если в короткой точной последовательности
0 ⟶ ℱ’ ⟶ ℱ ⟶ ℱ’’ ⟶ 0
два из трех пучков когерентны, то и третий когерентен тоже. Операции ℱ⊗ℱ’ и Hom(ℱ, ℱ’) над Q(X) с двумя когерентными пучками ℱ и ℱ’ дают снова когерентный пучок. Причем если для Hom(ℱ, ℱ’) все очевидно, то для тензорного произведения пучков ℱ⊗ℱ’ мы можем увидеть, как свойство когерентности распространяется на тензорное произведение, только рассмотрев более подробно, как вообще вводится тензорное произведение для пучков над пучком Q(X). Пусть Q(X) – пучок колец над X и 𝓡 – правый Q-модуль, а 𝓛 – левый Q-модуль. Обозначим через𝓡⊗Q𝓛 (именно в таком порядке) пучок абелевых групп, порождённый предпучком
U ⟶ (U) ⊗Q(U) 𝓛(U), U⊂X,
для которого операторы ограничения определяются естественным образом с помощью операторов ограничения пучков Q, 𝓡 и 𝓛. Если Q – пучок коммутативных колец, то тензорное произведение 𝓡⊗Q𝓛 также является Q-модулем. Слоем над точкой x является
(𝓡⊗Q𝓛)(x) = 𝓡(x) ⊗Q(x) 𝓛 (x)
а топология накрывающего пространства 𝓡⊗𝓛 характеризуется тем, что если r и s – сечения пучков 𝓡 и 𝓛 над открытым множеством U⊂X, то формула x→r(x)⊗s(x) определяет сечение тензорного произведения над U. Практически все алгебраические свойства тензорного произведения могут быть распространены на случай пучков. Поскольку когерентные пучки определяются своим пучком соотношений, теперь уже очевидно, что и тензорное произведение когерентных пучков также является когерентным пучком. В частности, для всякого левого Q-модуля, где Q – пучок колец с единицей, имеет место канонический изоморфизм Q⊗Q𝓛 = 𝓛.
Приведем интересный пример для тензорного произведения пучков, предложенный в свое время еще Ж. де Рамом в его классической книге по теории дифференцируемых многообразий. Пусть X дифференцируемое многообразие и E – расслоенное многообразие над X, слой которого является векторным пространством. Обозначим через Ω0 – пучок ростков дифференцируемых функция над X и через Ω0E – пучок ростков дифференцируемых сечений расслоения E, который является Ω0-модулем. Тогда сечения пучка
ΩpE = Ω0E ⊗Ω0 Ωp
представляют собой дифференциальные формы p-степени на X со значениями в E. Точно также, если обозначить через 𝒟’p пучок ростков потоков степени p на X, то потоки степени p со значениями E в суть сечения пучка
ΩpE = Ω0E ⊗Ω0 𝒟’p.
Когда p=0 мы получаем так называемые сечения-распределения расслоенного многообразия E. Развивая этот подход можно определить сечения-меры расслоения и т.д.
Для классического определения понятия схемы мы по возможности откажемся от работы с максимальными идеалами, а вместо них будем работать с простыми идеалами некоторого коммутативного кольца А с единицей. Это объясняется тем, что прообраз максимального идеала не всегда максимальный. Достаточно рассмотреть вложение кольца А без делителей нуля в поле 𝕂, если кольцо А не является полем, то прообраз нулевого идеала, максимального в 𝕂, не максимален в А. И начнем мы с определений, которые не используют свойство коммутативности. Кольцо R называется первичным, если произведение I·J≠∅ для любых его ненулевых двусторонних идеалов I и J. Первичность кольца R равносильна равенству нулю его аннуляторов и если a,b∈R ненулевые элементы кольца R, то, в случае первичности R, произведение a·R·b тоже ненулевое. Двусторонний идеал I кольца R называется вполне простым, если для любых двух элементов кольца a,b∈R из принадлежности произведения a·b∈I следует, что либо a∈I, либо b∈I. Это справедливо, когда в факторкольце R∕I нет делителей нуля. Переход от максимальных к простым идеалам предложил А.Гротендик в своих работах по алгебраической геометрии.
Для коммутативного кольца понятие первичного и вполне простого идеала совпадают, а соответствующий идеал называется простым. В коммутативном кольце A любой нильпотентный элемент принадлежит пересечению всех простых идеалов этого кольца. Множество всех собственных простых идеалов кольца мы будем называть спектром кольца и обозначать SpecA. Поскольку для простого идеала прообраз при любом гомоморфизме прост, то мы для любого гомоморфизма простых идеалов для двух колец φ: А → В, через сопоставление прообраза при обратном отображении колец, можем определить отображение φ*: SpecВ → SpecА, ассоциированное с φ. Простые идеалы из SpecA называются точками (конечно – в алгебраическом смысле).
Теперь рассмотрим мультипликативное, т.е. замкнутое относительно операции умножения и содержащее единицу, множество S⊂A. Множество S также называется мультипликативной системой. Построим кольцо частных AS (иногда встречается обозначение S-1A). Кольцо частных состоит из пар (a,s), s∈S, a∈A с отношением эквивалентности (a,s)∼(a',s'), называемым также условием эквивалентности Óре, по имени норвежского математика Ойстина Óре, выдающегося специалиста в области алгебры и теории графов. Данное соотношение эквивалентности задается следующим образом – пара (a,s) эквивалентна паре (a',s'), если существует элемент s''∈S, такой, что s''·(as'−a's)=0. Операции сложения и умножения в кольце частных AS определяются следующими правилами
(a, s) + (a', s') = (as'+sa', s·s'), (a, s)·(a', s') = (a·a', s·s').
Другими словами кольцо частных AS суть формальные дроби вида a/s и две такие дроби эквивалентны (представляют один и тот же элемент кольца частных) если выполнено условие Оре, и которое, в свою очередь, порождает в кольце А соответствующий идеал. Операции сложения и умножения в кольце частных AS можно записать более привычным образом в виде
a/s + a'/s' = (as'+ a's)/s·s', a/s · a'/s' = a·a'/s·s'.
С данными операциями кольцо частных AS приобретает структуру коммутативного кольца с единицей. Нулем в AS служит дробь вида 0/1, а единицей служит дробь вида 1/1. Построение кольца частных AS называется локализацией кольца А по множеству S. Если S – дополнение простого идеала в кольце А, то построение кольца частных по данному дополнению называется локализацией кольца по простому идеалу, такое же построение уместно если S – множество всех степеней некоторого элемента кольца. Именно процедура локализации является отправной точкой для всех построений в алгебраической теории схем. Это оправдано уже хотя бы тем, что локализация применима для произвольных А-модулей и она полностью повторяет построение для колец, в результате чего мы можем получить модуль частных.
В случае если кольцо А является целостным кольцом, т.е. кольцом без делителей нуля или, что то же самое, у которого нулевой идеал {0} является простым, то множество всех ненулевых элементов образует мультипликативную систему S. Кольцо частных по этой мультипликативной системе называется полем частных. Элементы поля частных имеют вид a/b где а и b элементы кольца А и знаменатель не нулевой b≠0. В поле частных действуют обычные арифметические правила для дробей, причем это наименьшее поле, в которое можно вложить А. Можно сказать, что введение кольца частных – это универсальный способ сделать некоторое подмножество кольца обратимым, а вводя поле частных, мы этим самым делаем все элементы кольца обратимыми в данном поле.
Приведем простые примеры. Поле рациональных чисел является полем частных для кольца целых чисел. Поле рациональных функций над некоторым полем будет полем частных для кольца многочленов над этим же полем. Четные числа образуют в кольце целых чисел простой идеал – локализацией кольца целых чисел для данного идеала будет кольцо дробей, у которых в несократимом виде знаменатель будет нечетным числом. Эти примеры показывают, какие очевидные соображения заложены в основу такой, на первый взгляд энигматичной теории, как алгебраическая теория схем.
Понятие кольца и поля частных понадобится нам немного позже, а пока сделаем одно важное замечание. Процедура локализации в алгебраической геометрии содержит в своей основе тот замечательный факт, что локальным инвариантом точки x многообразия X является локальное кольцо для данной точки. Под локальным кольцом мы имеем в виду кольцо, которое описывает локальные поведение функций на алгебраическом или обычном многообразии – это надо всегда помнить, чтобы избежать путаницы, связанной с прилагательным “локальное” в смысле рассмотрения свойств кольца для некоторого подмножества и локальности, как свойства, которое выполняется для всех простых идеалов. Это (локальное) кольцо состоит из всех функций, каждая из которых регулярная в какой-либо окрестности точки х. Однако, так как разные функции регулярны в разных окрестностях, то данная ситуация требует некоторой особой внимательности. Вообще, функция F: X→𝕂 на алгебраическом подмножестве X⊂𝔸n для некоторого поля 𝕂 (будем считать его алгебраически замкнутым) называется регулярной если найдется многочлен 𝑓∈𝕂[x1,…,xn] такой, что F = 𝑓|X . Отображение алгебраических подмножеств X→Y, где X∈𝔸n, Y∈𝔸m называется регулярным, если оно имеет вид 𝜙(x) = (𝜙1(x),…, 𝜙m(x)), где 𝜙i – регулярные функции на алгебраическом подмножестве X.
Например, регулярные функции на 𝔸1∖{a1,…,an} – это функции вида 𝑓(x)/g(x), где 𝑓,g∈𝕂[x] и все корни g лежат в множестве {a1,…,an}. Еще один пример: пусть X – плоская кривая x2+y2–1=0. Любое регулярное отображение X→𝔸2 задается парой многочленов: (x,y) ↦ (𝑓(x,y), g(x,y)). При этом разные пары многочленов могут задавать одно и то же отображение. Так отображения (x3, (x + y)2), (x – xy2, 2xy + 1) и (x5 + x3y2, 2x2 + 2xy + 2y2 – 2) совпадают на X.
Алгебраические подмножества или их открытые подмножества будем называть изоморфными, если между ними существуют взаимно обратные регулярные отображения. Приведем примеры изоморфных алгебраических подмножеств. Так функции перехода меду разными координатами на картах проективного пространства
𝜙j ∘ 𝜙i-1: 𝜙i (Ui⋂Uj) → 𝜙j (Ui⋂Uj)
являются регулярными изоморфизмами между открытыми подмножествами в 𝔸n. Поэтому, можно считать, что проективное пространство склеено из аффинных многообразий.
Проколотая прямая 𝔸1∖{0} и кривая {xy – 1}⊂𝔸2 также являются регулярно изоморфными. Взаимно обратные регулярные отображения задаются формулами 𝜙(x)=(x,1/x) и φ(x,y)=x.
Регулярно изоморфны и прямая 𝔸1 с параболой {y – x2= 0}⊂𝔸2. В этом случае регулярные отображения задаются формулами вида 𝜙(x)=(x,x2) и φ(x,y)=x. Аналогично этому примеру, график любого многочлена 𝑓(x) – это плоская кривая, изоморфная аффинной прямой.
Вернемся к нашим построениям. Если многообразие X неприводимо (т.е. не является объединением никаких меньших многообразий), то QX является подкольцом поля 𝕂(X), состоящим из всех функций 𝑓(x)∈𝕂(X), регулярных в точке x. 𝕂(X) является полем частных для координатного кольца 𝕂[X], многочленов над полем 𝕂. В таком случае мы можем видеть, что кольцо QX состоит из отношений вида 𝑓/g, где 𝑓 и g∈𝕂[X] и g(x)≠0. Если J – простой идеал в кольце А, то выбрав в качестве мультипликативной системы S разность A–J, мы получаем в качестве кольца частных AS локальное кольцо идеала J. Аффинной схемой мы будем называть локально окольцованное пространство (SpecA=X, Q(X)), где слой Q(X)x в точке x∈SpecA – локальное кольцо соответствующего простого идеала, т.е. кольцо частных AS, где S=A–x. Будем считать, что категория аффинных схем является для нас модельной категорией. Если кольцо А – суперкоммутативное кольцо, то такую аффинную схему мы будем называть аффинной суперсхемой, а соответствующую модельную категорию будем называть модельной категорией аффинных суперсхем.
Поскольку мы рассматриваем отношения многочленов в виде дробей, уместно будет дать еще одно определение регулярной функции в следующем виде. Функция F:X→𝕂 на открытом подмножестве алгебраического подмножества U⊂X⊂𝔸n называется регулярной, если для любой точки x∈U найдется такая окрестность точки x∈V⊂U и найдутся такие многочлены 𝑓 и g ∈ 𝕂[x1,…,xn], что g не обращается в ноль на V и F|V = (𝑓/g)|V. Получается, что для алгебраического подмножества в 𝔸n у нас есть два определения регулярной функции, так как подмножество открыто в самом себе. Они не равносильны – чтобы это показать, достаточно рассмотреть функцию 1/(x2+1) на 𝔸1 для вещественного поля ℝ. Действительно, в этом отношении и в числителе и в знаменателе находятся многочлены, не обращающиеся в ноль ни на каком открытом подмножестве. Поэтому они удовлетворяют лишь второму определению и вот почему нам в дальнейшем понадобятся проективные многообразия. При этом, первое определение для регулярной функции применить уже не удается. Однако, из теории поля известно, что для алгебраически замкнутого поля любая функция, локально представимая в виде отношения многочленов, всегда может быть представлена глобально как некоторый многочлен. Это вытекает из теории Галуа для расширения полей и использует понятие минимального многочлена. Для тех, кто заинтересовался данным вопросом можно порекомендовать целый ряд замечательных книг и монографий, связанных с теорией Галуа, наиболее удачными из которых являются книги С.Ленга и М.Рида.
Суперсхемой назовем локально окольцованное пространство (M,Q(M)), у каждой точки которого имеется такая открытая окрестность U, что (U,Q(M)|U) изоморфно аффинной суперсхеме в категории локально окольцованных суперпространств.
В данном определении суперсхемы мы предполагаем, что пучок Q(M) для ℤ2–градуированного кольца A над выбранной открытой окрестностью имеет суперкоммутативную структуру, а классическая коммутативность является просто частным случаем. Современное определение суперсхемы см. в §.2.2.
Исходя из того, что точки, над которыми заданы кольца частных – это элементы спектра, а росток Q(X)x в точке x∈SpecA – локальное кольцо соответствующего простого идеала, т.е. кольцо частных AS, где мультипликативная система – это просто разность S=A–x, мы получаем достаточно удачный с математической точки зрения объект. Кажется, что схема устроена настолько алгебраически стройно и на первый взгляд просто, что не сразу видно какие могут содержаться особенности в её устройстве. Но мы столкнемся с особенностями алгебраического устройства схем уже довольно скоро.
Поскольку мы имеем дело с категорией аффинных схем, которая является модельной категорией для определения схемы – сделаем категорную формулировку для конструкции поля частных. Если рассматривать категорию целостных колец, в которой морфизмами являются инъективные гомоморфизмы колец, то существует забывающий функтор из категории полей в эту категорию. Существование такого функтора следует из леммы о композиции гомоморфизмов колец и следствия из неё.
Лемма (о композиции гомоморфизмов колец). Композиция гомоморфизмов является гомоморфизмом. Если 𝑓: M ⟶ M' – гомоморфизм колец (и вообще, гомоморфизм любых моноидов, т.е множеств с некоторой заданной ассоциативной бинарной операцией на данном множестве и существованием единицы для этой операции), а x∈M – обратимый элемент, то 𝑓(x)∈M' – обратим и 𝑓(x)-1 = 𝑓(x-1).
Доказательство. Обозначим через ∘ мультипликативную операцию на нашем кольце (для общего случая – бинарную на моноиде). Тогда 𝑓(g(x∘y)) = 𝑓(g(x)∘g(y)) = 𝑓(g(x))∘ 𝑓(g(y)), откуда следует первая часть леммы. Для доказательства второй части достаточно заметить, что 𝑓(x-1)∘ 𝑓(x) = 𝑓(x-1∘x) = 𝑓(e) = e', 𝑓(x)∘ 𝑓(x-1) = 𝑓(x∘x-1) = 𝑓(e) = e', то есть 𝑓(x-1) = 𝑓(x)-1. ∎
Следствие. Любой гомоморфизм из поля в кольцо является вложением.
Доказательство. Из леммы о композиции гомоморфизмов колец любой обратимый элемент поля, относительно его мультипликативной структуры, переходит в обратный элемент. Следовательно, всякий ненулевой элемент поля переходит в ненулевой элемент кольца. В частности, ядро гомоморфизма из поля в кольцо равно нулю и следовательно этот гомоморфизм является вложением. ∎
Итак, мы имеем забывающий функтор из категории полей в категорию целостных колец, поскольку гомоморфизмы полей в категорию целостных колец мономорфны. У этого функтора существует левый сопряженный функтор, который сопоставляет целостному кольцу его поле частных. Левым его делает соответствующая коммутативная диаграмма, которая рассматривается для мономорфизмов полей в категорию целостных колец.
Теперь, также как мы сделали в первой части для вполне примарных колец, выпишем наиболее полезные для нас сведения, касающиеся колец частных.
(I) Кольцо частных AS имеет каноническую структуру алгебры над кольцом А, поскольку существует канонический гомоморфизм 𝛹:A⟶AS, сопоставляющий каждому элементу a∈A дробь a/1, a↦a/1. Ядро этого гомоморфизма является идеалом IS=Ker𝛹;
(II) Если мультипликативная система S не содержит делителей нуля, то гомоморфизм 𝛹:A⟶AS инъективен и кольцо A вложено в свое кольцо частных AS по мультипликативной системе S, при этом дробь a/s является единственным решением уравнения sx=a, a∈A, s∈S;
(III) Если мультипликативная система S состоит только из одних обратимых элементов кольца A, то канонический гомоморфизм 𝛹:A⟶AS превращается в изоморфизм 𝛹:A≌AS, поскольку любая дробь a/s будет сократимой в кольце A;
(IV) Если два элемента a и s принадлежат мультипликативной системе S, тогда в кольце частных AS содержатся дроби a/s и s/a, и их произведение равно единице, поэтому они обратимы;
(V) Любой обратимый элемент кольца частных AS имеет вид ea/s, где a, s∈AS, и e – некоторый обратимый элемент кольца A;
(VI) Локализация кольца по простому идеалу P порождает в результате локальное кольцо AP, единственный простой идеал которого порожден образами элементов идеала P, процесс перехода от A к AP называется локализацией кольца относительно P и AP состоит из всех a/s, s∉P, а S=A∖P мультипликативно замкнутое подмножество.
Спектральная топология
Проводя алгебраизацию определения когерентного пучка, мы воспользовались тем общим и, без сомнения, важнейшим подходом в алгебраической геометрии, когда имея некоторые элементы 𝑓 из кольца A, мы рассматриваем их уже как функции на SpecA. В этом подходе, который отражает фундаментальную двойственность вида “пространство (многообразие) ⬌ функции на пространстве (многообразии)” и состоит суть алгебраического подхода. Мы видим эту двойственность и в том, как определяются окольцованные пространства, и в том, как вводится понятие аффинных схем, и в том, как устроена, например, алгебра теории Гельфанда (где преобразования Гельфанда являются основой алгебраической техники). И этот список применения фундаментальной двойственности для алгебраизации функционально заданных объектов можно продолжать далее, поскольку данный метод является общим местом современной математики. Так, например, для двух топологических пространств X и Y, и отображений 𝜑: X⟶Y, непрерывным функциям 𝑓, как классу морфизмов, заданному между этими двумя топологическими пространствами соответствует отображение 𝜑*:R(Y)⟶R(X) колец функций на этих пространствах, задаваемое формулой
𝜑*( 𝑓)(x) = 𝑓(𝜑(x)).
Мы уже видели, вводя понятие спектра, что если пространство X=SpecA, то рассматривая точку x, или, по определению, некоторый простой идеал Px, под символом 𝑓(x) понимается равенство 𝑓(x) = 𝑓 mod Px и, далее, предполагается, что 𝑓(x) принадлежит полю частных 𝕂(X) кольца A/Px. Таким образом, каждой точке x из SpecA приводится в соответствие поле частных 𝕂(X), которому принадлежит значение функции 𝑓 в точке x. Строя пучок колец (структурный пучок для окольцованного пространства, вводимый в первой части) мы могли видеть, что функции, которые обращаются в 0 для всех точек из SpecA, представлены нильпотентными элементами. Поэтому можно говорить о том, что пересечение всех простых идеалов Px в слое структурного пучка является нильрадикалом. В коммутативном случае нильрадикал – это идеал, состоящий из всех его нильпотентов. В некоммутативном случае нильрадикал можно ввести разными способами. Когда мы говорим о том, что нильрадикал понимается как пересечение всех простых идеалов, то имеем в виду, так называемый, нижний нильрадикал. Помимо нижнего нильрадикала можно ввести понятие верхнего нильрадикала – как идеала, порожденного всеми нильпотентными идеалами и нильрадикала Левицкого – как максимального локально нильпотентного идеала. Причем в случае нётеровости ростков пучка для некоторой окрестности выбранной точки, то есть исполнения условия обрыва возрастающих цепей идеалов (где всякая последовательность идеалов P1⊂P2⊂…⊂Pn⊂…, а для некоммутативных колец – левых идеалов, {\displaystyle p_{1}\subset p_{2}\subset \dots \subset p_{n}\subset \dots } стабилизируется, т.е. {\displaystyle p_{n}=p_{n+1}=\dots ,} Pn=Pn+1=…, начиная с некоторого n) все три определения нильрадикала совпадают. Для нашего случая важны два следующих факта. Во-первых, что пересечение всех максимальных идеалов (т.е. радикал Джекобсона) содержит нильрадикал. И, во-вторых, что факторкольцо по его нильрадикалу, который является пересечением всех его простых идеалов, не содержит нильпотентных элементов.
Примеры колец, не являющихся нётеровыми, как правило, гораздо сложнее нётеровых примеров. Так, примером ненётерового кольца является кольцо многочленов от бесконечного числа переменных ℚ[x1, x2, x3, …] , элементами которого, по определению, являются всевозможные конечные суммы взятых с рациональными коэффициентами мономов вида x 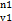 x
x 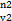 … x
… x  (произведение конечного числа переменных x
(произведение конечного числа переменных x  в некоторых степенях). Его идеал (x1, x2,…), состоящий из всех многочленов без свободного члена, нельзя породить конечным множеством многочленов. Более того, подкольцо нётерова кольца может не быть нётеровым. Например, кольцо формальных комплексных степенных рядов ℂ[z] нётерово, тогда как его подкольцо образованное рядами, сходящимися всюду в ℂ ненётерово.
в некоторых степенях). Его идеал (x1, x2,…), состоящий из всех многочленов без свободного члена, нельзя породить конечным множеством многочленов. Более того, подкольцо нётерова кольца может не быть нётеровым. Например, кольцо формальных комплексных степенных рядов ℂ[z] нётерово, тогда как его подкольцо образованное рядами, сходящимися всюду в ℂ ненётерово.
В пространстве SpecA можно ввести топологию. Для начала, поступим наиболее формальным образом. Будем требовать, чтобы множество нулей любой функции в такой топологии было замкнутым. Чтобы топология удовлетворяла данному условию, мы с каждым множеством E⊂A свяжем множество V(E)⊂SpecA, состоящее из всех простых идеалов Px для которых E⊂Px. Тогда мы немедленно получаем, что 𝑓(x)=0 при всех 𝑓∈E. Для множества V(E)⊂SpecA выполняются следующие очевидные соотношения:
V(⋃𝛼E𝛼) = ⋂𝛼V(E𝛼), V(J) = V(E')⋃V(E''),
где J – пересечение идеалов, порожденных подмножествами E' и E''. Топология, в которой все V(E) являются замкнутыми подмножествами, называется спектральной топологией или топологией Зарис c кого. Открытые множества D(𝑓) = SpecA–V(𝑓) называются главными открытыми множествами и образуют базис спектральной топологии. Пространство SpecA бикомпактно, т.е. из любого (не обязательно счётного, как в случае компактности) покрытия открытыми множествами можно выбрать конечное подпокрытие, но нехаусдорфово, поскольку в нем существуют незамкнутые точки. Можно даже утверждать, что особенностью топологии Зарисского является её нехаусдорфовость практически во всех нетривиальных построениях – мы коснемся этого вопроса немного позже.
Данное формальное определение топологии Зарисского нуждается в ряде комментариев. Топология на SpecA носит имя американского алгебраиста Оскара Зарисского и была введена им в золотое время развития алгебраических конструкций в середине XX века. Иногда эту топологию также связывают с именем М. Стоуна. Поскольку, когда было дано определение топологии для алгебраических многообразий, исследования аффинных и проективных многообразий шли гетерогенными путями, соответственно и определения топологии для них несколько различались. Но затем эти определения удалось объединить. Зачем нам понадобилось охватить в наших рассмотрениях не только аффинные, но также и проективные многообразия, будет понятно из дальнейшего, когда мы сделаем необходимые определения. Но уже здесь заметим, что структурная теория супермногообразий настолько комплексно впитала в себя разнообразные разделы алгебраической геометрии, что и проективные многообразия также потребуются для наших построений. По меньшей мере, делая различные варианты для регулярных функций, мы, неявно, уже подразумевали в рассмотрении и проективные многообразия.
Напомним, что аффинным n -мерным пространством 𝔸n над полем 𝕂 называется множество наборов (x1, …, xn), x i ∈ 𝕂 элементов поля 𝕂 длины n. Можно неформально понимать аффинное пространство как векторное пространство, в котором отсутствует начальная точка. Поэтому иногда требуется определение, где уточняется связь между точками и векторами. Кортеж (или, как ещё иногда говорят, “n-мерный вектор”) в математике – это упорядоченный набор из n элементов (n – любое натуральное число), называемое его компонентами, или координатами. Два кортежа равны в том и только том случае, когда они имеют одинаковую длину и их соответствующие координаты равны. Используя это понятие, аффинным пространством называют либо вырожденное пустое множество, либо кортеж 〈(A, V, (+))〉, состоящий из непустого множества точек A, векторного пространства V и действия (+):A⨯V→A, удовлетворяющего следующим свойствам:
1. ∀a ∈ A : a + 0 = a;
2. ∀v,w ∈ V, a ∈ A: (a + v) + w = a + (v + w);
3. Для всех a из A отображение (a+) биективно (сюръективно и инъективно одновременно, т.е. такое, когда каждому элементу одного множества соответствует ровно один элемент другого множества).
Из этих свойств, следует, что и для всех векторов v из V отображение (+v) тоже биективно. Размерность аффинного пространства 〈(A, V, (+))〉 равна размерности векторного пространства V. Как видим, в данном определении существенный для нас момент, а именно – основное поле 𝕂, не отображается явно, поэтому мы будем использовать первое определение аффинного пространства. Вводя топологию Зарисского на аффинном пространстве, мы тем самым превращаем его в аффинное многообразие. Замкнутым множествам в топологии Зарисского соответствуют так называемые алгебраические множества. В такой терминологии аффинное алгебраическое многообразие является, по определению, неприводимым алгебраическим множеством, т.е. множеством, которое не представимо в виде объединения двух меньших алгебраических множеств.
Мы также знаем, что переход от аффинной плоскости к проективной плоскости получается добавлением целой прямой, состоящей из бесконечно удаленных точек. Поэтому дадим такое определение проективного пространства.
Проективным n -мерным пространством ℙn над полем 𝕂 называется фактор множества ненулевых наборов (x0, …, xn)∈ 𝕂n+1 по отношению эквивалентности: (x0, …, xn) ∼ (t x0, …, t xn), t≠0. Класс такого набора обозначается (x0 : … : xn). В инвариантом виде определение проективизации ℙ(V) векторного пространства V размерности n+1 сводится к тому, что ℙ(V) – это множество прямых в векторном пространстве V, проходящих через 0.
В полном соответствии с аффинным случаем – проективное алгебраическое многообразие – это неприводимое замкнутое в топологии Зарисского подмножество проективного пространства.
Теперь подойдем к введению спектральной топологии развернуто. Как мы видим, топология Зарисского задается на фиксированном классе замкнутых множеств. Напомним, что для этого должны быть выполнены три свойства – всё пространство и пустое множество считаются замкнутыми, из замкнутости двух подмножеств следует, что их объединение замкнуто, и из замкнутости произвольного (не обязательно конечного) набора множеств следует, что их пересечение замкнуто. Напомним, что алгебраическим подмножеством аффинного пространства 𝔸n над полем 𝕂 называется множество решений некоторой (возможно, бесконечной) системы уравнений 𝑓𝛼(x1, …, xn) = 0, где 𝑓𝛼∈𝕂[x1, …, xn] – многочлены. Так точка (a1, … ,an) задается уравнениями xi–ai=0, а график y=sinx не является алгебраическим подмножеством. На самом деле давно известно, что всегда достаточно лишь конечного числа уравнений, а остальные будут из них следовать, так, например, теорема Гильберта о базисе (не путать с теоремой Гильберта о нулях!) утверждает, что кольцо многочленов над полем от нескольких переменных нётерово. Подробный разбор этих теорем мы сделаем немного позже.
И раз уж мы вспомнили о Давиде Гильберте, то уместно будет напомнить и то, что именно он содействовал устройству немецкого математика – Эмми Нётер в Геттингенский университет и добился этого, несмотря на предрассудки тех лет в отношении женщин, занимающихся математикой. Через некоторое время она смогла получить должность профессора в этом университете. Такие выдающиеся математики, как Жан Дьёдонне, Герман Вейль, Петр Сергеевич Александров и, конечно, сам Гильберт, считали, что Амалия Эмми Нётер является наиболее выдающейся женщиной в истории математики. Можно с уверенностью полагать, что это справедливо и по настоящее время, если учитывать её значительный вклад в развитие математики, особенно в разделы, связанные с теорией инвариантов и теорией идеалов коммутативных колец. Физикам Эмми Нётер хорошо известна благодаря своей концептуальной теореме, утверждающей, что каждой непрерывной симметрии для физической системы соответствует некоторый закон сохранения, например такой, как закон сохранения электрического заряда при калибровочной симметрии. Ученик Нётер – выдающийся алгебраист Эмиль Артин, работая с Нётер, рассматривал в применении к коммутативным кольцам цепочки убывающих идеалов. Соответствующие ассоциативные кольца с единицей, в которых выполнено условие обрыва убывающих цепей идеалов получили название – артиновы. Иногда встречаются утверждения, что нётеровость и артиновость кольца – это двойственные утверждение по отношению к условию обрыва соответствующих цепей, но это не совсем так. Существует теорема Хопкинса-Левицкого, показывающая, что условие артиновости кольца сильнее, чем двойственное ему условие нётеровости. Другими словами, любое артиново кольцо является нётеровым, а обратное утверждение неверно. Вообще, для алгебры, артиновы кольца интересны для работы именно в силу своего простого устройства – более просто утроены лишь только поля. Так, если А – некоторое локальное артиново кольцо, а 𝔐 – его максимальный идеал, то для такого кольца равносильно условие, что любой идеал в нем главный (т.е. порожден одним элементом) и условие, что его максимальный идеал 𝔐 главный. Более того, для таких колец dim𝕂(𝔐∕𝔐2)≤1, что делает их еще ближе по структуре к полям.
Нётеровость для алгебраического подмножества можно определять не через условия обрыва возрастающих цепей идеалов, а просто как свойство кольца, в котором любой идеал конечно порожден. Стабилизация таких цепочек после некоторого количества итераций не вызывает сомнений, хотя на первый взгляд и не совсем очевидна, поэтому докажем следующую лемму.
Лемма (об условиях нётеровости для коммутативного кольца). Для нётерова кольца R следующие свойства попарно эквивалентны:
(I) Любое подмножество M⊂R содержит конечный набор элементов a1, a2,…, ak∈M, порождающих тот же идеал, что и M;
(II) Любой идеал P⊂R конечно порожден;
(III) Любая бесконечно возрастающая цепочка вложенных идеалов P1⊂P2⊂…⊂Pn⊂…, {\displaystyle p_{1}\subset p_{2}\subset \dots \subset p_{n}\subset \dots } стабилизируется, в том смысле, что {\displaystyle p_{n}=p_{n+1}=\dots ,} Pn=Pn+1=…, начиная с некоторого n.
Доказательство. Ясно, что (I) ⇒ (II). Чтобы доказать (II) ⇒ (III), заметим, что объединение всех идеалов P=⋃Pn цепочки тоже является идеалом. Согласно (II), идеал P порожден конечным набором элементов. Все они принадлежат некоторому идеалу Pn, тогда Pn=P=Pn+1. Для доказательства (I) ⇒ (III) будем по индукции строить цепочку идеалов Pn=(a1, a2, …, ak), начав с произвольного элемента a1∈M и добавляя на k шагу очередную образующую ak∈M∖Pk-1 до тех пор, пока это возможно, т.е. до тех пор, пока M⊄Pk. Так как Pk-1⊈Pk, то этот процесс не может продолжаться бесконечно, и на некоторой итерации мы получим идеал, содержащий всё множество M, а значит и совпадающий с идеалом, порожденным множеством M. ∎
Соответственно, идеалом алгебраического подмножества можно считать множество всех многочленов, тождественно обращающихся в ноль на данном алгебраическом подмножестве. Неприводимое алгебраическое многообразие, по определению, не представимо в виде объедения меньших алгебраических подмножеств (пример – кольцо непрерывных функций), а если мы рассмотрим приводимые алгебраические подмножества, те самые, которые относятся к нетривиальному нётеровому случаю, то ситуация для них полностью описывается следующей теоремой:
Теорема (о цепочках вложенных алгебраических подмножеств). Любая строго убывающая цепочка вложенных алгебраических подмножеств в аффинном пространстве 𝔸n над полем 𝕂 конечна. Если некоторое неприводимое подмножество X⊂X1⋃…⋃Xm, тогда существует такое i, что X⊂Xi. Любое алгебраическое подмножество в 𝔸n раскладывается в конечное объединение попарно не вложенных неприводимых подмножеств, причем единственным образом (эти подмножества называются неприводимыми компонентами алгебраического подмножества).
Доказательство. Пусть 𝔸n⊃X1⊃X2⊃… – бесконечная цепочка строго убывающих алгебраических подмножеств. Тогда I(X1)⊂I(X2)⊂…⊂𝕂[x1,…,xn] – бесконечная цепочка строго возрастающих идеалов, что противоречит условию нётеровости кольца 𝕂[x1,…,xn], поскольку оно конечно порожденное. И, следовательно, любая строго убывающая цепочка вложенных алгебраических подмножеств в аффинном пространстве 𝔸n над полем 𝕂 конечна.
Далее, пусть X=(X⋂X1)⋃(X⋂(X2⋃…⋃Xm)). Так как X неприводимо, то X=(X⋂X1) или X=X⋂(X2⋃…⋃Xm), значит X⊂X1 или X⊂X2⋃…⋃Xm и по индукции существует такое i, что X⊂Xi.
Теперь докажем существование разложения. Пусть X приводимо, тогда можно записать его в виде объединения X=X'⋃X''. Если оба подмножества X' и X'' раскладываются в объединение неприводимых, то и подмножество X также раскладывается в объединение неприводимых подмножеств. Если это не так, то обозначим через X1 то из подмножеств X' и X'', которое не складывается в объединение неприводимых подмножеств и применим индукцию к этому процессу. Получим бесконечную убывающую последовательность вложенных замкнутых подмножеств, что противоречит тому, что такая последовательность должна быть конечна. Для завершения доказательства существования удалим все вложенные компоненты.
Теперь докажем единственность разложения. Пусть X=⋃Xi=⋃Xi'. Тогда, как уже показано, существует такое s, для которого X⊂Xs'. Аналогично, Xs' вложено в некоторое из подмножеств Xi. Из того, что все Xi попарно не вложены, получаем, что X1=Xs'. И таким же образом поступаем для всех остальных компонент. ∎ {\displaystyle n}) все три)
Для того, чтобы ввести на алгебраическом подмножестве V аффинного или проективного пространства топологию Зарисского через замкнутые подмножества, мы назовем замкнутыми подмножествами всевозможные алгебраические подмножества для V. Соответственно, открытыми подмножествами будут их дополнения до всего подмножества V. То, что это действительно топология, следует из теоремы о цепочках вложенных алгебраических подмножеств. Заметим, что теперь способ задания спектральной топологии, приспособленный для аффинных подмножеств и его версия для проективного пространства, становятся гораздо более похожими, чем при их задании через формальные определения.
В отношении проективных пространств можно сказать следующее. У алгебраического подмножества в проективном пространстве есть покрытие из открытых аффинных подмножеств, равно как и у любой точки алгебраического подмножества в проективном пространстве есть аффинная окрестность.
Для аффинного пространства 𝔸n над полем 𝕂 базис топологии Зарисского на алгебраическом подмножестве X⊂𝔸n образуют (главные открытые) множества X𝑓={x∈X, 𝑓(x)≠0}, 𝑓∈𝕂[x1,…,xn], которые мы в нашем формальном определении обозначили через D(𝑓). Это означает, что любое открытое множество U⊂X является объединением некоторого числа таких (главных) открытых множеств. И это действительно так, поскольку любое открытое подмножество U⊂X есть дополнение до множества нулей некоторого набора многочленов 𝑓𝛼, при этом U=⋃X𝑓𝛼.
Приведем примеры. Спектр поля 𝕂 – это топологическое пространство из одного элемента (общей точки), топологическое дополнение к которому является данным полем.
Замкнутые подмножества аффинной прямой – это конечные подмножества или вся прямая. Соответственно, открытые подмножества – это пустое множество или вся прямая, кроме конечного множества точек. Окрестность точки P∈𝔸1 – это множество, полученное удалением из 𝔸1 конечного числа точек, отличных от P.
Чтобы пример был еще более наглядным – рассмотрим кольцо целых чисел ℤ. Поскольку все целые числа представимы в виде произведения простых чисел, то точками спектра Specℤ будут точки, состоящие из простых чисел, которые соответствуют своим простым идеалам, связанным с данным простым числом, но это еще не весь спектр. У кольца есть еще один простой идеал, соответствующий нулю. Таким образом, в спектр войдет также некоторая общая точка, которая будет соответствовать данному идеалу, и дополнение для которой совпадает со всем пространством ℤ. Если перейти к замкнутым множествам для Specℤ , то они состоят из конечных подмножеств множества простых чисел, а также из всего спектра (т.е. из множества всех простых чисел). Любопытно, что Hom(ℤ, ℤ) состоит лишь из тождественного автоморфизма, в то время как у Specℤ автоморфизмы образуют группу перестановок бесконечного (счетного) числа элементов, ведь мы можем произвольно переставлять простые идеалы этого спектра, являющиеся его замкнутыми точками.
Но бывает и наоборот. Так, если А – кольцо с единственным простым идеалом, например поле 𝕂 или супералгебра Грассмана 𝝠(q) над этим полем, то геометрически SpecA это одна замкнутая точка, но автоморфизмы кольца А могут составлять очень богатую группу автоморфизмов (даже группу Ли). Это хорошо понятно физикам, которые трактуют такие одноточечные схемы, как подобные элементарным частицам, у которых имеются некоторые внутренние степени свободы. Но если кольцо А имеет нетривиальный спектр, то картина существенно усложняется.
Если мы имеем аффинное многообразие 𝔸n и рассматриваем кольцо над алгебраически замкнутым полем, то общих точек у него было бы столько, сколько существует неприводимых аффинных подмногообразий. Обращает на себя внимание тот факт, что понятие общей точки никак, в рамках формального определения спектральной топологии, не поддается строгому определению, а лишь характеризует количество неприводимых аффинных подмногообразий. Математическое обоснование общей точки становится возможным только при реализации концепции пучков и введения математики алгебраических схем. Исторически понимание данного момента именно так и происходило.
Теперь рассмотрим вместо аффинной прямой аффинную плоскость. Тогда спектральная топология в терминах замкнутых подмножеств дает нам еще один пример. Замкнутые подмножества аффинной плоскости – это конечные объединения неприводимых кривых и точек. Соответственно, открытые подмножества получаются удалением с плоскости конечного числа кривых и точек. Любая точка в открытом подмножестве имеет в нём окрестность, полученную удалением с плоскости одной неприводимой кривой.
Топология Зарисского хотя и вполне естественна, но можно видеть, что в ней множеств, как открытых, так и замкнутых, неформально говоря, получается очень мало. Действительно, если мы находимся в рамках метрической топологии, то любое замкнутое множество в ℝn является прообразом точки при некотором непрерывном отображении аффинного пространства 𝔸n в ℝ. Но, в топологии Зарисского, любое замкнутое множество является прообразом при некотором регулярном отображении аффинных пространств 𝔸n в 𝔸m, что конечно сразу сокращает их количество. Количество открытых множеств коррелирует с данными отображениями и сокращается вместе с замкнутыми по их определению. Отметим также, что регулярные функции и отображения непрерывны в топологии Зарисского, т.е. прообраз любого открытого множества открыт, что еще раз демонстрирует естественность данной топологии, а также и тот факт, что Spec является контравариантным функтором из категории коммутативных колец в категорию топологических пространств и к нему применимы построения, которые мы делали, вводя окольцованные пространства.
Приведем теперь примеры для комплексного поля. Они показательны, поскольку для алгебраически замкнутых полей картина бывает достаточно любопытна и может отличается от произвольного поля. Впрочем, для ℂ[x], и для ℂ[x , y] мы лишь практически дословно повторим описание для аффинного пространства, а более нетривиальные рассуждения ждут нас немного дальше.
Итак, рассмотрим топологию Зарисского на 𝔸1(ℂ)=Specℂ[x]. Любой идеал кольца ℂ[x] порожден одним элементом 𝑓, и любой ненулевой многочлен 𝑓 раскладывается в произведение линейных многочленов. Поэтому любой идеал либо нулевой, либо содержится в конечном числе максимальных идеалов. А это и означает, что замкнутые множества на 𝔸1(ℂ) являются либо конечными наборами точек, либо всем множеством 𝔸1. Соответственно, открытые множества в Specℂ[x] – это пустое множество и дополнения конечных наборов максимальных идеалов. Общая точка [(0)] содержится в любом непустом открытом множестве.
В случае 𝔸2(ℂ)=Specℂ[x , y] точки 𝔸2(ℂ), которые суть простые идеалы ℂ[x , y], могут быть лишь следующих трёх типов:
(I) “Нульмерные” точки, соответствующие максимальным идеалам: ([x - a , y - b]), для a , b∈ℂ;
(II) “Одномерные” точки вида [(𝑓)], где 𝑓∈ℂ[x , y] – неприводимый многочлен;
(III) Одна “двумерная” точка [(0)].
Поэтому замкнутое подмножество 𝔸2(ℂ) – это либо вся плоскость, либо конечное число “кривых” вместе с конечным числом “нульмерных” точек. Под “кривой” здесь понимается замыкание “одномерной” точки: “одномерная” точка вида [(𝑓)] вместе со всеми нульмерными точками, лежащими на ней, т.е. со всеми максимальными идеалами, содержащими 𝑓, т.е. с точками вида ([x - a , y - b]), где 𝑓(a , b)=0.
Из этого примера мы немедленно получаем рассуждение, которое приводит Ю.И.Манин в лекциях по алгебраической геометрии относительно специализации замыканий для точек спектра и отношениях между максимальными идеалами для этих замыканий. Для данного рассуждения берется некоторая точка из спектра x∈SpecA и, в соответствии с определением, строится её замыкание (здесь обозначения соответствуют нашему формальному определению топологии Зарисского, данному ранее):
{x ̅} =⋂E⊂Px V(E) = V(⋃E ⊂ Px E) = V(Px) = {y∈SpecA ∣ Py⊃Px}.
Из данного равенства видно, что пространство {x ̅} изоморфно SpecA∕Px, и только точки, соответствующие максимальным идеалам, замкнуты, что уже нам известно из других рассуждений. Таким образом, можно говорить, что у замыкания y={x ̅} есть так называемая специализация точки, которая равносильно включению Px⊂Py. Точки спектра как бы относятся к разным уровням. На верхнем уровне находятся замкнутые точки. На следующем уровне находятся точки, специализации которых замкнуты. На i-уровне находятся точки, специализации которых принадлежат уровням с номерами меньшими или равными i−1. И, наконец, на вершине этой пирамиды находится общая точка или конечное число общих точек по количеству неприводимых компонент спектра. Мы уже говорили, что в целом, топология Зарисского в сильной степени нехаусдорфова. С точки зрения общей топологии – топологическое пространство X называется неприводимым, если любые его два непустых открытых множества имеют непустое пересечение. Чтобы понять насколько топология Зарисского нехаусдорфова, достаточно заметить, что хаусдорфово пространство, в котором имеется больше одной точки, уже не является неприводимым. Необходимое и достаточное условие неприводимости спектра раскрывает нам следующая теорема, о содержании которой нам уже известно из ранее сказанного, но доказательство пока не было сделано.
Теорема (необходимое и достаточное условие неприводимости спектра кольца). Пусть А – некоторое коммутативное кольцо и N – его нильрадикал (идеал, состоящий из всех его нильпотентов). Спектр кольца А неприводим тогда и только тогда, когда N – простой идеал.
Доказательство. Сначала докажем достаточность условия теоремы. Пусть нильрадикал N прост и x – соответствующая ему точка в спектре кольца x∈SpecA. Поскольку, являясь нильрадикалом, N содержится в любом простом идеале, то SpecA гомеоморфен Spec(A∕N), а A∕N не имеет делителей нуля, поэтому топологически SpecA неприводим.
Для доказательства необходимости предположим, что N не является простым и проверим, что Spec(A∕N) приводим, таким образом можно ограничиться случаем, когда кольцо A не содержит нильпотентов, но содержит делители нуля. Пусть элементы 𝑓,g ∈A, а их произведение 𝑓g=0, но 𝑓≠0 и g≠0. Тогда SpecA=V(𝑓)⋃V(g)=V(𝑓g). Поэтому, 𝑓 и g обращаются в нуль на замкнутых подмножествах всего спектра, вместе покрывающих всё его пространство. Для завершения доказательства осталось убедиться, что V(𝑓) и V(g) ≠ SpecA. Эти неравенства следуют из того, что 𝑓 и g не являются нильпотентами. ∎
Таким образом, для любого идеала коммутативного кольца I⊂A, замкнутое множество неприводимо тогда и только тогда когда радикал этого идеала I прост. Получаем взаимно однозначное соответствие между точками спектра x∈SpecA и неприводимыми замкнутыми подмножествами спектра. Другими словами, каждой точке x∈SpecA соответствует замкнутое множество {x ̅}, при этом x и является общей точкой этого замкнутого подмножества, по одной общей точке для каждого неприводимого замкнутого подмножества. Дальнейшее исследование приводимости и разложимости спектра, как следует ожидать, в основном использует понятие нётеровости кольца. Найти соответствующие теоремы можно практически во всех современных книгах, посвященных алгебраической геометрии. Нам же пока будет вполне достаточного уже сказанного по данному вопросу. Однако, вернёмся к нашим примерам для комплексного поля.
Очень полезный и интересный пример приводит в своих лекциях по алгебраической геометрии А.Д.Елагин. Речь в данном примере идет о кольце над комплексным полем ℂ[x , y , z , w] и идеале I этого кольца, заданного соотношениями вида I=(wy-x2, xz-y2, wz-xy). Требуется показать, что идеал I прост и поэтому спектр Spec ℂ[x , y , z , w] ∕I неприводим.
Для того чтобы это показать, мы убедимся, что кольцо ℂ[x , y , z , w]∕I является областью целостности, для чего отождествим его с другим кольцом, записанным более удобно. Геометрически речь идет о множестве в четырехмерном аффинном пространстве, заданном уравнениями:
wy = x2, xz = y2, wz = xy.
Аффинная схема, по своей сути, и есть система полиномиальных уравнений. Наивное решение, которое опускает корректность проводимых операций, системы этих уравнений состоит в том, чтобы попытаться выразить некоторые переменные друг через друга и уменьшая тем самым их количество. Из первого уравнения получаем w=x2∕y, а из второго уравнения получаем, что z=y2∕x. Третье уравнения превращается тогда в верное тождество x2y2∕(xy)=xy и у нас остается две переменных, x и y, т.е. четверка (x , y , z , w) свелась к четверке (x , y , y2∕x , x2∕y). Далее, замечаем однородность нашей системы, т.е. при умножении решения системы (x , y , z , w) на ненулевой скаляр 𝜆∈ℂ, оно останется решением. Чтобы убрать знаменатели в четверке (x , y , y2∕x , x2∕y), умножим её на xy и получим четверку (x2y , xy2, y3, x3). Теперь, для удобства, переобозначим переменные и будем писать s , t вместо x , y. Получилось преобразование (x , y , z , w) в (s2t , st2, t3, s3). Делая простую подстановку можно увидеть, что при любых s , t∈ℂ четверка в её новом виде действительно дает решение нашей системы. Вопрос о том, верно ли обратное утверждение, пока остается открытым. Попытаемся подняться на уровень выше и поймём, что означает проведенная замена переменных. Как и для любой замены переменных, речь идет о гомоморфизме колец, который действует следующим образом:
ℂ[x, y, z, w] ⟶ ℂ[s, t], где x ↦ s2t, y ↦ st2, z ↦ t3, w ↦ s3.
Тот факт, что подстановка (s2t , st2, t3, s3) в качестве (x , y , z , w) даёт решение нашей системы уравнений, означает, что построенный гомоморфизм пропускается через факторкольцо ℂ[x , y , z , w]∕I. Действительно, для этого достаточно проверить, что все элементы идеала I переходят в 0, а для этого достаточно, чтобы три образующих идеала I переходили в 0, что уже было показано выше. Поэтому наш гомоморфизм раскладывается в композицию
ℂ[x , y , z , w] ⟶ ℂ[x , y , z , w]∕I 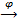 ℂ[s , t]
ℂ[s , t]
канонической проекции (вспомним теорему о гомоморфизме колец из п.1.5) и некоторого гомоморфизма 𝜑. Гомоморфизм 𝜑 позволяет связать интересующее нас кольцо ℂ[x , y , z , w]∕I с некоторым более простым для анализа кольцом вида ℂ[s , t]. Теперь следует проверить насколько гомоморфизм 𝜑 близок к изоморфизму, то есть узнать, как устроен его образ Im𝜑 и ядро Ker𝜑. Чтобы понять, как устроен образ Im𝜑, достаточно заметить, что образы – это мономы (т.е. множества с некоторой заданной ассоциативной бинарной операцией на данном множестве и существованием единицы для этой операции) общей степени 3. Поэтому образ любого многочлена от x , y , z , w содержит только мономы общей степени, которая делится на 3. Обратно, можно видеть, что любой моном от двух переменных s , t, степень которого делится на 3, лежит в образе гомоморфизма 𝜑. В результате нами описан образ гомоморфизма – это подкольцо в ℂ[s , t], состоящее из многочленов, все мономы которых имеют общую степень, делящуюся на 3. Обозначим это подкольцо через R. Далее мы сможем показать, что 𝜑 инъективен и на этом решение будет закончено, поскольку гомоморфизм 𝜑 отождествит кольцо ℂ[x , y , z , w]∕I с кольцом R, которое не содержит делителей нуля, поскольку является подкольцом в области целостности ℂ[s , t].
Для доказательства инъективности гомоморфизма 𝜑 будем использовать принятую тактику, которая не содержит слишком пристального внимания к деталям, и поступим следующим образом. Возьмем многочлен 𝑓∈ℂ[x , y , z , w] , и предположим, что его класс по модулю I переходит под действием гомоморфизма 𝜑 в 0∈ℂ[s , t]. Покажем, что из этого следует то, что класс 𝑓 по модулю I нулевой, то есть, что 𝑓∈I. Наш многочлен 𝑓 состоит из мономов вида xaybzcwd с некоторыми коэффициентами. Поскольку нас интересует только класс 𝑓 по модулю I, то для доказательства мы можем “сдвигать” 𝑓 на элементы I, т.е. свободно заменять x2 на wy, y2 на xz, wc на xy и наоборот. Каждый моном теперь можно упростить следующим образом. Если моном содержит x хотя бы во второй степени, можно x2 заменить на wy, а если он содержит y хотя бы во второй степени, то можно y2 заменить на xz. Может показаться, что мы просто ходим по кругу, ведь при избавлении от x возникает лишний y, а при избавлении от y возникает лишний x. Однако, сумма показателей степеней x и y при таких преобразованиях только уменьшается, поэтому на некотором этапе мы придем к ситуации, когда в нашем мономе xaybzcwd будут выполнены неравенства a⩽1 и b⩽1. Кроме того, если a=b=1, то можно заменить xy на zw. Таким образом, наш моном, да и вообще любой моном 𝑓, можно привести к одной из следующих трех форм:
xzcwd, yzcwd, zcwd.
Эти мономы переходят под действием гомоморфизма 𝜑 в
(s2t)t3cs3d, (st2)t3cs3d, t3cs3d, соответственно.
Далее, мы предположили, что 𝑓 переходит в 0, поэтому образ любого монома 𝑓 обязан сократиться вместе с каким-то другим мономом 𝑓’. Однако, по моному setf мы можем однозначно восстановить каким мономом он порожден из тройки xzcwd, yzcwd или zcwd, и найти c и d, что делается анализом остатков от деления e и f на 3. Поэтому, если он сократился с каким либо другим мономом, то он сократился бы еще в многочлене 𝑓, что и дает нам равенство 𝑓=0. Вот такое замечательное решение.
Обращает на себя внимание то, что образующие идеала из рассмотренного выше примера – это определители (2⨯2)-подматриц в матрице:
( 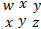 )
)
А условие равенства нулю этих определителей означает, что ранг этой матрицы не превосходит 1.
Теперь кратко обобщим все, что нам уже удалось отобразить в данном параграфе. Итак, мы поняли, как определяются аффинные схемы и спектральная топология. Что это дает нам в смысле исследования супермногообразий?
Во-первых, это восполняет чисто методологический пробел в нашем изложении. Если бы мы следовали исторической логике, то изначально не супермногообразие, а суперсхема должна была появиться в поле нашего зрения. Но, поскольку мы сразу перешли к введению супермногообразия, через математику пучков и окольцованных пространств, то и понятие суперсхемы неожиданно появилось лишь позже. Однако такая методология совершенно не принижает значимость понятия суперсхемы для суперматематики. Все утверждения, которые основываются на классической теории Гротендика, полностью суперизованы и рабочим инструментам для суперизации выступают именно суперсхемы. Об некоторых вопросах и возникающих проблемах при суперизации алгебры и геометрии, использующей аппарат суперсхем, мы будем еще много говорить далее.
Во-вторых, нам концептуально важна именно геометрия супермногообразия, а не прикладные проблемы, возникающие в суперизации алгебраической геометрии и которые обычно приводят к исследованию супералгебр. Вот почему мы сделали определение суперсхем уже после того, как дали определение супермногообразия.
Добавим, что понятие схемы и было предложено Гротендиком, чтобы осуществить возможность применения пучков для исследования алгебраических многообразий. Точка аффинного многообразия при таком подходе нашла свою двойственную интерпретацию как максимальный идеал координатного кольца. Соответственно точки аффинной суперсхемы стали двойственно интерпретироваться как простые идеалы соответствующего кольца. Говоря категорным языком, аффинные схемы образуют категорию, двойственную к категории коммутативных колец, а оперирование нётеровостью колец позволяет делать утверждения, которые раньше были неразрешимы сразу для целых классов задач. Склейки аффинных схем, превращающих их в глобальные (или общие) схемы стало возможным осуществлять как склейки топологических пространств (с топологией Зарисского), что и позволило добиться таких важных результатов в алгебраической геометрии. Учитывая важность всего сказанного, далее мы дадим современное определение схемы, а также сформулируем и докажем две теоремы Гильберта, о которых уже упоминалось выше – теорему о базисе и теорему о нулях – чтобы понимание вопросов, связанных с теорией схем, нётеровостью колец и спектральной топологией стало еще более наглядным.
Современное определение схем и суперсхем, по существу, ничем не отличается от уже сделанного нами определения через модельные категории и вводится следующим образом. Пусть 𝜑:A⟶B – гомоморфизм колец. Прообраз 𝜑-1(P) каждого простого идеала P⊂B прост, поэтому гомоморфизм 𝜑 задает отображение
𝜑* : SpecB ⟶ SpecA, 𝜑*(P) = 𝜑 -1(P).
Для данного отображения справедливо соотношение (𝜑𝜓)* = 𝜓*∘𝜑*, а также то, что 𝜑* непрерывно относительно топологии Зарисского на SpecB и SpecA, что следует из следующей цепочки утверждений, показывающей, что прообраз замкнутого множества замкнут:
y∈V(𝜑(E)) ⟺ 𝜑(E)⊂𝜑-1(Py)=P𝜑*(y) ⟺ 𝜑*(y)∈V(E) ⟺ y∈(𝜑*)-1(V(E)).
Следовательно, сопоставление Spec:Ring°⟶Top является контравариантным функтором из категории колец (или суперколец, в случае суперкоммутативности) в категорию топологических пространств. Тройка (X, 𝛼, A), где X – топологическое пространство, а 𝛼:X⟶SpecA – изоморфизм топологических пространств, называется аффинной предсхемой, а морфизмом (Y, 𝛽, B)⟶(X, 𝛼, A) аффинных предсхем называется пара (𝑓, 𝜑), где 𝑓:X⟶Y – непрерывное отображение, а 𝜑:A⟶B – гомоморфизм колец, такой, что следующая диаграмма является коммутативной:
Y 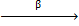 SpecB
SpecB
𝑓 𝜑*
X 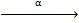 SpecA
SpecA
Вообще, можно избежать понятия предсхемы и просто указать, что рассмотрена аффинная схема, в определении которой пока не задействовано понятие пучка, т.е. сделано, так сказать, предварительное определение. Теперь перейдем к полному определению. Из §.2.1. вспомним, что если J – простой идеал в кольце А, то выбрав в качестве мультипликативной системы S разность A–J, мы получаем в качестве кольца частных AS локальное кольцо идеала J. Аффинной схемой мы назвали локально окольцованное пространство (SpecA=X, Q(X)), где росток Q(X)x в точке x∈SpecA – локальное кольцо соответствующего простого идеала, т.е. кольцо частных AS, где S=A–x. Будем рассматривать теперь не точку, а окрестность точки x (т.е. перейдем к рассмотрению ростков окрестностей этой точки), тогда соответствующий пучок обозначим через Ã. Суперокольцованным пространством будем в рамках данного определения схемы называть пару (X, ℱ), где X – топологическое пространство, а ℱ – пучок супералгебр на X.
Морфизмом суперокольцованных пространств ω:(X, ℱ)⟶(Y, 𝒢), назовем пару (ῶ,{ω*U│U⊂Y}) состоящую из непрерывного отображения ῶ:X⟶Y и набора гомоморфизмов супералгебр ω*U:𝒢(U)⟶ℱ(ῶ-1(U)), определенного для каждой пары открытых подмножеств U⊂Y и согласованного с отображениями ограничения
(ρ│ῶ-1(V)⟶ῶ-1(U) ) ∘ ω*V = ω*U ∘ ( ρ│V⟶U)
для любых открытых множеств U⊂V⊂X.
Аффинная предсхема становится схемой в соответствии со следующим определением. Окольцованное пространство, изоморфное одному из (SpecA, Ã), где А – коммутативное кольцо, называется аффинное схемой. Суперокольцованное пространство, изоморфное одному из (SpecA, Ã), где А – суперкоммутативное кольцо, называется аффинной суперсхемой. Ну и теперь вполне естественно определить, что окольцованное топологическое пространство (X, QX), локально изоморфное аффинной схеме, называется схемой (или – общей схемой). Суперокольцованное топологическое пространство (X, QX), локально изоморфное аффинной суперсхеме, называется суперсхемой. Суть разницы между классическим и супер случаем состоит в устройстве морфизмов для окольцованных пространств. Дело в том, что для классических окольцованных пространств – это произвольные гомоморфизмы алгебр, даже если пучки – это пучки супералгебр. Но морфизмы тех же объектов, рассмотренные в категории суперокольцованных пространств, должны сохранять четность. Таков современный подход к определению схем и суперсхем.
Теперь вернёмся к теоремам Гильберта. Теорема Гильберта о базисе решила проблему для колец многочленов, которая состояла в том, что нётеровость кольца многочленов над другим кольцом каждый раз проверялась отдельно.
Теорема (Теорема Гильберта о базисе). Если кольцо А – нётерово, то кольцо многочленов A[x] – тоже нётерово.
Доказательство. Пусть I⊂A[x] – идеал. Рассмотрим множество I0⊂A, состоящее из старших коэффициентов многочленов, входящих в кольцо А. Ясно, что I0 – идеал в А. Это следует из того, что т.к. 𝑓(x)=axn+…∈I, g(x)=bxm+…∈I, следовательно 𝑓(x)xm+g(x)xn=(a+b)xn+m+…∈I, c𝑓(x)=caxn+…∈I, следовательно, a+b∈I0, ca∈I0 для всех c∈A. Идеал I0 конечно порожден над кольцом А. Выберем конечный набор образующих a1,…,an идеала I0 над A и пусть 𝑓1,…,𝑓n ∈ A[x] – многочлены из I, старшие коэффициенты которых равны a1,…,an. Пусть N = max deg 𝑓i. Пусть далее M=I⋂A〈1,x,…,xN-1〉⊂A[x]. Тогда M является А-подмодулем в свободном А-модуле конечного ранга (т.е. модуле, который обладает базисом – непустой системой элементов, являющейся линейно независимой и порождающей этот модуль), и, значит, модуль М конечно порожден над А.
Выберем конечный набор образующих g1,…,gm модуля М над А и докажем, что многочлены 𝑓1,…,𝑓n,g1,…,gm порождают идеал I над A[x]. Для этого надо любой многочлен h(x)∈I представить в виде линейной комбинации многочленов 𝑓i,g j. Действительно, если степень многочлена deg h < N, то h∈M и представляется в виде линейной комбинации многочленов g j. Пусть теперь степень многочлена deg h > N, h=axk+….
Тогда a ∈ I0, значит a = ∑ciai, ci∈A, следовательно, если h′(x) = h(x) − ∑cixk-deg𝑓i 𝑓i, то h′(x)∈I, причем deg h′ < deg h.
Повторяя это рассуждение, заключаем, что h представляется в виде линейной комбинации многочленов 𝑓i и многочлена, лежащего в идеале I, степень которого меньше, чем N. ∎
Из Теоремы Гильберта о базисе мы немедленно получаем четыре важных следствия (с некоторыми мы уже знакомы) над конечно порожденным полем (или полем Галуа) 𝕂 – остановимся в этих следствиях именно на таких полях:
(I) Кольцо многочленов 𝕂[x1,…,xn] нётерово;
(II) Любая конечно порожденная коммутативная 𝕂-алгебра нётерова;
(III) Если кольцо А нётерово, то любая конечно порожденная коммутативная А-алгебра нётерова;
(IV) Любой идеал в конечно порожденной коммутативной 𝕂-алгебре конечно порожден.
И, наконец, перейдем к концептуальной для алгебраической геометрии теореме – теореме Гильберта о нулях, которое было им впервые опубликовано в 1893 году. Мы сделаем классическое доказательство (классическое – в смысле использования классических категорий) этой теоремы и затем рассмотрим трактовку её доказательства с точки зрения спектральной топологии. Первое, что будет для нас важно – это алгебраическая замкнутость поля в формулировке теоремы. Чтобы продемонстрировать важность алгебраической замкнутости поля, рассмотрим идеал в кольце ℝ[x], порожденный А≔(x2+1)ℝ[x]⊂ℝ[x]. Замкнутое подмножество V(A)⊂ℝ задается уравнением x2+1=0, которое не имеет вещественных решений. Поэтому V(A)=∅ и идеал IV(A)=ℝ[x], но, с другой стороны радикал кольца R(A)≠ℝ[x]. Причина в том, что V(A) не имеет вещественных точек, но имеет две комплексные точки i и -i, поэтому при переходе к полю ℂ получаем V(A)={i, -i} и IV(A)={𝑓(x)∊ℂ[x] │(x - i)∣𝑓(x), (x + i)∣𝑓(x)} = {𝑓(x)∊ℂ[x] │ (x2+1)∣𝑓(x)}=A. Этот пример иллюстрирует нам следующий важный принцип – алгебраическое многообразие над незамкнутым полем следует рассматривать как множество точек соответствующего многообразия над алгебраически замкнутым расширением этого поля, имеющих координаты в первоначальном незамкнутом поле. Существует, так называемая слабая форма теоремы Гильберта о нулях, утверждающая, что всякий максимальный идеал в алгебре функций на аффинном алгебраическом многообразии X имеет вид Ix, x∊X. В этой формулировке условие алгебраической замкнутости поля также существенно, поскольку идеал А, рассмотренный выше, максимален, т.е. ℝ[x]∕A≅ℂ. Однако, чтобы его представить в виде Ix, надо в качестве точки x взять точку с комплексными координатами.
Пусть X – алгебраическое многообразие, 𝕂 – некоторое поле и 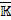 – его алгебраически замкнутое расширение. Через 𝕂[X] – обозначим множество регулярных (см. определение в п.2.1.) функций, это множество является коммутативным кольцом и содержит в себе поле 𝕂, его называют кольцом или алгеброй регулярных функций на X. И пусть радикал идеала I⊂A в коммутативном кольце A, по определению, будет множество R(I) элементов a∊A таких, что aN∊I для некоторого N∊ℕ. При равенстве R(I)=I идеал I называется радикальным. Выпишем основные свойства радикала, которые нам потребуются и которые либо нам уже известны, либо просто следуют из определений:
– его алгебраически замкнутое расширение. Через 𝕂[X] – обозначим множество регулярных (см. определение в п.2.1.) функций, это множество является коммутативным кольцом и содержит в себе поле 𝕂, его называют кольцом или алгеброй регулярных функций на X. И пусть радикал идеала I⊂A в коммутативном кольце A, по определению, будет множество R(I) элементов a∊A таких, что aN∊I для некоторого N∊ℕ. При равенстве R(I)=I идеал I называется радикальным. Выпишем основные свойства радикала, которые нам потребуются и которые либо нам уже известны, либо просто следуют из определений:
(I) Радикал идеала является идеалом;
(II) R(I)⊃I;
(III) R(R(I)) = R(I);
(IV) R(I1 ⋂ I2) = R(I1) ⋂ R(I2);
(V) Если идеал I прост, то радикал R(I) = I;
(VI) Если ∩J – пересечение простых идеалов, то R(∩J) = ∩J.
Так что же мы желаем показать, доказывая теорему Гильберта о нулях? Собственно, именно то, с чего мы начинали данный параграф – переносом одного из важных фактов для геометрии объектов в категории алгебраических многообразий на алгебраический язык. Мы уже поняли, что для аффинных многообразий алгебра функций 𝕂[X] содержит всю информацию о многообразии X. Более того, алгебра функций является гораздо более удобной для исследования, а в отношении супер случая и вообще – единственной математической альтернативой, которая может быть исследована, если речь идет о геометрических свойствах супермногообразия. Польза алгебры функций также вытекает из того замечательного факта, что для проективных многообразий она состоит из функций, постоянных на каждой компоненте связности и таким образом тривиальна для исследования. Ко всему, мы на данном этапе, вполне понимаем, что алгебру функций для аффинных многообразий несложно вычислить. Действительно, если X⊂𝔸n аффинное многообразие над полем 𝕂, то имеется сюръективный гомоморфизм ограничения 𝕂[x1,…,xn]→𝕂[X]. Его ядро, по определению, является идеалом I многообразия X, поэтому мы имеем канонический изоморфизм (см. теорему о гомоморфизме колец из §.1.5) 𝕂[X] ≅ 𝕂[x1,…,xn]∕I(X).
В то же время, если Y⊂X – подмногообразие в аффинном многообразии X, то мы можем рассмотреть идеал IX(Y) в 𝕂[X], состоящий из всех функций, тождественно обращающихся в ноль на Y и, естественно, что разным подмногообразиям будут соответствовать разные идеалы, т.к. всякое подмногообразие восстанавливается по своему идеалу как множество нулей в X всех его функций. Другими словами, алгебраические подмногообразия в X однозначно соответствуют некоторым идеалам в 𝕂[X]. И теорема Гильберта о нулях дает нам способ описания таких идеалов. Далее мы будем, для удобства, все утверждения доказательной группы данной теоремы помечать через Nss от немецкого названия теоремы Nullstellensatz. Одна из формулировок теоремы может быть записана следующим образом:
Теорема (теорема Гильберта о нулях, формулировка I , 1, Nss). Пусть поле 𝕂 алгебраически замкнуто, X⊂𝔸n аффинное многообразие над полем 𝕂 и J⊂𝕂[X] – идеал. Тогда идеал замкнутого подмножества этого идеала равен радикалу данного идеала, т.е. имеет место равенство I(V(J))=R(J).
В данной формулировке мы использовали два отображения между множеством подмножеств (и не обязательно алгебраических!) в X и множеством идеалов в 𝕂[X], Мы просто сопоставили подмножеству Y⊂X идеал
I(Y) = { 𝑓∈ 𝕂[X] │ 𝑓∣Y = 0}.
И идеалу мы сопоставили подмножество (замкнутое по определению в топологии Зарисского, поэтому мы продолжаем использовать обозначение V из определения топологии Зарисского)
V(J) = {x∈X │∀𝑓∈J 𝑓(x)=0}.
Отображения I(Y) и V(J) не взаимно обратны, но они взаимно обратны на своих образах. Таким образом, теорема Гильберта говорит, что I(V(J)) – радикал идеала и, следовательно, образ отображения I – радикальный идеал, поэтому мы немедленно получаем:
Следствие (2, Nss ). Если поле 𝕂= 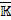 , то имеется взаимно однозначное соответствие между аффинными подмногообразиями в аффинном многообразии X и радикальными идеалами в алгебре 𝕂[X]. ∎
, то имеется взаимно однозначное соответствие между аффинными подмногообразиями в аффинном многообразии X и радикальными идеалами в алгебре 𝕂[X]. ∎
Более простыми словами теорему Гильберта о нулях также можно сформулировать следующим образом:
Теорема (теорема Гильберта о нулях, формулировка II , 3, Nss) Пусть поле 𝕂 алгебраически замкнуто и 𝑓, 𝑓1,…, 𝑓m∈𝕂[x1,…,xn] – многочлены. Пусть 𝑓 обращается в ноль во всех точках 𝔸n над полем 𝕂, где обращаются в ноль все 𝑓i. Тогда при некотором N∊ℕ многочлен 𝑓N представляется в виде 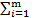 𝑓igi, где gi∈𝕂[x1,…,xn] – многочлены.
𝑓igi, где gi∈𝕂[x1,…,xn] – многочлены.
Но прежде, чем перейти к доказательству теоремы Гильберта о нулях нам потребуется небольшая подготовительная работа. Она нам будет полезна не только для доказательства, но и потому, что мы еще раз сможем увидеть в сути данной подготовки, насколько естественно использование понятия пучка для алгебраического метода. Еще раз подчеркнем, что все дальнейшие рассуждения проводятся для объектов категории аффинных алгебраических многообразий над замкнутым полем, но крайне полезно будет представлять (пусть даже интуитивно) возможные обобщения, т.е. предполагать существование функторов в нужные категории и, в первую очередь, не забывать о существовании двойственной для нее категории коммутативных колец. Кроме того, некоторые факты из подготовительной работы, в целом, нам уже известны и не требуют тщательного анализа.
Предложение (4, Nss ). Для того чтобы аффинное многообразие X было неприводимо необходимо и достаточно, чтобы в кольце 𝕂[X] не было делителей нуля.
Доказательство. Сначала покажем необходимость нашего условия. Доказывать будем от противного. Допустим, что существуют делители нуля 𝑓1𝑓2=0. Тогда получаем, что имеет место разложение многообразия X в объединение X={𝑓1=0}∪{𝑓2=0} и значит наше многообразие приводимо, что противоречит условию о неприводимости X.
Достаточность следует из того, что если разложение X=X1∪X2 нетривиально, то найдутся функции 𝑓i такие, что 𝑓i∣Xi=0 и 𝑓i≠0. Но значит, что 𝑓1𝑓2=0 и кольцо 𝕂[X] содержит делители нуля, что противоречит условию. ∎
Следствие (5, Nss ). Пусть Y⊂X – аффинное подмногообразие. Идеал I(Y)⊂𝕂[X] прост тогда и только тогда, когда подмногообразие Y неприводимо.
Доказательство. Подмногообразие Y неприводимо тогда и только тогда, когда кольцо 𝕂[Y]=𝕂[X]∕I(Y) не имеет делителей нуля, что, в свою очередь, выполнимо (по определению) тогда и только тогда, когда идеал I(Y) прост. ∎
Предложение (6, Nss ). Пусть X – аффинное многообразие, а J⊂𝕂[X] – радикальный идеал. Тогда J = 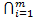 Pi является пересечением некоторых простых идеалов Pi.
Pi является пересечением некоторых простых идеалов Pi.
Доказательство. Многообразие Y = V(J) раскладывается в объединение своих неприводимых компонент Y = 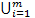 Yi.
Yi.
Переходя к идеалам и используя следствие(2, Nss) мы можем записать, что радикальный идеал
J = R(J) = I(V(J)) = I(⋃Yi) = ⋂I(Yi).
А идеалы Pi = I(Yi) простые по следствию (5, Nss), что и доказывает данное предложение. ∎
С точки зрения теории пучков, нам важно отметить здесь уже известный нам факт, что композиция регулярных отображений регулярна. Пусть у нас имеется регулярное отображение аффинных многообразий 𝜙:X→Y. Это отображение определяет естественный гомоморфизм алгебр функций 𝜙*: 𝕂[Y] → 𝕂[X] по следующему правилу. Если функция 𝑓∈𝕂[Y], то 𝜙*𝑓=𝑓∘𝜙. Понятно, что для композиции отображений X 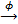 Y
Y 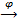 Z будем иметь место равенство (𝜑𝜙)*=𝜙*𝜑*. Следующее предложение устанавливает связь между гомоморфизмом алгебр и тем, как выглядит этот гомоморфизм для регулярного отображения аффинных многообразий. Более того, само регулярное отображение в таком случае будет единственным.
Z будем иметь место равенство (𝜑𝜙)*=𝜙*𝜑*. Следующее предложение устанавливает связь между гомоморфизмом алгебр и тем, как выглядит этот гомоморфизм для регулярного отображения аффинных многообразий. Более того, само регулярное отображение в таком случае будет единственным.
Предложение (о гомоморфизме алгебр для регулярных отображений, 7, Nss ). Пусть 𝜇: 𝕂[Y] → 𝕂[X] – гомоморфизм алгебр над замкнутым полем 𝕂. Тогда он имеет вид 𝜙*: 𝕂[Y] → 𝕂[X] для единственного регулярного отображения 𝜙:X→Y.
Доказательство. Пусть Y⊂𝔸m, yi – координатные функции на 𝔸m. Обозначим через 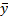 i∈ 𝕂[Y] – их ограничения на Y и положим
i∈ 𝕂[Y] – их ограничения на Y и положим
𝜙(x) = (𝜇( 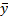 1)(x),…, 𝜇(
1)(x),…, 𝜇( 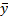 m)(x)).
m)(x)).
Так как 𝜇( 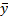 i) – регулярные функции на X, то отображение 𝜙 регулярно по определению. Проверим, что образ Im𝜙⊂Y. Пусть 𝑓∈I(Y) – многочлен. Покажем, что 𝑓 обнуляется на образе Im𝜙. Действительно,
i) – регулярные функции на X, то отображение 𝜙 регулярно по определению. Проверим, что образ Im𝜙⊂Y. Пусть 𝑓∈I(Y) – многочлен. Покажем, что 𝑓 обнуляется на образе Im𝜙. Действительно,
𝑓 (𝜇( 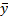 1)(x),…, 𝜇(
1)(x),…, 𝜇( 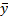 m)(x)) = 𝜇(𝑓(
m)(x)) = 𝜇(𝑓( 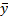 1,…,
1,…, 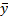 m))(x) = 𝜇(0)(x) = 0.
m))(x) = 𝜇(0)(x) = 0.
Также понятно, что 𝜙*=𝜇 на всех 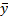 i и значит на всей алгебре функций 𝕂[Y]. Единственность 𝜙 следует из того, что если бы это было не так, то существовал бы еще одно отображение 𝜗, для которого выполнялось бы равенство 𝜗*𝑓 = 𝑓∘𝜗, и для которого 𝑓 обнулялся уже на образе Im𝜗. Но 𝜇 гомоморфизм алгебр, а не произвольных колец. И, следовательно, разность между отображениями 𝜙*𝑓 и 𝜗*𝑓 должна была бы лежать в идеале, который для отображения алгебр тривиальный. ∎
i и значит на всей алгебре функций 𝕂[Y]. Единственность 𝜙 следует из того, что если бы это было не так, то существовал бы еще одно отображение 𝜗, для которого выполнялось бы равенство 𝜗*𝑓 = 𝑓∘𝜗, и для которого 𝑓 обнулялся уже на образе Im𝜗. Но 𝜇 гомоморфизм алгебр, а не произвольных колец. И, следовательно, разность между отображениями 𝜙*𝑓 и 𝜗*𝑓 должна была бы лежать в идеале, который для отображения алгебр тривиальный. ∎
Следствие (8, Nss ). Пусть 𝜙:X→Y – регулярное отображение между аффинными многообразиями и 𝜙* – изоморфизм, тогда и 𝜙 – изоморфизм.
Далее, пусть алгебры 𝕂[X] и 𝕂[Y] изоморфны, тогда и аффинные многообразия X и Y тоже изоморфны. ∎
Предложение (9, Nss ). Подмногообразия аффинных многообразий соответствуют сюръективным гомоморфизмам алгебр функций.
Доказательство. Пусть X⊂Y – аффинное подмногообразие. Любая регулярная функция на X является ограничением многочлена с аффинного пространства, а значит, и является ограничением регулярной функции с Y. Поэтому мы имеем сюръекцию 𝕂[Y] → 𝕂[X], поскольку данной отображение является ограничением.
Обратно, пусть мы имеем сюръективный гомоморфизм 𝜙*: 𝕂[Y] → 𝕂[X] и пусть I=Ker𝜙* – его ядро. Пусть подмногообразие X'⊂Y является множеством нулей всех функций из I. Тогда образ Im𝜙 лежит в X', и если 𝑓∈I(X'), то 𝜙(𝑓)=0, поэтому 𝑓∈I. Значит I=I(X') и для отображения 𝜑:X → X' имеем 𝜑*: 𝕂[X']=𝕂[Y]∕I→𝕂[X] – изоморфизм. Используя утверждения следствие (8, Nss), получаем, что 𝜑* – изоморфизм, т.е. X – подмногообразие. ∎
Приведем пример, который дает большее понимание последнего предложения. Пусть у нас есть два аффинных многообразия разной размерности, а отображения между ними задаются параметрически. Например, пусть X=𝔸1, Y=𝔸2 и отображение 𝜙(t)=(t2, t3). Тогда 𝜙*(x)=t2, 𝜙*(y)=t3. Образ Im𝜙* является подкольцом𝕂[t2, t3]⊂𝕂[t], поэтому 𝜙* не сюръективно. И хотя отображение 𝜙 является инъективным на множестве точек, оно, однако, не является вложением подмногообразия, поскольку его образ не изоморфен 𝔸1.
Напомним, что подмножество M топологического пространства X называется плотным, если его замыкание 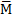 совпадает со всем пространством X. Если быть более аккуратным в определениях, то первое множество А называется плотным во втором множестве B, если замыкание первого множества содержит второе множество. Подразумевается, что любая окрестность точки b из множества B содержит элемент из A, или, иначе говоря, элементы А сколько угодно близко приближаются к любому элементу из B. Когда речь идет не о множестве, по отношению к которому производится замыкание, а об объемлющем топологическом пространстве, то говорят о всюду плотном множестве. Множество называется всюду плотным в некотором пространстве, если его замыкание совпадает со всем этим пространством. Но поскольку здесь нет единого подхода в определениях, будем плотное и всюду плотное множества называть плотными. Пример – множество рациональных чисел ℚ плотно в пространстве вещественных чисел ℝ. В отношении топологии Зарисского имеется одно, достаточно удивительное утверждение, касающееся образа отображения аффинных многообразий, а значит, и дополнительно проясняющее нам его устройство.
совпадает со всем пространством X. Если быть более аккуратным в определениях, то первое множество А называется плотным во втором множестве B, если замыкание первого множества содержит второе множество. Подразумевается, что любая окрестность точки b из множества B содержит элемент из A, или, иначе говоря, элементы А сколько угодно близко приближаются к любому элементу из B. Когда речь идет не о множестве, по отношению к которому производится замыкание, а об объемлющем топологическом пространстве, то говорят о всюду плотном множестве. Множество называется всюду плотным в некотором пространстве, если его замыкание совпадает со всем этим пространством. Но поскольку здесь нет единого подхода в определениях, будем плотное и всюду плотное множества называть плотными. Пример – множество рациональных чисел ℚ плотно в пространстве вещественных чисел ℝ. В отношении топологии Зарисского имеется одно, достаточно удивительное утверждение, касающееся образа отображения аффинных многообразий, а значит, и дополнительно проясняющее нам его устройство.
Предложение (о плотности образа отображения в топологии Зарисского, 10, Nss ). Чтобы отображение двух аффинных многообразий 𝜙:X→Y имело плотный в топологии Зарисского образ необходимо и достаточно, чтобы гомоморфизм 𝜙* был инъективным.
Другими словами, при инъективности 𝜙*: 𝕂[Y] → 𝕂[X] мы имеем 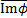 =Y.
=Y.
Доказательство. Начнем с условия необходимости. Если 𝜙* имеет нетривиальное ядро, т.е. 𝜙*: 𝕂[Y] → 𝕂[X] не является инъективным, то тогда возьмем функцию 𝑓∈𝕂[Y], такую что 𝜙*𝑓=0. Тогда образ Im𝜙, а значит и его замыкание 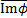 , лежит в замкнутом подмножестве {y │ 𝑓(y)=0}⊂Y и потому не плотен в Y.
, лежит в замкнутом подмножестве {y │ 𝑓(y)=0}⊂Y и потому не плотен в Y.
Достаточность следует из того, что если предположить обратное, т.е. что замыкание образа 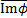 ≠Y, то найдется ненулевая функция 𝑓∈𝕂[Y] такая, что 𝑓=0 на всем 𝜙(Y). Что, в свою очередь, означает, что ядро Ker 𝜙* нетривиально и значит, гомоморфизм 𝜙* не является инъективным. ∎
≠Y, то найдется ненулевая функция 𝑓∈𝕂[Y] такая, что 𝑓=0 на всем 𝜙(Y). Что, в свою очередь, означает, что ядро Ker 𝜙* нетривиально и значит, гомоморфизм 𝜙* не является инъективным. ∎
Приведем пример для двухмерных аффинных многообразий. Пусть X=Y=𝔸2 и задано отображение 𝜙(u, v)=(u, uv). Тогда 𝜙*(x)=u, 𝜙*(y)=uv, и 𝜙* является инъективным. При этом образ Im𝜙 состоит из точек (x, y), для которых x≠0, а также точки (0, 0). Этот образ не замкнут и не открыт, но его замыкание совпадает со всем пространством и поэтому данный образ плотен.
А если задать отображение 𝜑(u, v)=(u-v, (u-v)2), то 𝜑*(x2-y)=0, т.е. не инъективно. Образ отображения Im𝜑 является параболой на плоскости, и она не является плотным множеством.
Предложение (11, Nss ). Вложения многообразия X в аффинное пространство соответствуют системам образующих в алгебре 𝕂[X].
Доказательство. Если мы имеем вложение многообразия X⊂𝔸n, то ограничения координатных функций 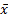 i ∈ 𝕂[X] порождают алгебру 𝕂[X].
i ∈ 𝕂[X] порождают алгебру 𝕂[X].
Обратно, системе порождающих e1,…,en∈𝕂[X] соответствует сюръективный гомоморфизм 𝕂[x1,…,xn]⟶𝕂[X], и следовательно, используя предложение (9, Nss), мы имеем вложение многообразия X⊂𝔸n. ∎
Подготовительная работа для доказательства теоремы Гильберта о нулях на этом завершена. Теперь мы сделаем еще одну, так называемую – чисто алгебраическую формулировку этой теоремы и сразу докажем два важных следствия, а затем сделаем доказательство самой теоремы, но не для алгебраической версии, а для второй её формулировки (3, Nss). Алгебраическая версия теоремы Гильберта о нулях является нетривиальным следствием классической формулировки, и мы оставим данную версию без доказательства.
Теорема (теорема Гильберта о нулях, формулировка III , алгебраическая версия, 12, Nss). Пусть А – конечно порожденное кольцо над полем 𝕂, само являющееся полем. Тогда А – конечное расширение поля 𝕂, т.е. конечномерно над полем 𝕂.
Сразу коснемся вопроса применимости. Именно алгебраическая формулировка теоремы Гильберта о нулях дает нам быстрый способ понять, почему для некоторых колец мы не можем получить конструктивные результаты. Применимость разберем на двух примерах.
(I) Пусть А – является кольцом многочленов для элемента x, т.е. A=𝕂[x]. Тогда А конечно порождена над полем 𝕂 как алгебра. Но А – не является полем. Поэтому теорема неприменима, и А – не конечно порожденный модуль над полем 𝕂.
(II) Пусть А – является кольцом функций для элемента x, т.е. A=𝕂(x). Тогда А – является полем. Но A является не конечно порожденной, как алгебра. Поэтому теорема неприменима, и А – не конечно порожденный модуль над полем 𝕂.
Всё это желает большей проработки и объяснения, и мы, без сомнения, сделаем это в дальнейшем, но уже и так ясно, что есть детали, заключенные в условии, которые многое нам могут прояснить. Так, одним из интересных фактов, является лемма о том, что поле нулевой характеристики не может быть алгеброй конечного типа над кольцом целых чисел. Утверждение вполне очевидное, но требующее для своего доказательства применения леммы Нётер о нормализации. Поэтому, на данном этапе мы оставим этот вопрос без подробного рассмотрения и продолжим нашу работу в рамках классического доказательства.
Следствие (13, Nss ). Пусть J – собственный идеал 𝕂[x1,…,xn] и 𝕂= 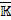 . Тогда замкнутое в топологии Зарисского множество V(J) = {x∈X │∀𝑓∈J 𝑓(x)=0} не является пустым.
. Тогда замкнутое в топологии Зарисского множество V(J) = {x∈X │∀𝑓∈J 𝑓(x)=0} не является пустым.
Доказательство. Пусть J=𝕂[x1,…,xn] – собственный идеал. Его можно вложить в максимальный идеал 𝔐. Он имеет вид 𝔐=J(p) для некоторой точки p∈𝔸n. Тогда данная точка p содержится в V(J), p∈V(J). Действительно, если 𝑓∈J, то 𝑓∈J(p) и 𝑓(p)=0. Следующее следствие дополнительно объяснит наши рассуждения. ∎
Следствие (14, Nss ). Пусть поле алгебраически замкнуто 𝕂= 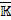 . Тогда все максимальные идеалы в кольце A=𝕂[x1,…,xn] имеют вид I(p)=(x1-a1,…,xn-an) для некоторой точки p=(a1,…,an)∈𝔸n.
. Тогда все максимальные идеалы в кольце A=𝕂[x1,…,xn] имеют вид I(p)=(x1-a1,…,xn-an) для некоторой точки p=(a1,…,an)∈𝔸n.
Доказательство. Воспользуемся удобным критерием: идеал I⊂R максимален тогда и только тогда, когда факторкольцо R∕I является полем.
Сначала проверим, что идеалы из условия максимальны.. Пусть p=(a1,…,an) – точка, рассмотрим гомоморфизм 𝕂[x1,…,xn]→𝕂, переводящий 𝑓 в 𝑓(p). Он сюръективный и его ядро – это идеал I(p). Тогда мы имеем изоморфизм A∕I(p)≅𝕂 из которого следует, что I(p) максимален.
Обратно, пусть 𝔐⊂A – максимальный идеал. Тогда поле 𝔽=A∕𝔐 содержит поле 𝕂 и это поле 𝔽 конечно порождено над 𝕂 как алгебра, что следует их того, что алгебра A конечно порождена. Значит, по алгебраической версии теоремы Гильберта о нулях, поле 𝔽 – это конечное расширение поля 𝕂. Но 𝕂 алгебраически замкнуто по условию, поэтому 𝔽=𝕂. Пусть элементы 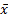 i∈𝔽, являющиеся образами элементов xi∈A, соответствуют числам ai∈𝕂. Тогда образы xi-ai в 𝔽 равны нулю и xi-ai∈𝔐. Следовательно, I(p)=(x1-a1,…,xn-an)∈𝔐. Из максимальности I(p) получаем, что I(p)=𝔐. ∎
i∈𝔽, являющиеся образами элементов xi∈A, соответствуют числам ai∈𝕂. Тогда образы xi-ai в 𝔽 равны нулю и xi-ai∈𝔐. Следовательно, I(p)=(x1-a1,…,xn-an)∈𝔐. Из максимальности I(p) получаем, что I(p)=𝔐. ∎
Этот факт мы используем при переходе от подмножеств аффинного пространства, т.е. от подмножества его точек, к целостной сущности – аффинным многообразиям.
Доказательство (теорема Гильберта о нулях, формулировка II, 3, Nss). Пусть X⊂𝔸n замкнутое алгебраическое подмножество аффинного пространства задано уравнениями 𝑓1= …= 𝑓m=0, и 𝑓∣X=0. Рассмотрим подмножество 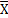 ⊂ 𝔸n+1, заданное уравнениями
⊂ 𝔸n+1, заданное уравнениями
𝑓i(x1, … , xn) = 0 и xn+1𝑓(x1, … , xn) − 1= 0.
Понятно, что 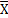 пусто: если 𝑓i(x1, … , xn) = 0, то xn+1𝑓(x1, … , xn)−1 = −1 ≠ 0. Значит по следствию (13, Nss) многочлены 𝑓i(x1, … , xn) и xn+1𝑓(x1, … , xn)–1 порождают всё кольцо 𝕂[x1,…, xn+1]. Мы можем записать равенство
пусто: если 𝑓i(x1, … , xn) = 0, то xn+1𝑓(x1, … , xn)−1 = −1 ≠ 0. Значит по следствию (13, Nss) многочлены 𝑓i(x1, … , xn) и xn+1𝑓(x1, … , xn)–1 порождают всё кольцо 𝕂[x1,…, xn+1]. Мы можем записать равенство
1 = b(x1, …, xn+1)( xn+1𝑓(x1, … , xn)–1) + ∑ai(x1, … , xn+1) 𝑓i(x1, … , xn)
Суммирование идет по индексу i. Пусть N – максимальная степень, с которой xn+1 входит в многочлены ai(x1, … , xn+1), тогда умножим обе части нашего равенства на 𝑓(x)N получим
𝑓(x)N = 𝑓(x)Nb(x)( xn+1𝑓(x)–1) + ∑ 𝑓(x)N ai(x1, … , xn+1) 𝑓i(x1, … , xn).
В ai для всех встречающихся выражений с 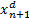 заменим все выражения вида
заменим все выражения вида 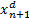 𝑓d на 1 + (
𝑓d на 1 + ( 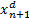 𝑓d – 1) = 1 + (xn+1𝑓–1)(…). Сделаем перенос (xn+1𝑓–1)(…) в слагаемое, где b(x)( xn+1𝑓(x)–1) и получим равенство
𝑓d – 1) = 1 + (xn+1𝑓–1)(…). Сделаем перенос (xn+1𝑓–1)(…) в слагаемое, где b(x)( xn+1𝑓(x)–1) и получим равенство
𝑓(x1, … , xn)N = 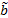 (x)( xn+1𝑓(x1, … , xn)–1) + ∑
(x)( xn+1𝑓(x1, … , xn)–1) + ∑ 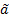 i(x1, … , xn) 𝑓i(x1, … , xn).
i(x1, … , xn) 𝑓i(x1, … , xn).
Здесь 𝑓(x)N и все слагаемые суммы не содержат координаты xn+1, а выражение 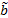 (x)( xn+1𝑓(x1, … , xn)–1) содержит её лишь тогда, когда
(x)( xn+1𝑓(x1, … , xn)–1) содержит её лишь тогда, когда 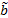 (x)≠0. Следовательно,
(x)≠0. Следовательно, 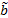 (x)=0 и мы можем записать наше равенство в виде
(x)=0 и мы можем записать наше равенство в виде
𝑓(x1, … , xn)N = ∑ 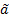 i(x1, … , xn) 𝑓i(x1, … , xn).
i(x1, … , xn) 𝑓i(x1, … , xn).
Это равенство и дает нам утверждение теоремы. ∎
Таким образом, для алгебраически замкнутого поля максимальные идеалы в кольце многочленов соответствуют точкам аффинного пространства, поскольку в доказательстве мы имели дело с алгебраическим подмножеством, а не с многообразием. Но утверждение теоремы Гильберта о нулях справедливо не только для точек аффинного пространства, но и, в целом, для любых аффинных многообразий. То есть если у нас имеется некоторое аффинное многообразие X⊂𝔸n над алгебраически замкнутым полем 𝕂, то любой максимальный идеал в кольце многочленов 𝕂[X] имеет вид идеала I(p) для некоторой точки p этого многообразия. Действительно, пусть A=𝕂[x1, … , xn] – кольцо многочленов, а 𝜑:A→𝕂[X] – естественная сюръекция и 𝔐⊂𝕂[X] – максимальный идеал. Тогда 𝜑-1𝔐⊂A – также максимальный идеал, т.к. отображение A∕𝜑-1𝔐⟶𝕂[X]∕𝔐 биективно. По следствию (14, Nss) имеем 𝜑-1𝔐=I(p). При этом идеал I(X)=Ker𝜑⊂𝜑-1𝔐=I(p) и, следовательно, точка p принадлежит многообразию X, т.е. p∈X. Поэтому, максимальные идеалы кольца регулярных функций находятся во взаимно однозначном соответствии с точками аффинного многообразия и это соответствие можно принять за определение точки аффинного многообразия.
Надо отметить, что на современном языке алгебраической геометрии, основанном на современном определении понятия схемы, в дополнении ко всему нами сказанному при доказательстве теоремы Гильберта о нулях, имеется ряд ещё очень содержательных и интересных фактов. Мы пока ограничимся на данном этапе классическими рассуждениями, предпринятыми выше, но в дальнейшем обязательно неоднократно вернемся к этому разделу алгебраической геометрии и уже с более современным её осмыслением. Самое важное, в чем мы пока должны были вполне убедиться, что каждый максимальный идеал в кольце регулярных функций QX является идеалом всех функций, зануляющихся в какой-то точке x∈X аффинного многообразия X. И если под максимальным спектром кольца Q понимать множество Spec𝔐Q его максимальных идеалов, то теорема Гильберта о нулях отождествляет Spec𝔐QX и аффинное многообразие X. А убирая нильпотенты в кольце, мы получаем, так называемую основную теорему алгебраической геометрии, говорящую нам о том, что если у нас имеется функтор R⟶Spec𝔐R из категории K конечно порожденных колец без нильпотентов в аффинные многообразия и функтор X⟶QX из категории аффинных многообразий в кольца регулярных функций на нем, то эти два функтора взаимно обратны и задают эквивалентность категорий аффинных многообразий Aff с категорией K * сопряженной к категории конечно порожденных колец без нильпотентов. С подробностями этих выводов, наиболее любопытно ознакомиться в, ставших уже легендарными, “листочках” – записях лекций М.С.Вербицкого по алгебраической геометрии.
Дата добавления: 2018-10-27; просмотров: 205; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
