Супералгебры и определение супермногообразия
Супермногообразия
И математика, ассоциированная с ними
Часть 1.
Построение супермногообразия
Общие замечания
Теория супермногообразий представляет собой результат переосмысления традиционных геометрических конструкций. Построение супермногообразия, как окольцованного пространства, позволяет считать его продуктом математики комплексов и производных категорий. Для определения окольцованного пространства нет никакой необходимости глубоко осмысливать и излагать предварительные идеи. Однако, это становится необходимым, когда возникает желание работать с супермногообразием, как объектом – в рамках тех или иных категорий. Многие классические вещи приходится переосмыслять и проводить довольно много подготовительной работы для каждого, часто совсем небольшого, шага при построении новых конструкций, где используется понятие супермногообразия. И это очень полезный опыт, поскольку крайне интересно наблюдать, как работают методы суперматематики в классических областях.
Здесь будет пространная вставка по следующему плану
· Суперматематика была открыта физиками – немного истории с некоторыми фактами (хотя бы упомянем понтификов из области суперструн и т.п.)
· Математики увидели, что можно сделать уже известными методами и стали разрабатывать новые подходы
· Во что все это превратилось у математиков…
|
|
|
· Во что все это превратилось у физиков… с замечанием, что ожидаемые суперсимметричные модели (хотя бы насчет суперсимметричных частиц-партнеров) пока ничем не подтверждены
· Математики тоже потихоньку начали склоняться к мысли, что данная область хоть и красива, но не слишком плодовита и в чем ее основные особенности. На каком то суперпримере – например, бегло ничего не доказывая, показать, что число автоморфизмов в супералгебрах больше, чем просто в их классических аналогах. И что это может дать, скажем, если сравнивать с автоморфизмами в теории Галуа или, если это не так, то, что в категории супермногообразий больше морфизмов, чем в категории векторных расслоений (у Лейтеса они есть явно выписанные т.н. свойство расщепимости)
Эта работа разделена на три небольших части. В первой части мы сделаем формальное построение супермногообразия, как окольцованного пространства. Таким образом, у нас возникнет некоторый объект, если рассматривать его в рамках теории категорий и функторов. Попытка подойти к построению супермногообразия, использующему другие математические конструкции, не только не дает ничего нового, но зачастую наталкивается на некоторые трудности, поэтому построение супермногообразия, именно как окольцованного пространства, видится наиболее удачной.
|
|
|
В виде дополнения к первой части приведена сводка основных определений из супералгебры. Следует отдать должное уважение к основателю алгебры и анализа с антикоммутирующими элементами – Ф.А.Березину, открывшему для нас основы этой теории в 80-х годах в виде целостного математического направления. Суперанализ, предложенный Ф.А.Березиным, обстоятельно раскрыт в его, переизданной недавно под редакцией Д.А.Лейтеса, работе “Введение в суперанализ”, а также в замечательных книгах, изданных на основе результатов семинара по суперсимметриям. Существует и скромная надежда на возможный популяризирующий результат данной работы и поэтому, наряду с довольно специализированными конструкциями, приведены построения, давно ставшие классическими и являющиеся исторической основой языка суперматематики.
Во второй части излагается структурная теория и классификация супермногообразия на основе пополнения суперсхем, причем как для аналитических, так и для дифференцируемых супермногообразий. Основные результаты, к которым мы обратимся во второй части, были хорошо известны еще в середине 90-х годов, поэтому обойтись без краткого их обзора не представляется возможным. Четкий план второй части не готов – впишу позже. Также коротко обсуждаются вопросы, имеющие отношение к теории супермногообразий, которые автор имел счастливую возможность обсудить с Ф.Ф.Вороновым в рамках спецкурса мехмата МГУ в начале 90-х годов.
|
|
|
В третьей части кратко излагаются некоторые вопросы из современной суперматематики, в том числе частично, и те, которые обсуждались в рамках семинара по суперсимметриям и которые издаются в настоящее время под редакцией Д.А.Лейтеса. Четкий план третьей части не готов – впишу позже.
Но абсолютно точно будут добавлены большие разделы, касающиеся Алгебр Клиффорда и Банаховых алгебр (некоммутативная теория Гельфанда-Наймарка) вплоть до разбора некоторых теорем.
В завершении приводится список литературы и комментарии.
Автор также благодарит своего научного руководителя Ю.Р.Мусина, работы которого по суперсимметричной механике, спинорам и супергравитации привлекли внимание к математике супермногообразий еще в то время, когда только начали появляться первые результаты, связанные с этой областью математики.
|
|
|
Важно отметить, что бурное развитие теории супермногообразий и суперматематики проходившее в 90-х годах постепенно угасало. Первоначально развитие было связанно с прикладными вопросами теоретической физики, исследованиями в области супергрупп калибровочных полей и математики суперструн. К сожалению, чисто математические работы, использующие понятие супермногообразия, уже к концу 90-х стали публиковаться довольно редко. Возможно, в это время шло продумывание дополнительных интересных разделов теории. И вот, к большой радости автора, мы снова наблюдаем возрождение интереса к этой красивой и содержательной области математики. Особенно приятно видеть этот ренессанс в рамках отечественной математической школы, где суперматематика и зародилась.
Неформальное построение
Скажем несколько слов об идеях, лежащих в основе построения супермногообразия. Стараясь избегать для начала необходимого формализма, предположим, что у нас имеется некоторое топологическое пространство M, обладающее рядом достаточно “хороших”, в смысле устройства его топологии, свойств, а {Ui⊂M│i 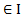 , (I – формальное множество индексов)} его покрытие, задающее топологию на М.
, (I – формальное множество индексов)} его покрытие, задающее топологию на М.
Задавая на M систему функций 𝑓i, отображающих каждое множество Ui в подобласть из пространства ℝn, причем так, чтобы на пересечениях Ui⋂Uj эти функции были согласованы в ℝn, мы получим содержательную часть построения многообразия через атлас с картами {Ui⊂M, 𝑓i:Ui→ℝn}. Аналитические свойства многообразия М определяются системой функций 𝑓i, а топологические свойства определяются топологией на M, и эти свойства согласованы. Так, если M – метрическое пространство, то открытыми будут ровно те его подмножества, которые открыты в смысле метрического пространства.
Обобщая, мы можем говорить о многообразии, как о паре (M, C(M)), где C(M) – система функций, определенная для каждого множества Ui из покрытия M. Для топологических пространств в качестве C(M) рассматривают алгебру непрерывных функций C0(M), а для бесконечно дифференцируемых многообразий – алгебру гладких функций C∞(M).
Переходя к определению супермногообразия, мы от обычных функций переходим к функциям со значениями в алгебре Грассмана 𝝠(q), вместо C(M) мы рассматриваем Q(M) – систему функций, локально утроенную как Q(U)=C(U)⊗𝝠(q), где U⊂M – множество из покрытия топологического пространства M. Каждая функция 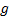 ∊Q(U) устроена как многочлен вида:
∊Q(U) устроена как многочлен вида:
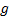 =
= 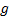 0(x) +
0(x) +  (x)
(x) 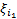 +
+ 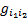 (x)
(x)  + … +
+ … +  (x)
(x)  ,
,
где x∊M, q – число образующих 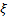 i алгебры Грассмана 𝝠(q). Определив так систему функций, мы должны позаботиться о хорошей согласованности её локальных частей на включениях и пересечениях множеств. Вполне естественно называть суперобластями локальные части Q(Ui)=C(Ui)⊗𝝠(q), обозначать которые мы будем Ui(n, q), где n – число образующих в M, а q – число образующих в алгебре Грассмана 𝝠(q). Также, естественно, мы поступим и с вложениями областей из покрытия M. Для каждого U⊂V мы будем полагать, что U(n,q) – ограничение функций V(n,q) с области V на U. Для согласования суперобластей на пересечениях мы конструируем функции, равные ограничению соответствующих функций из суперобластей на рассматриваемых нами пересечениях, причем ограничения должны совпадать на этих пересечениях.
i алгебры Грассмана 𝝠(q). Определив так систему функций, мы должны позаботиться о хорошей согласованности её локальных частей на включениях и пересечениях множеств. Вполне естественно называть суперобластями локальные части Q(Ui)=C(Ui)⊗𝝠(q), обозначать которые мы будем Ui(n, q), где n – число образующих в M, а q – число образующих в алгебре Грассмана 𝝠(q). Также, естественно, мы поступим и с вложениями областей из покрытия M. Для каждого U⊂V мы будем полагать, что U(n,q) – ограничение функций V(n,q) с области V на U. Для согласования суперобластей на пересечениях мы конструируем функции, равные ограничению соответствующих функций из суперобластей на рассматриваемых нами пересечениях, причем ограничения должны совпадать на этих пересечениях.
По сути, мы определяем некоторые глобальные функции, в точности повторяя построение классического пучка в алгебраической геометрии. В следующих разделах будут изложены основы построения пучка и смежных вопросов алгебраической геометрии и теории категорий, а пока отметим, что определить супермногообразие можно как пару (M, Q(M)), состоящую из топологического пространства M и пучка колец функций Q(M) на нем со значениями в алгебре Грассмана 𝝠(q). В такой формулировке наше построение имеет контравариантную природу. Мы определяем супермногообразие через систему функций, опуская при этом геометрическое содержание, поскольку классическая интерпретация такого содержания невозможна
Более того, можно сказать, что так мы реализуем фундаментальную идею дуальности функционально-геометрической (ковариантной) и функционально-алгебраической (контравариантной) точек зрения. Как оказывается, предъявить явно геометрический (ковариантный) эквивалент супермногообразия не представляется возможным, поскольку мы работаем в нашем построении не с классическими функциями и само понятие точки (как некоторого значения функции) утрачивает для нас привычный смысл. Все что остаётся для объяснения наших построений – это лишь сделать эквивалентный геометрическим построениям подход и дать соответствующие объяснения на языке теории категорий. Проводя построение супермногообразия, мы, на самом деле, строим объект некоторой дуальной (двойственной) категории, а геометрический эквивалент – это объект категории, которому соответствует наш первоначальный объект из двойственной категории. И это всё, что можно сказать о геометрической интерпретации ковариантного объекта, для нас представления об этом ковариантном объекте сводятся к признанию его формального наличия. Уже само определение понятия пучка, на языке теории категорий, проясняет его суть, как контравариантного функтора из категории топологических пространств в категорию колец функций. Поэтому и всё исследование, которое в классических построениях проводится в категории топологических пространств, для супермногообразия переходит в исследование области двойственной категории.
Построение пучка
| Предпучок, множество сечений, морфизм предпучков, пучок, росток, слой пучка, инициальная и финальная топология, индуктивный предел |
Начнем с определения предпучка. Пусть M – топологическое пространство. Предпучком А+ на топологическом пространстве M называется множество A+(U), определенное для каждого открытого множества U⊂M, вместе с морфизмом ограничений (сужений) ρ│  : A+(U)→A+(V) заданным для каждой пары множеств V⊂U из M, причем для каждого морфизма ограничений должны выполнятся следующие условия:
: A+(U)→A+(V) заданным для каждой пары множеств V⊂U из M, причем для каждого морфизма ограничений должны выполнятся следующие условия:
ρ│  = id, ρ│
= id, ρ│  ρ│
ρ│  = ρ│
= ρ│ 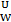 для любых множеств W⊂V⊂U из M.
для любых множеств W⊂V⊂U из M.
Множество A+(U) называется множеством сечений предпучка A+. В качестве A+(U) мы можем брать множества, снабженные дополнительной структурой кольца, модуля, алгебры и т.п. Так, задавая в A+(U) структуру кольца, мы будем иметь предпучок колец на M.
Дадим теперь определение морфизма для предпучков. Морфизмом предпучков 𝑓:A+→B+ на M называется набор отображений 𝑓(U):A+(U)→B+(U), по одному для каждого открытого множества U, причем каждое из отображений должно быть перестановочно с морфизмами ограничений ρ│  𝑓(U) = 𝑓(V) ρ│
𝑓(U) = 𝑓(V) ρ│  .
.
В качестве примера предпучка мы можем привести так называемый постоянный предпучок. Чтобы его построить возьмем в качестве G произвольную абелеву группу, тогда у нас имеется постоянный предпучок A+ с A+(U)=G для каждого U и с ρ│  = 1 для всех включений V⊂U из M.
= 1 для всех включений V⊂U из M.
Если мы сопоставим множеству U группу F=B+(U) всех функций из U в F с поточечным сложением функций в качестве групповой операции, а также определяя через ρ│  их естественные ограничения, то получим пример предпучка B+.
их естественные ограничения, то получим пример предпучка B+.
Если в качестве F=C+(U) выбрать группу вещественных чисел, то мы получим предпучок C+, для которого C+(U) будет определяться как группа всех непрерывных вещественнозначных функций на U.
Другими примерами являются предпучки гладких функций на гладком многообразии M, предпучки p-мерных дифференциальных форм на M, векторных полей на M и т.д.
Определить пучок – это наделить предпучок одним важным дополнительным свойством. Таким образом, пучок строится по предпучку и всегда, когда речь идет о пучке, следует помнить о таком порядке построения.
Пучком A называется предпучок A+ если для него дополнительно выполнено следующее условие: для любого покрытия U={Ui, i∈I} топологического пространства M и любого набора сечений si∊A(Ui) таких, что:
ρ│ 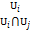 (si) = ρ│
(si) = ρ│ 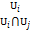 (sj),
(sj),
существует единственное сечение s∈A(U), такое, что si = ρ│  (s).
(s).
Морфизм пучков есть в точности морфизм соответствующих предпучков. Следует проявлять аккуратность в построении новых пучков. Иногда оказывается, что новый объект является лишь предпучком. В дальнейшем нам встретятся такие примеры.
По теории пучков издано много замечательных книг. Среди прочих, особо отметим обстоятельные монографии Г.Бредона и А.Гротендика (см. список литературы). Отметим, что понимание теории пучков для построения супермногообразий на практике сводится лишь к первоначальным определениям и некоторым простым свойствам пучка. Но теория пучков очень содержательна и красива. И, без сомнения, представляет большое практическое значение для построения основ теории супермногообразий.
Пусть у нас задан пучок A на топологическом пространстве M и точка x∊M. Часто случается, что вблизи точки x∊M пучок A имеет относительно простую локальную структуру. Для формального подхода к данной ситуации вводится понятие ростка. Определим росток sx сечения пучка A в точке x как класс эквивалентности пар (s,V), где y∊V и V – открытые окрестности, s∈A(V), по отношению эквивалентности (s,V) ~ (s',V'), где ~ обозначает существование множества W⊂V⋂V', причем
ρ│  (s) = ρ│
(s) = ρ│  (s').
(s').
Определим слой пучка A в точке x как множество Ax всех ростков в этой точке. Если воспользоваться языком индуктивных пределов, т.е. пределов направленного семейства однотипных множеств (в нашем случае – системе окрестностей, определение см. в конце данного параграфа), то слой есть индуктивный предел
Ax = ind lim U ∣ x∊U A(U).
Имея конструкцию слоя, мы можем понимать пучок в терминах расслоенного пространства. В общем виде, это есть тройка (E, M, π), где π – гомеоморфизм топологических пространств π:E→M. Пространство E (пространство предпучка A+) мы можем задать в виде дизъюнктного объединения E = 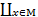 Ax.
Ax.
Для каждого s∊A(U) положим sx = ρ│  (s) и, затем, пусть E(s) = {sx, s∈U}⊂E.
(s) и, затем, пусть E(s) = {sx, s∈U}⊂E.
Множества E(s) образуют слабейшую топологию, где они выступают в качестве открытых множеств, π – гомеоморфизм, непрерывно отображающий E в M. В общем случае топология пучка нехаусдорфова.
Приведем здесь одно разъяснение, относящееся к определению пучка, весьма полезное для понимания. Если множество A+(U) – множество сечений предпучка A+, а si∈A+(Ui) какое либо его сечение, то si можно интуитивно представлять себе как функцию, определенную над Ui . Тогда условие морфизма ограничений ρ│ 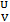 : A+(U) → A+(V), определенное как ρ│
: A+(U) → A+(V), определенное как ρ│  = id, вполне естественно, а условие ρ│
= id, вполне естественно, а условие ρ│  ρ│
ρ│ 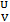 = ρ│
= ρ│  для любых W⊂V⊂U из M отражает транзитивность ограничения.
для любых W⊂V⊂U из M отражает транзитивность ограничения.
Когда мы вводим понятие пучка через предпучок, то есть добавляем условие, что для любого покрытия U={Ui, i∊I} топологического пространства M и любого набора сечений si∊A(Ui), подчиненного условиям ρ│ 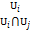 (si) = ρ│
(si) = ρ│ 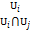 (sj), существует единственное сечение s∊A(U), такое, что si=ρ│
(sj), существует единственное сечение s∊A(U), такое, что si=ρ│  (s). Таким образом, мы строим в некотором смысле “аналитическое продолжение” предпучка на пространстве M. И наше дополнительное свойство, по которому мы определяем пучок, просто аксиоматизирует определение пучка по предпучку. Иначе говоря, из согласованных сечений на Ui можно склеить сечение над всем покрытием U={Ui, i∊I} топологического пространства M. И всякое сечение над U однозначно определяется набором своих ограничений на Ui.
(s). Таким образом, мы строим в некотором смысле “аналитическое продолжение” предпучка на пространстве M. И наше дополнительное свойство, по которому мы определяем пучок, просто аксиоматизирует определение пучка по предпучку. Иначе говоря, из согласованных сечений на Ui можно склеить сечение над всем покрытием U={Ui, i∊I} топологического пространства M. И всякое сечение над U однозначно определяется набором своих ограничений на Ui.
В определении пучка (абелевых групп на топологическом пространстве M) Г.Бредон использует пару (A, π), где A – топологическое пространство (вообще говоря, нехаусдорфово), а π: A → M – локальный гомеоморфизм, то есть так же, как мы делали выше, рассматривая пучок в терминах расслоенного пространства. При этом предполагается, что слой пучка в точке y (Ay = π-1 (y)) является абелевой группой и, что самое важное, групповые операции непрерывны.
Смысл последнего требования состоит в следующем. Обозначим через A∆A подпространство в A×A, состоящее из всех тех пар (α, β), для которых π(α)=π(β). Тогда отображение A∆A→A, переводящее (α, β) в α−β, должно быть непрерывно. Так пучок Q абелевых групп является пучком колец, если каждый слой снабжен структурой кольца и, в дополнении к требованию непрерывности групповых операций, отображение (α, β)→αβ из Q∆Q в Q должно быть непрерывно. А если мы желаем получить пучок колец с единицей, то помимо того требования, что всякий слой должен иметь единицу, нам необходимо потребовать (и это совсем не лишнее требование), чтобы и отображение, относящее каждой точке y∈M единицу кольца Qy, было непрерывным.
Выпишем теперь, в общем виде, условие, отвечающее за взаимно однозначное соответствие между пучками и предпучками. Это условие, проверка которого здесь опускается, состоит из двух частей.
Во-первых, требуется, чтобы для покрытия U={Ui, i∈I} топологического пространства M, где Ui открытое в M, и элементы s и t ∊ A(U) таковы, что s  =t
=t  для всех i∈I, то s=t
для всех i∈I, то s=t
Во-вторых, пусть {Ui} – семейство открытых подмножеств пространства M и U=  Ui. Если элементы si∈A(Ui) таковы, что si
Ui. Если элементы si∈A(Ui) таковы, что si  = sj
= sj  для всех i и j, то существует элемент s∈A(U) такой, что s
для всех i и j, то существует элемент s∈A(U) такой, что s  =si для каждого i.
=si для каждого i.
Эти два условия эквивалентны требованию точности последовательности (т.е. такой последовательности, в которой образ отображения Im𝑓 совпадает с ядром отображения Kerg):
𝑓 g
0 ⟶ A(U) ⟶  A(Ui) ⟶
A(Ui) ⟶  A(Uij),
A(Uij),
где Uij = Ui⋂Uj, 𝑓(s) =  s
s  и g(
и g(  si) =
si) =  ( si
( si  − sj
− sj  )
)
и где <i , j> обозначает упорядоченные пары.
Точность данной последовательности и есть то условие, которое устанавливает взаимно однозначное соответствие между пучками и предпучками. При выполнении данного условия предпучок будет являться пучком, и различать их нет необходимости.
Поскольку мы начали использовать различные топологические понятия, например такие, как индуктивный предел и слабейшая топология, нам нужно сделать небольшое отступление и сформулировать ряд определений и утверждений из топологии и теории множеств, которые нам понадобятся на протяжении всего изложения. Конечно, предполагается известным, что такое топология вообще, как она задается, а также начальные определения (такие, как база топологии, метрика, норма, мощность и подобные) и связанные с ними утверждения. Здесь мы кратко разберем лишь тот материал, который нам будет необходим, ни на какую полноту он претендовать не может.
Обсудим некоторые свойства на простом примере. Пусть у нас есть множество из двух элементов (точек) {1, 0}, на котором мы можем ввести четыре различные топологии 𝜏(k). Предварительно обозначив через X={0, 1}, а соответствующее топологическое пространство через Tk=(X, 𝜏(k)), k=1, …, 4, имеем для 𝜏(k):
𝜏(1)={∅, X}; 𝜏(2)={∅, X, {0}}; 𝜏(3)={∅, X, {1}}; 𝜏(4)={∅, X, {0}, {1}}.
Соответствующие базы для этих топологий запишем в виде:
𝔅(1)={∅, X}; 𝔅(2)={∅, X, {0}}; 𝔅(3)={∅, X, {1}}; 𝔅(4)={∅, {0}, {1}}.
В случаях 1-3 других баз выбрать нельзя, а четвертый случай допускает другую базу вида 𝔅(4)'={∅, {0}, {1}, X}. Таким образом, уже из этого простого примера мы можем сделать вывод, что база не должна обладать свойством минимальности и базу можно выбрать не единственным способом. Выпишем теперь все окрестности элементов 0 и 1 в каждом из пространств Tk.
(I) 𝜏0={X}, 𝜏1={X};
(II) 𝜏0={{0}, X}, 𝜏1={X};
(III) 𝜏0={X}, 𝜏1={X, {1}};
(IV) 𝜏0={{0}, X}, 𝜏1={X, {1}}.
Топологическое пространство называется хаусдорфовым (или отделимым), если две его различные точки имеют непересекающиеся окрестности. В нашем примере лишь пространство T4 отделимо. С другой стороны, всякое метрическое пространство отделимо, поэтому хаусдорфовость является необходимым условием метризуемости топологического пространства. Пространство T4 можно метризовать стандартным расстоянием 𝛿(0, 0)=0, 𝛿(1, 1)=0, 𝛿(0, 1)=1 и такая метрика порождает топологию 𝜏(4). Никакую топологию из оставшихся трех нельзя задать никакой метрикой, такой, чтобы она удовлетворяла всем аксиомам метрики.
Рассмотрим вещественный отрезок Y=[0; 1]. Объявим в нем открытыми пустое подмножество и всякое подмножество, получающееся из Y удалением конечного или счетного множества точек. Это определение топологии корректно, но полученное топологическое пространство TY не является хаусдорфовым. В самом деле, для любой произвольной точки x∈Y любая её окрестность Ox (непустая, ибо x∈OX) содержит все точки множества Y, кроме конечного или счетного числа. Но тогда любая окрестность Oy точки y тоже содержит все точки множества Y, кроме конечного или счетного их числа и, значит, не может целиком содержаться в Y\Ox. Следовательно, Ox⋂Oy≠∅, что и означает нехаусдорфовость пространства TY.
Теперь построим для примера пространства из двух точек список замкнутых множеств (замыкания являются дополнениями до открытого множества в данной топологии) для всех четырёх топологий 𝜏(k) и не забудем, что  =∅ ,
=∅ , 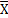 =X, получим:
=X, получим:
𝜎(1)={∅, X}; 𝜎(2)={∅, X, {1}}; 𝜎(3)={∅, X, {0}}; 𝜎(4)={∅, X, {0}, {1}}.
Сравнивая списки открытых и замкнутых множеств, мы можем заметить, что лишь пространство T4 является несвязным, поскольку только в нем есть открыто-замкнутые множества, отличные от ∅ и X, а отсутствие таких множеств суть наличие связности. Также можно отметить, что 𝜏(1) – слабейшая (кодискретная, антидискретная) топология, а 𝜏(4) – сильнейшая (дискретная). Топологии 𝜏(2) и 𝜏(3), не являясь слабейшей или сильнейшей, несравнимы между собой. Можно дать следующие определения. Пусть на множестве X заданы две топологии – 𝜏1 и 𝜏2. Тогда топология 𝜏1 слабее 𝜏2, если тождественное отображение (X, 𝜏2)→(X, 𝜏1) непрерывно. Соответственно, топология 𝜏2 сильнее топологии 𝜏1 и это равносильно тому, что 𝜏1⊂𝜏2. Чем слабее топология, тем больше сходящихся последовательностей, но меньше непрерывных функций и открытых множеств. На каждом множестве кодискретная топология является самой слабой, а дискретная – самой сильной. Если на множестве заданы некоторые топологии 𝜏1 и 𝜏2, такие, что 𝜏1 не слабее и не сильнее 𝜏2, то топологии 𝜏1 и 𝜏2 называются несравнимыми.
Пусть 𝑓:X→Y, где X – множество и Y – топологическое пространство. Если 𝜏 такая топология в X, что отображение 𝑓 непрерывно, то 𝑓 будет непрерывным отображением и для всякой топологии, которая сильнее топологии 𝜏 (иногда говорят – которая мажорирует топологию 𝜏). Таким образом, мы можем говорить, что топология 𝜏 является прообразом топологии на Y относительно отображения 𝑓. Этот прообраз состоит из всех множеств вида 𝑓-1(V), где V открыто в Y. Пусть 𝑓i:X→Yi, i∈I – семейство отображений, где X – множество, {Yi}i∈I – семейство топологических пространств. Тогда топология 𝜏 на X, такая, что для всякого топологического пространства Z отображение h:Z→X непрерывно тогда и только тогда, когда непрерывна композиция 𝑓i∘h для всякого i∈I, называется инициальной топологией на X относительно семейства отображений {𝑓i:X→Yi}i∈I.
Пусть 𝜏1 – инициальная топология на X относительно семейства отображений {𝑓i:X→Yi}i∈I. Если 𝜏2 – такая топология на X, что все отображения 𝑓i непрерывны, то топология 𝜏2 мажорирует топологию 𝜏1. Действительно, для двух соответствующих топологических пространств, заданных для одного множества X: (X, 𝜏1) и (X, 𝜏2) мы возьмем тождественное отображение idX:(X, 𝜏2)→(X, 𝜏1). Тогда все отображения 𝑓i∘idX=𝑓i непрерывны и, следовательно, само тождественное отображение idX непрерывно, что и означает, что 𝜏2 сильнее, чем топология 𝜏1. Из этого следует, что инициальная топология на X относительно семейства отображений единственна. Докажем, что она всегда существует. Пусть Ui=𝑓-1(Vi), где Vi открыто в Yi. Рассмотрим в X множество всех подмножеств вида  ⋂
⋂  ⋂…⋂
⋂…⋂  – это множество является базой некоторой топологии 𝜏 на X. Относительно данной топологии 𝜏 все отображения 𝑓i непрерывны, и значит, если h:Z→X непрерывное отображение, то и все композиции отображений 𝑓i∘h непрерывны.
– это множество является базой некоторой топологии 𝜏 на X. Относительно данной топологии 𝜏 все отображения 𝑓i непрерывны, и значит, если h:Z→X непрерывное отображение, то и все композиции отображений 𝑓i∘h непрерывны.
Пусть теперь непрерывны все композиции 𝑓i∘h:Z→ Yi, покажем, что в этом случае непрерывно отображение h. Для этого достаточно проверить непрерывность в случае, когда открытыми в X выступают базисные множества топологии 𝜏, тогда имеем:
h-1(  ⋂
⋂  ⋂…⋂
⋂…⋂  ) = h-1(
) = h-1(  )⋂h-1(
)⋂h-1(  )⋂…⋂h-1(
)⋂…⋂h-1(  ),
),
но композиции 𝑓i∘h непрерывны, поэтому обратное отображение
h-1(  ) = h-1((
) = h-1((  )-1(
)-1(  )) = (𝑓i∘h)-1(
)) = (𝑓i∘h)-1(  ), s=1, 2, …, k,
), s=1, 2, …, k,
открыто в Z, следовательно, и h-1(  )⋂h-1(
)⋂h-1(  )⋂…⋂h-1(
)⋂…⋂h-1(  ) – открыто в Z. Таким образом, h:Z→X – непрерывное отображение и топология 𝜏 на X – искомая инициальная топология относительно семейства отображений {𝑓i:X→Yi}i∈I. Кроме того, мы видим, что инициальная топология на X относительно семейства {𝑓i:X→Yi}i∈I является слабейшей топологией на X, относительно которой непрерывны все отображения 𝑓i:X→Yi.
) – открыто в Z. Таким образом, h:Z→X – непрерывное отображение и топология 𝜏 на X – искомая инициальная топология относительно семейства отображений {𝑓i:X→Yi}i∈I. Кроме того, мы видим, что инициальная топология на X относительно семейства {𝑓i:X→Yi}i∈I является слабейшей топологией на X, относительно которой непрерывны все отображения 𝑓i:X→Yi.
Важным примером инициальной топологии является произведение топологий. Пусть {Xi}i∈I – семейство топологических пространств и X=  Xi. Слабейшая топология на
Xi. Слабейшая топология на  Xi, относительно которой непрерывны все отображения-проекции X→Xi, называется произведением топологий пространств Xi.
Xi, относительно которой непрерывны все отображения-проекции X→Xi, называется произведением топологий пространств Xi.
Инициальная топология является также примером проективного предела на соответствующем множестве-носителе в категории топологических пространств Top и мы обсудим это в § 2.4.
Теперь изменим направление отображений в нашем семействе и получим сопряженное для инициальной топологии определение. Пусть {𝑓i:Yi→X}i∈I – семейство отображений, где X – множество, а {Yi}i∈I – семейство топологических пространств. Топология 𝜏 на X, такая, что для всякого топологического пространства Z отображение h:X→Z непрерывно тогда и только тогда, когда непрерывны все композиции отображений h∘𝑓i:Yi→Z называется финальной топологией на X относительно семейства отображений {𝑓i:Yi→X}i∈I.
Обратно к тому, как это утверждалось для инициальной топологии, мы можем теперь утверждать, что если 𝜏1 – финальная топология на X относительно семейства {𝑓i:Yi→X}i∈I и если 𝜏2 – такая топология на X, что все отображения 𝑓i:Yi→X непрерывны, то топология 𝜏1 мажорирует топологию 𝜏2. Относительно семейства {𝑓i:Yi→X}i∈I отображений, финальная топология на множестве X единственная, докажем её существование. Для этого рассмотрим множество всех подмножеств V в X таких, что 𝑓i-1(V) открыто в Yi для всякого i. Множество таких подмножеств в X является некоторой топологией 𝜏 на X, в которой все отображения 𝑓i непрерывны. И, поэтому, если h – непрерывно, то и все композиции h∘𝑓i непрерывны.
Пусть теперь все композиции h∘𝑓i:Yi→Z непрерывны, тогда отображение h непрерывно. Действительно, если U открытое подмножество в Z, то h-1(U)=V и 𝑓i-1(V)=𝑓i-1(h-1(U))=(h∘𝑓i)-1(U) открыто в Yi, что означает, что подмножество V открыто в топологии 𝜏 на X. Таким образом, топология 𝜏 на X является искомой финальной топологией относительно семейства отображений {𝑓i:Yi→X}i∈I. Кроме того, мы можем видеть, что финальная топология на X относительно семейства отображений {𝑓i:Yi→X}i∈I является сильнейшей топологией на X, относительно которой непрерывны все отображения 𝑓i:Yi→X.
Важным примером финальной топологии является фактортопология. Пусть X – топологическое пространство и на X (как на множестве) задано отношение эквивалентности 𝔎 (поэлементно обозначаемое ∼), порождающее фактормножество X∕𝔎 и естественную проекцию 𝜋:X→X∕𝔎 для него. Сильнейшая топология на X∕𝔎, при которой непрерывна проекция 𝜋, называется фактортопологией топологии пространства X, а проекция называется факторотображением.
Приведем два примера. Пусть имеется подпространство U⊂X, а отношение эквивалентности 𝔎 на X задано так: x1∼x2 тогда и только тогда, когда либо x1=x2, либо x1∈U и x2∈U. Факторпространство X∕𝔎 обозначается X∕U и говорят, что X∕U получается из X стягиванием U в точку. В данном примере нужно отметить, что если U само является точкой U=pt, то X∕pt гомеоморфно X (т.е. имеется взаимно однозначное и взаимно непрерывное отображение топологических пространств X и X∕pt), а X∕∅ гомеоморфно несвязному объединению X и точки.
Для второго примера будем говорить, что группа G действует слева на пространстве X, если для каждого элемента g∈G задано непрерывное отображение 𝛼g:X→X, такое, что 𝛼e=id и 𝛼gh=𝛼g∘𝛼h. Каждое отображение 𝛼g является гомеоморфизмом с обратным отображением 𝛼g - 1. Точку 𝛼g(x) обозначим gx. Орбитой точки x∈X под действием группы G называется подмножество Gx={gx│g∈G}. Орбиты разных точек не пересекаются или совпадают и, следовательно, задают отношение эквивалентности 𝔎 на X следующим образом: x∼y если существует такой g∈G, что gx=y. В результате мы получаем соответствующее факторпространство X∕𝔎, которое называется пространством орбит по действию группы G и которое обозначается X∕G.
Финальная топология является также индуктивным (другое название – прямым) пределом на соответствующем множестве-носителе в категории топологических пространств Top (когда множество-носитель наделяется финальной топологией). Сейчас мы дадим определение индуктивного предела для множеств, а его определение на языке теории категорий разберем в следующем параграфе. Поскольку понятие индуктивного предела у нас появляется при введении понятия слоя пучка, то определим его для объектов – множеств с алгебраической структурой, которые участвуют в построении соответствующих пучков. Пусть это будут любые однотипные алгебраические объекты, такие как алгебры, кольца, модули над некоторым произвольным кольцом и т.д. Чтобы получить индуктивный предел, необходимо построить последовательность таких однотипных алгебраических объектов, индексированную некоторым направленным множеством.
Более строго, пусть у нас есть некоторое направленное множество I с отношением предпорядка ≼, т.е. бинарного отношения обладающего свойством рефлексивности ∀ i∈I : i≼i и транзитивности ∀ i,j,k∈I : (i≼j⋀j≼k) ⇒ (i≼k). Отметим, что свойство антисимметричности, записываемое как ∀ i,j∈I : (i≼j⋀j≼i) ⇒ i=j, и превращающее множество I в множество нестрого частичного порядка, здесь не требуется. Пусть каждому элементу i∈I сопоставлен алгебраический объект Xi, и каждой паре (i, j), i,j∈I, для которой i≼j, поставлен в соответствие гомоморфизм 𝑓ij:Xi→Xj, такой что 𝑓ii – тождественное отображение на Xi для любого i∈I и 𝑓ik=𝑓jk∘𝑓ij для любых i≼j≼k∈I. Такую систему объектов и гомоморфизмов назовем направленной системой (Xi, 𝑓ij). Тогда множество-носитель X индуктивного предела направленной системы (Xi, 𝑓ij) определяется как фактормножество дизъюнктного объединения множеств-носителей Xi по отношению эквивалентности 𝔎:
X = ind lim Xi =  Xi∕𝔎.
Xi∕𝔎.
Отношение эквивалентности ∼ вводится следующим образом – два элемента xi∈Xi и xj∈Xj эквивалентны (xi∼xi), если существует такое k∈I, что 𝑓ik(xi)=𝑓jk(xj).
Это интуитивно означает, что два элемента нашего дизъюнктного объединения эквиваленты тогда и только тогда, когда они, начиная с некоторого k станут эквивалентными в направленной системе (Xi, 𝑓ij). Можно дать определение введенной эквивалентности через понятие транзитивного замыкания. Для этого вспомним, что транзитивное замыкание – это операция на бинарных отношениях, а именно – транзитивное замыкание бинарного отношения 𝔎 (в нашем случае отношение 𝔎 состоит в том, что каждый элемент эквивалентен своим образам, т.е. xi∼𝑓ik(xi)) на множестве M есть наименьшее транзитивное отношение на множестве M, включающее отношение 𝔎. Согласно такому пониманию введенной эквивалентности, а также имея канонические морфизмы 𝜙i:Xi→X, отправляющие каждый элемент xi в его класс эквивалентности, мы можем получить добавленную алгебраическую структуру на X. Если у нас имеется произвольное семейство подмножеств некоторого множества, то предпорядок на такой структуре можно задать по включению. Если данный предпорядок будет направленным, то индуктивный предел будет являться обычным объединением множеств.
Пусть теперь у нас задан некоторый пучок A(M) на топологическом пространстве M. Для некоторой точки x∈M её открытые окрестности U образуют направленную систему по включению вида U≼V, если V⊂U. Функтор пучка (см. определение функтора в след. §) сопоставляет этой направленной системе соответствующую направленную систему (A(U), ρ│  ), где ρ│
), где ρ│  морфизм сужений. Тогда слой пучка A(M) в точке x можно определить как индуктивный предел Ax= ind lim U ∣ x∊U A(U) в полном соответствии с уже имеющимся определением.
морфизм сужений. Тогда слой пучка A(M) в точке x можно определить как индуктивный предел Ax= ind lim U ∣ x∊U A(U) в полном соответствии с уже имеющимся определением.
Категории и функторы
Категорией L мы будем называть пару (ObL, MorL), где ObL – некоторый класс объектов, а MorL – набор множеств Hom(A, B) по одному на каждую пару A, B∈ObL.
Элементы из Hom(A, B) называются морфизмами φ: A → B.
В MorL также задан закон композиции, т.е. набор отображений
Hom(A, B) ⨯ Hom(B, C) → Hom(A, C)
В качестве аксиом мы принимаем следующие положения:
1. По каждому морфизму φ однозначно определяются такие A и B из ObL (A, B∈ObL), что φ∈Hom(A, B). Иными словами, множества попарно не пересекаются.
2. Для каждого объекта A∊ObL существует тождественный морфизм, обозначаемый idA:A→A и однозначно определяемый тем свойством, что idA∘ψ=ψ, idA∘φ= φ всякий раз когда эти композиции определены.
3. Композиция морфизмов ассоциативна
(χ∘ψ)∘φ = χ∘(ψ∘φ) для любых φ: A→B, ψ: B→C, χ: C→D.
Более распространенным в настоящее время является другое определение категории, а именно категория L –это множество объектов ObL, причем каждой паре объектов A, B∈ObL сопоставлено множество морфизмов между ними Hom(A,B), и, причем каждому объекту A∈ObL сопоставлен выделенный тождественный морфизм idA∈Hom(A,A). На множестве морфизмов также определена операция композиции, т.е. для любой тройки A, B, C ∈ ObL определено отображение
∘ : Hom(B, C) × Hom(A, B) → Hom(A, C),
удовлетворяющее следующим тождествам:
χ ∘ (ψ ∘ φ) = (χ ∘ ψ) ∘ φ,
φ ∘ idA = idB ∘ φ, φ: A → B,
при условии, что все указанные операции в них определены, и что, в свою очередь, выражается через коммутативную диаграмму,
B
φ ψ
A  C
C
где для любой последовательности стрелок φ и ψ определена единственная стрелка ψ∘φ, которая делает данную диаграмму коммутативной.
Условия существования единицы и ассоциативности означают коммутативность следующих диаграмм:
| idA A A φ φ φ B B idB | B C A D |
При использовании языка коммутативных диаграмм, нам необходимо иметь в виду, что диаграмма не является математическим объектом, а только лишь рисунком для облегчения чтения. Поэтому будем принимать относительно диаграмм соглашения, принятые в теории множеств и алгебраической аксиоматике, принятой в работах группы Бурбаки. Чтобы не углубляться в данную аксиоматику, мы опустим ряд деталей. Будем называть диаграмму коммутативной, если результат композиции морфизмов не зависит от пути, который проходит из вершины в вершину диаграммы вдоль стрелок.
Приведем примеры категорий. Для их определения нам необходимо задать структуру в объектах множеств из данной категории и отображения между множествами, согласованные с заданной структурой.
Set – категория множества, объектами которой являются множества, а морфизмы MorSet – это множества Hom(A, B)={все функции из А в B}, понятно, что нулевые морфизмы – это пустые функции ∅ → X.
Diff – категория бесконечно дифференцируемых многообразий и гладких отображений между ними;
Ab – категория абелевых групп и их гомоморфизмов;
A-mod – категория левых модулей над фиксированным кольцом A и их гомоморфизмов;
Top – категория топологических пространств и непрерывных отображений между ними;
TopX – категория топологического пространства X, где объекты ObTopX={открытые подмножества X}, а морфизмы MorTopX – это множества Hom(U,V) = {естественное вложение U→V, если U⊂V и ∅, если U⊄V}.
Заметим, что TopX является частным случаем более абстрактной категории частично упорядоченных множеств P. Если у нас имеется частично упорядоченное множество (P, ⩽), то объектами будут сами множества ObP=P, а Hom(A, B) равен одноэлементному множеству {*} при A⩽B и ∅ в противном случае. Утверждение о существовании композиции морфизмов – суть утверждение о транзитивности ⩽.
Также любопытен пример так называемой дискретной категории, в которой множеством объектов является некоторое произвольное множество S (=ObS), а множество морфизмов тривиально, т.е. Hom(A, B) = ∅ , если A≠B и Hom(A,A)={idA}.
Мы можем привести примеры категорий из физики. Таким примером является категория диаграмм Фейнмана, где объектами являются всевозможные наборы частиц в некотором состоянии. А морфизмы между двумя состояниями – это диаграммы, соответствующие переходу из первого состояния во второе. Можно обобщить этот пример на случай любой динамической системы и рассматривать категорию, где объектами будут состояния этой системы, а морфизмами – процессы, переводящие систему из одного состояния в другое. Если в качестве морфизмов рассмотреть алгоритмы, которые переводят заданные данные на входе в заданные данные на выходе, то мы получим еще один пример – категорию алгоритмов.
Еще одна интересная категория, называемая гомотопической категорией HoTop, возникает, если в качестве объектов рассмотреть CW-комплексы. CW-комплексы – это топологические пространства, разбитые на n-мерные клетки, каждая из которых гомеоморфна n-мерному шару и удовлетворяет некоторым дополнительным свойствам, приспособленным для нужд теории гомотопий. Первоначально такие комплексы были введены Д.Уайтхедом, буквы C и W происходят от двух условий, наложенных на клетки – closure-finiteness и weak topology, а именно, (С) граница каждой клетки содержится в объединении конечного числа клеток меньших размерностей и (W) подмножество пространства X замкнуто тогда и только тогда, когда замкнуто его пересечение с замыканием каждой клетки. Морфизмами в гомотопической категории являются классы гомотопных отображений между CW-комплексами. Отношение гомотопности согласовано с композицией непрерывных отображений, поэтому можно определить композицию морфизмов в HoTop, как гомотопический класс композиции соответствующих морфизмов в категории Top. Множество морфизмов в гомотопической категории обычно обозначается через π(X,Y). Важность этой категории вытекает, например, из того, что множество морфизмов из одноточечного пространства в Х, в наших обозначениях – π(*,X), суть множество компонент линейной связности комплекса X, а множество π(S1,X) – его фундаментальная группа, где S1 – одномерная сфера.
Понятно, что один и тот же объект может быть отнесен к разным категориям. Все зависит от того, какая характеристика из структуры объекта нас интересует. Например, свойство хаусдорфовости помещает топологическое пространство в подкатегорию хаусдорфовых пространств, но это же пространство остается и объектом более общей категории Top и, одновременно, еще более общей категории Set при описании топологического пространства, как простого множества. Поэтому нам важно определить способ перехода от одной категории к другой. Такие морфизмы между категориями называются функторами. Начнем с определения ковариантного функтора.
Функтором F из категории K со значениями в категории Ḱ назовем соответствие
F : K → Ḱ = (ObK → ObḰ, MorK → Mor Ḱ),
такое что A∊ObK → F(A)∊Ob Ḱ, φ∊Hom(A, B) → F(φ) ∊Hom(F(A), F(B)),
причем F(φψ)=F(φ)F(ψ) для всех φ,ψ∊MorK для которых φψ определен.
Соответственно, для тождественных отображений F(idA)=idF(A).
Как видно из определения, функтор отображает категории таким образом, чтобы их структура сохранялась. Как правило, определение функтора обычно делается через контравариантный функтор, что довольно удобно и более наглядно. Но мы предпочли начать с ковариантного определение функтора и теперь, исходя из него, сделаем построение контравариантного.
Для нас наиболее важным примером функтора оказывается функтор из категории TopX топологического пространства X в категорию множеств Set, возможно снабженных дополнительной структурой колец, модулей, алгебр и других, то есть функтор
ℱ : TopX → Set категория множеств (алгебр, модулей, колец…)
Используя данный функтор можно ввести совсем короткое и красивое определение предпучка, как контравариантного функтора из категории TopX в категорию множеств Set. Чтобы дать определение контравариантного функтора, нам потребуется определение двойственной (или дуальной) категории, которая строится с использованием теоретико-категорного принципа двойственности, который состоит в том, что для любого утверждения теории категорий можно сформулировать двойственное утверждение с помощью обращения стрелок, при этом истинность утверждения не изменится. Двойственный понятия обычно получают приставку ко-, например произведение и копроизведение пары объектов
Пусть нам дана некоторая категория K. Определим двойственную категорию K ° как категорию (ObK °, MorK °), где ObK ° = ObK, то есть те же самые объекты, что и объекты категории K. А морфизмы MorK ° мы определим как множества морфизмов HomK °(A, B)=HomK(B, A), где композиция φψ в категории K ° определяется как ψφ в категории K. Такую запись определения морфизмов для двойственной категории и называют иногда обращением стрелок. Объекты категорий K ° и K - это те же самые объекты, но желая подчеркнуть принадлежность объекта A к двойственной категории K °, мы будем обозначать его символом А°, а соответствующий морфизм φ∊HomK(B,A) символом φ°∊HomK °(A, B). Понятно, что φ°ψ°=(ψφ)°, взятые в соответствующих категориях.
Иногда говорят о контравариантном функторе F °, как о соответствии, для которого в паре соответствий F ° : K → Ḱ = (ObK → ObḰ, MorK → MorḰ) для φ:A→B, A,B∊ObK, выполнено F °(φ): φ(B) → φ(A) и F °(φψ) = F °(ψ)F °(φ).
В терминах нашей дуализации мы определим контравариантный функтор F : K → Ḱ, как тождественно согласованный ковариантный функтор G из двойственной категории K ° в категорию Ḱ. Приведем здесь рисунок, который проясняет, как именно согласованы функторы F и G.
| Категория K Объекты A, B, … Морфизмы Hom(A, B) | дуализация | Двойственная категория K ° Объекты A°=A, B°=B,… Морфизмы HomK°(A, B)=HomK(B, A) |
| F контравариантный функтор | G ковариантный функтор | G |
| Категория Ḱ Объекты F(A)=A, F(B)=B… Морфизмы HomḰ(F(B),F(A))=HomK°(A, B) | эквивалентность | Категория Ḱ Объекты G(A)=F(A)=A,… Морфизмы HomḰ(G(B°),G(A°))= HomḰ(F(B),F(A))=HomK°(A, B) |
Из этого рисунка понятно, что новая категория Ḱ, полученная через контравариантный функтор F полностью эквивалента введению двойственной категории, а двойное применение к категории принципа двойственности переводит категорию в себя.
Помимо предпучка, как примера контравариантного функтора, можно привести большой класс функторов, которые получаются, если упрощается структура объекта исходной категории. По этой причине их еще называют функторами забвения. Так функтор из категории Diff бесконечно дифференцируемых многообразий и гладких отображений между ними в категорию Top топологических пространств и непрерывных отображений между ними будет одним из примеров функтора забвения.
Казалось бы, на определении понятия функтора, как соответствия между двумя категориями и должно заканчиваться обобщение в рассмотрении естественных математических конструкций. Но оказывается, что и сами функторы могут стать объектами категории, если ввести понятие морфизма функторов.
Если у нас имеется два функтора F и G из категории K в категорию Ḱ, то функторный морфизм ƒ: F → G определим как семейство морфизмов
ƒ (X) : F(X) → G(X)
по одному для каждого объекта X ∊ ObK, которое для всякого морфизма φ: X→Y в категории K делает коммутативной диаграмму
F(X)  G(X)
G(X)
F(φ) G(φ)
F(Y)  G(Y)
G(Y)
Можно определить как тождественный функторный морфизм, так и композицию функторных морфизмов, после чего функторы K → Ḱ можно рассматривать как объекты категории функторов Funct(K , Ḱ), построенной для заданных категорий K и Ḱ.
Есть еще один вопрос, относящийся к определению категории, где объекты и морфизмы по определению образуют множества, а именно вопрос, касающийся категории всех множеств. При рассмотрении такого общего случая определение категории уже некорректно. Обычно этот вопрос опускают, но мы его немного проясним. Ситуация разрешается при помощи аксиомы универсума Гротендика. Для этого мы предположим существование универсумов 𝔘 – моделей теории множеств – бесконечного класса достаточно больших бесконечных множеств таких, что произведение множеств универсума 𝔘, а также подмножество или множество подмножеств любых множеств универсума лежало в 𝔘. Более того, в универсуме должно лежать множество ℕ натуральных чисел и для любых элементов u, v ∊ 𝔘 из универсума 𝔘 множество {u, v} ∊ 𝔘.
Аксиома универсума Гротендика утверждает, что универсумы существуют, причем для любого универсума 𝔘 существует универсум 𝔙, такой, что 𝔘∊𝔙. Эта аксиома совместима с аксиоматикой теории множеств и для того, чтобы избежать проблем, связанных с аксиоматикой в дальнейшем, мы будем предполагать фиксированным некоторый универсум 𝔘. Множества, лежащие в 𝔘, называются малыми, а все остальные множества – большими. Так простейший модельный пример из уже приведенных – это категория множеств Set и по введенной аксиоматике – это большая категория.
Геометрические категории
Взглянем теперь на классическую конструкцию многообразий с точки зрения понятий пучка и категории. Многообразие некоторого класса – это пара (M,Q(M)), которая состоит из M – хаусдорфова топологического пространства со счетной базой и пучка Q(M) на M. Описать некоторый класс многообразий для нас означает – описать в некотором смысле локальную модель этого класса. Тогда пара (M,Q(M)) будет принадлежать к описываемому классу, если для каждой точки x∊M существует окрестность U, для которой естественное ограничение пары (M,Q(M)) на U, представленное в виде пары (U,Q(M)ǀU) локально изоморфно нашей модели. Именно для этого нам необходимо будет ввести понятие модельной категории. Если пока не обращаться к строгому определению модельной категории, а рассматривать классические определения отталкиваясь от их локальной модели, то можно дать определение локальных моделей двух классов многообразий – топологических C0 и бесконечно дифференцируемых С∞ – следующим образом.
Функции 𝑓, которые будут присутствовать в локальной части пучка, мы будем называть частичными, имея в виду пару (D(𝑓), 𝑓), где D(𝑓)⊂U – открытое подмножество, а 𝑓: D(𝑓) → ℝ – функция на нем. Тогда можно сказать, что:
(I) локальная модель класса С0 – это пара (область U⊂ℝn, непрерывные частичные функции в U с вещественными значениями)
(II) локальная модель класса С∞ – это пара (область U⊂ℝn, бесконечно дифференцируемые частичные функции в U с вещественными значениями).
Иногда встречается аксиоматика задания дифференцируемого многообразия, в которой о свойствах основного пространстве M ничего не известно, т.е. изначально его задают как множество. Открытыми множествами при такой аксиоматике становятся прообразы отображений из множеств в открытые множества ℝn. Топология на множестве М задается в виде системы открытых прообразов отображений 𝑓i:Ui⊂M→Vi⊂ℝn и их объединений. И хотя этот метод и порождает нам пару, состоящую из пространства и системы функций на нем вида (М,{𝑓i}) мы сознательно откажемся от логики данной аксиоматики, и будем использовать понятие пучка. Аксиоматика, при которой об основном пространстве, для которого делаются дальнейшие построения, первоначально ничего не известно, используется обычно для подготовки определения многообразия к введению векторных полей на нем и дальнейшему переходу к формализму квантовой механики, введению операторов, тензорного аппарата и т.п. Но, при таком подходе, и само векторное поле, с операцией внешнего произведения векторов, должно быть в некотором смысле аксиоматически пополнено. Уместно считать, что выполняются некоторые ограничения – в минимальных требованиях, это свойства сепарабельности и предгильбертовости. Сепарабельное пространство – это пространство, содержащее счетное всюду плотное множество (для классической аксиоматики понимаемое “в индуцированной топологии”, что уже само по себе порождает некоторую специфику в полагании данного свойства). Это свойство в классической аксиоматике требуется для конструктивности построений, например, чтобы образы непрерывных отображений были также сепарабельны. Свойство предгильбертовости означает, что в пространстве введена метрика, хотя само пространство, возможно, и не полное относительно этой метрики (не банахово). Впрочем, практически все предгильбертовы пространства можно пополнить и это свойство дает нам возможность введения и работы с линейными операторами. Иначе, когда свойства заранее не обговорены, авторы классического подхода вынуждены прибегать к требованию свойства “неособенности”, например, требованиям ненулевого якобиана для функций на пересечениях областей множеств, но уже с индуцированной топологией, что, конечно, не поддается очевидному обобщению.
В данной работе основное пространство будет всегда заранее наделено топологией и необходимыми свойствами типа гладкости. Мы всегда будем отталкиваться именно от топологического пространства, а не от множества с индуцированной топологией, что важно, когда применяются термины теории категорий. Также мы не уточняем вопросов, касающихся связности пространства М, предполагая в дальнейшем, что наше основное (подстилающее) пространство (многообразие) хаусдорфово и связно, если противное не оговорено явно.
Пучок Q(M) многообразия (M,Q(M)) называется структурным. Выделение данного вида пучка оправдывается тем, что наша дальнейшая цель – перейти к категории окольцованных пространств, в которой сечения пучка уже не будут являться функциями. Но поскольку мы еще не ввели определение окольцованного пространства, немного отложим прояснение данного вопроса и посмотрим, как согласуются описанные выше примеры локальных моделей с классическими определениями многообразия соответствующего класса через карту и атлас.
Атласом пространства M называется набор множеств {Ui⊂M}, образующих покрытие с выбранной для каждого множества системой координат (x 1i,…,x ni), таких, что отображение 𝑓 : Ui → ℝm является открытым вложением, а на пересечениях Ui⋂Uj координаты xi являются непрерывными (для С0) или гладкими (для С∞) функциями от xj. По атласу φ∊Q(U) строится пучок: сечения являются таковыми, если на всех непустых пересечениях U⋂Ui функция φ является непрерывной (или гладкой). В свою очередь, по пучку строится атлас. Для этого мы возьмем локальные модели для соответствующего класса (U,Q(U)) и покрытие {Ui} пространства M. Эти локальные модели порождают атлас, где в качестве набора множеств мы возьмем множество всех пересечений {U⋂Ui}.
Мы можем превратить С0 и С∞ в категории, для этого нам надо определить морфизмы Φ: (M,Q(M)) → (N,Q(N)), где наши пары – многообразия соответствующего класса. Но поскольку мы работаем лишь в рамках локальной модели выбранного класса, нам потребуется использовать структурный пучок. Для непрерывных и гладких (и даже аналитических) многообразий все морфизмы Φ вполне естественно определяются по непрерывным отображениям φ: M → N. Мы также должны учесть, что локальные координаты на Vi⊂N выражаются через локальные координаты на Ui⊂M в виде функций выбранного класса. По отображению φ мы строим перенос сечения 𝑓∊QN(V) на сечение g(𝑓)∊QM(φ-1(V)) полагая, что g(𝑓)(x)= 𝑓(φ(x)). Таким образом, Φ является морфизмом тогда и только тогда, когда g(𝑓)∊QM(φ-1(V)). Множество отображений {Φ} образует нам класс морфизмов соответствующей категории, для которых все категорные аксиомы определяющие морфизмы выполнены.
Теперь нам потребуется ввести определение алгебры Грассмана. Если брать за определение алгебру над некоторым полем ℙ, то можно кратко определить алгебру – как векторное пространство, снабженное билинейным умножением. Т.е. алгебра над полем – это одновременно векторное пространство и кольцо, для элементов которого структуры векторного пространства и кольца являются согласованными. Обобщением алгебры над полем является алгебра над кольцом, но мы пока ограничимся случаем алгебры над полем ℙ (с характеристикой charℙ≠2).
Пусть V – конечномерное векторное пространство размерности d над полем ℙ. Грассманова алгебра (или алгебра Грассмана) над V – это такое множество 𝝠(q), что выполнены следующие условия:
(I) 𝝠(q) – ассоциативная алгебра с единицей e над ℙ;
(II) V ⊂ 𝝠(q);
(III) для любого v ∈ V выполнено v2=0;
(IV) 𝝠(q) имеет размерность 2d;
(V) 𝝠(q) порождается единицей e и пространством V.
Понятно, что e∉V, т.к. e2=e≠0, но при этом из (III) v2=0 для любых v∈V. Свойство (V) говорит нам о том, что всякий элемент из 𝝠(q) есть сумма произведений скалярных кратных (в рамках нашего поля) единицы e и элементов векторного пространства V. Из свойства (III) также следует, что для любых u, v ∈V, uv = -vu, поскольку 0=(u+v)2=u2+uv+vu+v2.
Особый интерес представляет условие (IV). Суть данного условия состоит в том, что среди элементов 𝝠(q)нет других соотношений, кроме тех, которые вытекают из условия (III). Для любого базиса e1,…, ed пространства V существует некоторый базис пространства 𝝠(q) и элементы базиса в 𝝠(q)находятся во взаимно однозначном соответствии с подмножествами {1,…,d}. Причем пустому подмножеству ∅ соответствует элемент e∅=e, а подмножеству s={i1,…,iq}, где i1<…< iq, соответствует элемент ξs=ei1…eiq. Всего таких подмножеств имеется 2d и элементы ξs образуют базис пространства 𝝠(q). Это следует из того, что в силу свойства (V) для всякого ξ∈𝝠(q) имеем
ξ = a0e∅ + 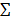 (произведения элементов V) =
(произведения элементов V) =
= a0e∅ + 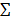 (коэффициенты из поля ℙ) · (произведения элементов ei из V).
(коэффициенты из поля ℙ) · (произведения элементов ei из V).
Поскольку элементы из V антикоммутативны, то, следовательно, мы можем в любом произведении расположить сомножители ei по возрастанию их индексов и получим, что все слагаемые, кроме es, будут равны нулю из чего и следует, что ξs порождают𝝠(q). Поэтому мы в дальнейшем будем пользоваться не совсем полным, но достаточным для наших задач, определением, где под алгеброй Грассмана 𝝠(q) мы просто будем рассматривать алгебру, порожденную системой образующих ξ1,…, ξq с определяющими соотношениями ξi2=0 и ξi ξj + ξj ξi = 0 для любых i,j∈{1,…,q}.
Элемент ξ∈𝝠(q) мы будем называть однородным степени p если он может быть записан как сумма произведений по p элементов из V, т.е. в виде суммы

Где as∈ℙ, а P – совокупность всех подмножеств {1,…,d}, имеющих ровно p элементов. Совокупность таких однородных степени p элементов ξ∈𝝠(q) образует линейное подпространство 𝝠p(q) алгебры 𝝠(q) размерности  . Причем 𝝠p(q)𝝠r(q)⊂𝝠p+r(q) и если ξ∈𝝠p(q) η∈𝝠r(q), то ξη=(-1)prηξ в силу антикоммутативности, что указывает на то, что алгебра Грассмана градуирована.
. Причем 𝝠p(q)𝝠r(q)⊂𝝠p+r(q) и если ξ∈𝝠p(q) η∈𝝠r(q), то ξη=(-1)prηξ в силу антикоммутативности, что указывает на то, что алгебра Грассмана градуирована.
Алгебру Грассмана иногда называют также внешней алгеброй на соответствующем векторном пространстве. Эта терминология происходит от того, что, задавая операцию внешнего произведения, мы получаем алгебру Грассмана для данного векторного пространства, которая позволяет описывать устройство его подпространств и которая не зависит от выбора базиса в векторном пространстве.
Алгебра Грассмана – достаточно естественная алгебраическая система. Так, например, если рассмотреть классическое понятие дифференциальной формы, то для некоторой координатной системы в выбранной точке мы можем представить дифференциальную форму в виде выражения вида ∑ai1…ipdxi1…dxip, где суммирование идет по всем упорядоченным подсистемам (i1,…,ip) системы {1,…,d}, и где ai1…ip – элементы поля ℙ, а d – размерность векторного пространства. Таким образом, строгое определение дифференциальной формы должно включать некоторое перемножение дифференциалов с их последующим линейным комбинированием. Получаемое сопряженное пространство для касательного пространства в выбранной точке вкладывается в алгебраическую систему, содержащую как операцию умножения, так и векторные операции. Более того, для другой координатной системы в той же точке, новое выражение дифференциальной формы, полученное по правилам замены переменных, должно приводить к тому же алгебраическому объекту, т.е. не зависеть от выбора базиса. Этим требованием алгебра Грассмана полностью удовлетворяет, что и объясняет её естественность, как алгебраической системы.
Стоит также отметить, что алгебра Грассмана является вырожденным частным случаем более общей алгебраической структуры – алгебры Клиффорда. Метрика в алгебре Грассмана нулевая, что следует из соотношений, которые мы накладываем на образующие. Если бы мы имели дело с невырожденной метрикой, то одним из примеров алгебры Клиффорда, при соответствующем выборе соотношений для образующих, могла бы стать алгебра кватернионов, что, в свою очередь, приводит нас к наличию прямой связи между математическим аппаратом алгебр Клиффорда и спинорными группами. Алгебра Клиффорда – очень важная структура в математике супермногообразий, и мы обязательно вернемся к ней в дальнейшем.
Теперь мы опишем некоторую формальную локальную модель, которая потребуется нам для построения супермногообразия. Элементы из класса локальных моделей, которые будут описаны ниже, мы будем называть суперобластями. Дадим определение. Пусть M – топологическое пространство и 𝝠(q) – алгебра Грассмана, порожденная системой образующих ξ1,…, ξq.
Суперобластью U(mǀq) назовем пару (U, QUs), где U⊂M, а QUs(V) – кольцо формальных выражений вида
𝑓 = 𝑓0(x)·1 + 𝑓i1(x)ξi1 + … + 𝑓i1i2…iq(x)ξi1 ξi2… ξiq
где i k ∈ {1,…,q}, 1⩽ i1<…< i q ⩽q, а 𝑓i – гладкие функции (Ui → ℝm) на V⊂M.
Запись вида ajbj, как это обычно подразумевается в физике и математике, предполагает суммирование по индексу j, т.е. сумму вида ∑ajbj где j пробегает всё множество индексов. Понятно, что мы можем теперь рассмотреть порожденный таким кольцом пучок  .
.
Если рассматривать пучок Q в роли структурного пучка, то мы видим, что его сечения не являются функциями. И, на данный момент, проблема состоит в том, что у нас нет способа определять глобальные объекты через склеивание локальных объектов. Непрерывное отображение пространства не задает для нас правило переноса сечений структурных пучков вида  и простое определение морфизмов через непрерывные отображения пространств уже неприменимо. Поэтому приходится задавать морфизмы пространств и пучков отдельно, с минимальными условиями согласованности. Тогда, следуя данной логике, мы получаем категорию окольцованных пространств, где объектами являются пары (M, Q(M)), состоящие их топологического пространства M и структурного пучка колец Q(M) на M. Морфизмом Φ: (M, Q(M)) → (N, Q(N)) в данной категории является пара Φ=(φ, φ*) где φ – непрерывное отображение пространств, а φ* – набор гомоморфизмов колец
и простое определение морфизмов через непрерывные отображения пространств уже неприменимо. Поэтому приходится задавать морфизмы пространств и пучков отдельно, с минимальными условиями согласованности. Тогда, следуя данной логике, мы получаем категорию окольцованных пространств, где объектами являются пары (M, Q(M)), состоящие их топологического пространства M и структурного пучка колец Q(M) на M. Морфизмом Φ: (M, Q(M)) → (N, Q(N)) в данной категории является пара Φ=(φ, φ*) где φ – непрерывное отображение пространств, а φ* – набор гомоморфизмов колец
φ*V: QN(V) → QM(φ-1(V)),
по одному для каждого открытого множества V⊂N, такой, что для всякой пары V1⊂V2⊂N имеем равенство
ρǀφ-1(V2),φ-1(V1) φ*V2 = φ*V1 ρǀV2,V1
Обратим внимание на это равенство, в нем отражена формальная запись коммутативности между гомоморфизмами колец и ограничениями на множествах при непрерывных обратных отображениях, т.е. это равенство сводится к требованию коммутативности следующей диаграммы, где ρ, как всегда, оператор ограничения:
φ*V2
QN(V2) QM(φ-1(V2))
ρǀV2 ,V1 ρǀφ-1(V2) , φ-1(V1)
φ*V1
QN(V1) QM(φ-1(V1))
Мы немедленно превратим набор гомоморфизмов колец φ* в морфизм пучков, если положим для любых V⊂N и V1⊂V2⊂N два равенства
φ*(QM)(V) = QN(φ-1(V)) и ρǀV2,V1 = ρǀφ-1(V2),φ-1(V1)
при φ*(QM)(V2) → φ*(QM)(V1)
Тогда φ*(QM) – будет пучком колец на N, а φ* определяет морфизм пучков колец QN → φ*(QM). Здесь был сделан ряд символьных отождествлений, но без труда видно, что означает каждый символ.
Теперь нам необходимо понять, что будет для нас, в случае нашего формального кольца, означать обратимость его элементов. Для этого сделаем небольшое отступление, чтобы выписать нужные нам свойства из теории ассоциативных колец. Мы определяем тело, как кольцо с единицей, в котором каждый ненулевой элемент обратим. Впрочем, для определения тела достаточно, чтобы каждый ненулевой элемент обладал левым или правым обратным элементом. При условии коммутативности умножения тело является полем. Идеалом кольца называется аддитивная подгруппа, замкнутая относительно левого (правого) умножения на элементы кольца.
Существует теорема о гомоморфизме колец, утверждающая что если 𝑓: R → Ř – некоторый гомоморфизм колец, то образ данного гомоморфизма Im 𝑓 изоморфен факторкольцу по ядру гомоморфизма Im 𝑓 ≌ R∕Ker 𝑓. Эта простая, но очень важная теорема следует из аналогичной теоремы для аддитивных групп, для ее доказательства достаточно проверить, что данный гомоморфизм (изоморфизм для групп) сохраняет операцию умножения.
Теорема (о гомоморфизме колец). Пусть 𝑓: R → Ř гомоморфизм колец. Тогда Im𝑓≌R∕Ker𝑓. Более точно, имеется изоморфизм φ : Im 𝑓 → R∕Ker 𝑓, ставящий в соответствие каждому элементу b = 𝑓(a) ∈ Im 𝑓 смежный класс π(a) = a + Ker 𝑓.
Доказательство. Согласно теореме о гомоморфизме для групп отображение φ является изоморфизмом аддитивных групп. Остается только проверить, что оно сохраняет операцию умножения. Проверим это. Пусть 𝑓(x) = u, 𝑓(y) = v. Тогда 𝑓(xy) = uv и φ(uv) = π(xy) = π(x)π(y) = φ(u)φ(v). ∎
Кольцо R называется локальным (или вполне примарным), если оно содержит такой двусторонний идеал I, что факторкольцо R∕I является телом, а это, в свою очередь, означает, что I – наибольший левый (правый) идеал кольца R, отличный от самого кольца R. Отметим, что для локального кольца I совпадает с радикалом Джекобсона кольца R – который является, по определению, пересечением всех максимальных идеалов кольца. Для кольца с единицей равносильны следующие свойства:
(I) Кольцо R локально;
(II) Все необратимые элементы кольца R содержаться в отличном от R двустороннем идеале;
(III) Необратимые элементы кольца R образуют отличный от R двусторонний идеал;
(IV) Если r – элемент из кольца R, то r или 1-r – обратимый элемент (иногда говорят, что если x из кольца R принадлежит радикалу Джекобсона, то 1-xy обратим в R для любого y из кольца R);
(V) Сумма двух необратимых элементов необратима;
Примером локального кольца, не являющегося телом, служит подкольцо кольца ℚ, состоящее из всех рациональных чисел, у которых знаменатели не делятся на фиксированное простое число.
В дальнейшем мы будем называть кольцо R локальным, если оно содержит максимальный идеал I. Гомоморфизм локальных колец 𝑓: R → Ř будем называть локальным, если 𝑓 (IR) ⊂ IŘ , где I – соответствующий максимальный идеал.
В случае классических многообразий над топологическим пространством M мы можем видеть, что для кольца ростков Q(M)x единственный максимальный идеал Ix в этом кольце состоит из ростков функций, равных нулю в точке x. Это следует из того, что росток, который не обращается в нуль в точке x, обратим в кольце ростков Q(M)x и тех свойств локального кольца, которые мы отметили выше. Морфизмы классических многообразий сохраняют значения функций, т.е. φ*(𝑓)(x)= 𝑓(φ(x)) для любого ростка, которому принадлежит функция 𝑓 из кольца Q(N)φ(x) в точке φ(x).
Рассмотрим теперь морфизм (φ,φ*): (M,Q(M)) ⟶ (N,Q(N)) для класса топологических многообразий C0, заданный так, чтобы гомоморфизмы соответствующих колец ростков были гомоморфизмами локальных колец. Пучки Q(M) и Q(N) являются пучками ℝ-алгебр и для них определены гомоморфизмы колец в поле ℝ, т.е. каждая алгебра снабжена соответствующим гомоморфизмом. Покажем, что если φ* сохраняет структуру ℝ-алгебр или, другими словами, тождественно действует на постоянных функциях, то (φ,φ*) является классическим морфизмом, т.е. φ* восстанавливается по φ. В самом деле, функция φ*(𝑓) определяется своими значениями в пучке Q(N). Далее, если 𝑓(φ(x))=0, то φ*(𝑓)(x)=𝑓(φ(x)). И если 𝑓(φ(x))=c, то φ*(𝑓-c)(x)=(𝑓-c)(φ(x)) в силу локальности и т.к. φ*(c)=c. Отсюда получаем равенство φ*( 𝑓)(x)=𝑓(φ(x)) в общем случае.
Эти рассуждения подсказывают нам определение категории локально окольцованных пространств, объектами которой являются окольцованные пространства (M,Q(M)), где Q(M) – пучок коммутативных колец и для каждой точки x из M слой Q(M)x является локальным кольцом.
Морфизмами Φ: (M, Q(M)) ⟶ (N, Q(N)) в категории локально окольцованных пространств являются морфизмы (φ,φ*) соответствующих окольцованных пространств, таких, что для любой пары точек x∈M, φ(x)∈N соответствующее отображение φ*: Q(N)φ(x) ⟶ Q(M)x является локальным морфизмом колец.
Пусть теперь (M, Q(M)) – локально окольцованное пространство, тогда по любому сечению 𝑓∈QM(U) структурного пучка мы можем определить функцию с переменной областью значений
𝑓(x) = 𝑓 mod Ix ∈ Q(M)x/Ix = 𝕂(x), x∈U, Ix – соответствующий максимальный идеал
Эти значения также сохраняются при морфизмах локально окольцованных пространств. Точнее, по локальному морфизму φ*: Q(N)φ(x) → Q(M)x определяется морфизм полей φ*𝕂: 𝕂(φ(x)) → 𝕂(x) и значение f в точке φ(x) переходит в значение φ*( f) в точке x. Однако, и на это следует обратить внимание, при таком определении функции с переменной областью значений, она не определяется своими значениями. Объясняется это тем, что нильпотенты, т.е. элементы из кольца, которые обращаются в ноль при некотором минимальном индексе n (an=0), в структурном пучке принимают лишь нулевые значения, не зависимо от степени, в которой они встречаются.
Чтобы перейти к определению супермногообразий, нам также следует упомянуть о том, как вводится градуировка в алгебрах.
Пусть у нас есть некоторая алгебра A и G – некоторая абелева группа в аддитивной записи) и пусть алгебра А представима в виде прямой суммы ⊕g∈G Ag векторных пространств Ag, где множество индексов g состоит из элементов группы G. Если из принадлежности элементов а∈Ag и b∈Af следует, что произведение ab∈Ag+f, где g и f элементы группы G, то это определяет в алгебре А градуировку и она называется градуированной алгеброй. В качестве G иногда рассматривают также полугруппу, но мы будем пользоваться лишь нашим частным случаем градуировки. Элемент градуированной алгебры А называется однородным степени g если он принадлежит пространству Аg. Если элемент из градуированной алгебры А представим в виде суммы
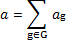
где  ∈Аg для каждого g∈G, то слагаемые называются однородными компонентами элемента a, а
∈Аg для каждого g∈G, то слагаемые называются однородными компонентами элемента a, а  называется однородной компонентой степени g элемента a. В градуированной алгебре А нулевой элемент является однородным элементом сразу всех возможных степеней. Если элемент a в градуированной алгебре отличен от нуля, то существует только одна степень g, такая, что а является однородным элементом степени g, которая и называется его степенью. Понятно также, что единица в градуированной алгебре всегда является однородным элементом степени 0. Так, например, алгебра матриц порядка n градуируется группой ℤn-1.
называется однородной компонентой степени g элемента a. В градуированной алгебре А нулевой элемент является однородным элементом сразу всех возможных степеней. Если элемент a в градуированной алгебре отличен от нуля, то существует только одна степень g, такая, что а является однородным элементом степени g, которая и называется его степенью. Понятно также, что единица в градуированной алгебре всегда является однородным элементом степени 0. Так, например, алгебра матриц порядка n градуируется группой ℤn-1.
Если в алгебре Грассмана символом ⋀ обозначить операцию внешнего умножения, то над произвольным полем 𝕂 она также имеет структуру градуированной алгебры, которую можно записать как
| ∞ | ||
| 𝝠(V) = 𝕂 ⊕ | ⊕ | ⋀rV |
| r=1 |
где ⋀rV подпространство векторного пространства V, r∈{0, 1, … , d}, порожденное элементами e1⋀…⋀ed, где d - размерность V, и называется внешней r-степенью пространства V, а элементы пространства ⋀rV называются r-векторами, над которыми можно далее вводить понятие тензора и строить содержательную физику.
Супермногообразия
Алгебра Грассмана не является коммутативной, поэтому суперобласти мы не можем отнести к локально окольцованным пространствам. Чтобы преодолеть это затруднение, нам понадобится перейти от коммутативных колец к суперкоммутативным кольцам. И тогда мы сможем построить обобщение локально окольцованного пространства, таким образом, чтобы включить формальные кольца из определения суперобласти, где присутствует алгебра Грассмана, в наше обобщение.
Пусть A – это ℤ2-градуированное кольцо, т.е. кольцо, представимое в виде суммы А=А0⊕А1 или, иначе, что его аддитивная группа является прямой суммой подгрупп четных и нечетных элементов, и что если f∈Ai, g∈Aj, то fg∈Ak, где k=i+j mod 2. Символ степени deg f=i означает принадлежность f к Ai. Определим суперкоммутатор [f, g] по формуле
[f, g] = fg − (-1)deg f deg g gf
для любой пары однородных элементов f, g из А и распространим его на все кольцо по биаддитивности. Тогда кольцо А назовем суперкоммутативным, если его суперкоммутатор [f,g]=0 для всех элементов этого кольца f, g.
Морфизмом ℤ2-градуированных, в частности, суперкоммутативных, колец, называется любой гомоморфизм, сохраняющий ℤ2-степень, а определение локального кольца и локального морфизма не меняется.
Тогда мы можем построить искомую категорию локально окольцованных суперпространств. Объектами категории локально окольцованных суперпространств являются окольцованные пространства (M, Q(M)), такие, что Q(M) – пучок суперкоммутативных колец, в котором все отображения ограничения сохраняют ℤ2-градуировку и все слои Q(M)x являются локальными кольцами для любой точки х. Морфизмами категории локально окольцованных суперпространств являются морфизмы соответствующих окольцованных пространств, такие, что все отображения φ*: Q(N)φ(x) ⟶ Q(M)x являются локальными морфизмами ℤ2-градуированных колец.
Теперь нам потребуется ввести понятие модельной категории и выяснить, что категория локально окольцованных суперпространств является модельной. Для этого мы зафиксируем категорию локальных пространств, т.е. пар пространств и локальных колец на них с соответствующими морфизмами. И пусть в этой категории выполнено единственное условие – вместе с пространством она содержит любое его открытое подпространство – такую категорию мы назовем модельной, а её объекты и морфизмы – модельными.
Далее, если у нас имеется фиксированная категория M модельных пространств, то категорией локально окольцованных пространств типа М называется совокупность локально окольцованных пространств (M,Q(M)) и их морфизмов, удовлетворяющих следующим трем условиям:
(I) Любая точка х∈M обладает окрестностью U, такой, что имеется изоморфизм локально окольцованных пространств
(φ, φ*): (U,Q(M)ǀU) ↔ (M,Q(M)),
где (M,Q(M)) – некоторое модельное пространство. Этот изоморфизм называется картой на M;
(II) Пусть имеется еще одна карта (ψ,ψ*): (V,Q(M)ǀV) ↔ (N,Q(N)), построенная также как в (I), но задающая новый изоморфизм, причем открытое подпространство V выбрано так, чтобы его пересечение с U было не пусто, т.е. U⋂V≠∅. Вполне естественно возникает новый морфизм (χ,χ*), который однозначно определяется из условия коммутативности следующей диаграммы:
(U⋂V, QǀU⋃V)
(φ,φ*) (ψ,ψ*)
(χ,χ*)
(MǀU⋂V,Q(M)ǀ U⋃V) (NǀU⋂V,Q(N)ǀ U⋃V)
и условие (II) состоит в том, чтобы морфизм (χ,χ*) был модельным, т.е. принадлежал модельной категории М. Этот модельный морфизм называется склейкой карт;
(III) Отображение (F, F*): (M, Q(M)) → (N, Q(N)) окольцованных пространств типа М, подчиняющихся условиям (I) и (II), называется морфизмом типа М, если любое его изображение (α,α*) с помощью карт на M и N является модельным, где под модельным изображением морфизма (F,F*) понимается морфизм (α,α*) в следующей диаграмме, делающей ее коммутативной:
(F, F*)ǀU
(U, Q(M)ǀU) (V, Q(N)ǀV)
(φ,φ*) (ψ,ψ*)
(α,α*)
(M,Q(M)) (N,Q(N))
Причем U⊂M, V⊂N, а также требуется, чтобы F(U)⊂V, или, в противном случае, карту (φ,φ*) следует задавать на пересечении U⋂F-1(V).
Пространства и морфизмы типа М образуют категорию, и все подпространства в данной категории устроены так же хорошо, например, в наследуемой при морфизмах гладкости, как и основное пространство. Однако не следует забывать, что всё это понимается в формальном категорном смысле и, что напрямую следует из определения модельной категории, относится только к открытым подпространствам. Мы пока не дали определение супералгебры, а данная конструкция, как и определение суперсхемы, для теории супермногообразий очень важна и будет далее введена и подробно рассмотрена. Без понятия супералгебры нельзя дать окончательное определение супермногообразия, в тех терминах, как оно сформулировано в современных работах. Но если следовать исторической логике, то уже возможно определить супермногообразие, понимая его как объект, изоморфный объекту из категории локально окольцованных суперпространств, где категория является одновременно модельной категорией. Для классических многообразий в качестве модельной категории выступила бы категория, где объекты – суть те самые локальные области, которые мы строили вводя локальные модели класса С0 и С∞. Вообще, категория локально окольцованных суперпространств содержит в себе категорию локально окольцованных пространств в качестве частного четного случая.
Итак, пусть у нас имеется пространство М и построенное на нем классическое многообразие размерности m, т.е. отображения областей покрытия устроены как 𝑓:Ui→ℝm. Будем называть это многообразие подстилающим. А также, пусть 𝝠(q) – алгебра Грассмана, порожденная системой образующих ξ1,…, ξq.
Гладким супермногообразием называется локально окольцованное пространство (M, Q(M)), у каждой точки которого имеется такая открытая окрестность U, что (U, QM(U)) изоморфно некоторой суперобласти U(mǀq) в модельной категории суперпространств, локально окольцованных ℝ-алгебрами.
В рамках данного определения супермногообразия, мы иногда будем писать, для удобства, что размерность dim(M,Q(M))=mǀq. И, иногда, будем обозначать супермногообразие символом Mmǀq, а пучок Q(M), при таком символьном обозначении гладкого супермногообразия, как С∞(Mmǀq).
Для того чтобы совершить краткий обзор других определений супермногообразия, представляющих на сегодняшний день скорее исторический, чем практический интерес, нам необходимо сделать небольшое отступление, связанное с темой локальных колец, а также ввести понятие представимого функтора. Напомним, что банаховым пространством называется полное нормированное векторное пространство, такое, что каждая фундаментальная последовательность имеет предел, также принадлежащий этому пространству. Соответственно определим банахову алгебру B, как ассоциативную алгебру, являющуюся одновременно банаховым пространством. С каждой коммутативной банаховой алгеброй В связано множество М(В) её максимальных идеалов, отличных от В. Имеется интересная интерпретация точки, как характера алгебры В при преобразованиях Гельфанда. Поскольку преобразования Гельфанда относятся к комплексному случаю, мы тоже на время будем считать комплексное поле ℂ основным полем. Тогда можно рассматривать множество максимальных идеалов М(В), как совокупность всех ненулевых гомоморфизмов В на ℂ, называемых также ненулевыми характерами. Действительно, если χ:B→ℂ – характер, то χ-1(0) – максимальный идеал в B. Обратно, если J∈М(В), то B/J – банахово поле над ℂ.
Теорема Гельфанда-Мазура утверждает, что всякое банахово поле над комплексным полем ℂ совпадает с самим полем ℂ и значит B/J=ℂ. Таким образом, каноническая проекция B→B/J даёт нам характер. Следовательно, мы можем интерпретировать точки χ, как характеры алгебры B и, поэтому, можем ставить в соответствие каждому элементу x∈B функцию x ̅ на множестве максимальных идеалов M(B) по формуле x ̅(χ)=χ(x). Функция x ̅ называется преобразованием Гельфанда элемента x.
В следующей части мы подробно рассмотрим понятие спектра, здесь мы лишь дадим его краткое определение, необходимое для понимания теории Гельфанда, справедливое для комплексного случая. Спектром элемента из банаховой алгебры x∈B мы будем называть множество Spec(x) тех λ∈ℂ, для которых x-λ·1 не имеет обратного в B. Поскольку, по лемме Цорна, всякий необратимый элемент содержится в некотором максимальном идеале, то множество значений x ̅ совпадает со спектром Spec(x). В результате мы имеем гомоморфизм x ̅:B→C(M(B))в алгебру всех непрерывных функций, определенную на множестве максимальных идеалов на M(B). Если мы, в качестве примера, рассмотрим B=C(X) – алгебру непрерывных функций на компакте X, то тогда M(B) изоморфно X, поскольку мы ставим в соответствие каждой замкнутой подобласти U⊂X некоторый замкнутый идеал J, состоящий из всех функций, обращающихся в ноль на данной подобласти U. Для всего компакта X мы имеем замкнутый идеал J, изоморфный всем функциям, нулевым на X, т.е. “глобальному нулю” на X. Понятно, что мы должны рассмотреть лишь точки и связанные с ними константы, а, значит, x ̅ есть тождественное преобразование x ̅=x. Рассматривая же ноль на всем X, мы, в качестве прообраза, получаем все пространство X. Безотносительно к этому примеру, можно показать, что M(B) является ограниченным и слабо замкнутым подмножеством в банаховом пространстве B*, сопряженным к B, из чего следует, что M(B) – компакт.
Такая интересная интерпретация понятие точки в теории Гельфанда, сразу нашла свое место в работах, посвященных осмыслению понятия точки для супермногообразия, и привела к ряду полезных результатов, особенно для теоретической физики. Более подробное изложение теории Гельфанда можно найти в книгах Н.Бурбаки (в разделе, посвященному спектральной теории), а также в книгах А.А.Кириллова и самого И.М.Гельфанда (см. список литературы). Добавим также, что в рамках теории банаховых алгебр, наиболее важные результаты для супермногообразий следуют из некоммутативной версии теоремы Гельфанда-Наймарка. А это предполагает, что мы изначально должны рассматривать алгебру с некоторой внутренней симметрией. Таковой, для банаховых алгебр, является понятие инволюции. Примером инволюции в алгебре B(H), для некоторого гильбертова пространства Н, может служить переход к гильбертову сопряженному оператору.
Все последние рассуждения мы делали в предположении, что основное поле у нас комплексное. Если перейти к произвольному полю, можно заметить что понятие точки можно всегда интерпретировать в категорном смысле. Находясь в категории множеств Set, можно отождествить любое множество Х с множеством Hom(e,X), где e – множество из одного элемента. Аналоги объекта е в теории категорий называются синглетонами. В абстрактной категории А синглетона может и не быть, но совокупность морфизмов HomA(Y,X) для всех Y уже несет полную информацию об объекте X с точностью до изоморфизма. В этом контексте, совокупность морфизмов φ:Y→X мы будем называть Y -точками объекта Х. Данное рассуждение мотивирует нас сделать определение представимого функтора, которое получается при формализации понятия Y-точки. Для категории множеств Set введем категорию функторов A ̅=Funct(A °,Set), объектами которой являются функторы из двойственной категории A ° в категорию множеств Set. Рассмотрим теперь функтор ℵX:A °→Set, ℵX(Y°)=HomA(Y,X), как объект из категории A ̅. Функтор ℱ∈A ̅ называется представимым, если он изоморфен функтору вида ℵX для некоторого X∈ObA. В этом случае говорят, что объект X представляет функтор ℱ. Основываясь на лемме Йонеды из теории категорий (доказательство см. ниже) можно показать, что если функтор из A ̅ представим, то представляющий его объект X определен однозначно, с точностью до канонического изоморфизма. Иногда, однозначность представляющего объекта выводят из существования универсального элемента – еще одного понятия из теории категорий, но это, если опустить детали, одно и то же, поскольку функтор, допускающий универсальный элемент, представим.
Другими словами, функтор ℱ: A ⟶ Set является представимым, если он естественно изоморфен Hom-функтору Hom(Y,−) который, для некоторого объекта Y из категории А, отправляет объекты Х в множества Hom(Y,Х). Соответственно, контравариантный функтор ℬ: А ⟶ Set, является представимым, если он естественно изоморфен контравариантному Hom*-функтору Hom(−,Y), который, для некоторого объекта Y из А, отправляет объекты Х в множества Hom(Х,Y). Интересно, что забывающие функторы в Set, которые мы рассматривали ранее в примерах, часто бывают приводимы. Так, забывающий функтор из категории Top топологических пространств и непрерывных отображений между ними в Set представим топологическим пространством из одного элемента.
Из определения супермногообразия понятно, что ни о каких его “точках”, в классическом понимании, мы говорить не можем, поэтому именно язык Y-точек оказывается достаточно полезным. Пусть K, M и N – супермногообразия произвольной размерности. К-точку супермногообразия М мы можем определить, как элемент множества Hom(K,M). В случае отображения φ:M→N, К-точки супермногообразия М переходят в К-точки супермногообразия N. Таким образом, у нас имеется отображение φM:Hom(K,M)→Hom(K,N), где φM(a)=(a), a∈Hom(K,M). Функтор точек, из категории функторов описанных выше, это просто сопоставление K↔Hom(K,M). Интересно, в связи с этим, понятие виртуального супермногообразия, которое рассматривал Д.А.Лейтес в одной из своих первых монографий, посвященных суперкоммутативному анализу.
Имеется еще один интересный подход к формализации понятия “точки” для супермногообразия. Под Λ-точкой супермногообразия Мmǀn мы можем понимать гомоморфизм C∞(Мmǀn)→Λ из гладко супермногообразия в алгебру Грассмана, описываемого равенствами Λ=Λ0⊕Λ1=C∞(ℝ0ǀN)=C(ℝ). Здесь мы использовали принятые нами ранее символьные отождествления. Из последнего равенства следует, что определяющий гомоморфизм можно переписать в виде ℝ0ǀN→Мmǀn. Использование этого гомоморфизма дает нам право говорить о “точках”, в которых принимают значения функции на супермногообразии М, а именно, функции на Мmǀn принимают значения во всех Λ-точках Мmǀn. Такой подход использовал в своей работе Ф.Ф.Воронов. Было показано, что множество {М(Λ)} всех Λ-точек данного супермногообразия Мmǀn имеет структуру гладкого конечномерного многообразия размерности dim{M(Λ)}=2N-1(n+m), где N>0.
В физике часто упоминается определение супермногообразия, идущего от работ Брайса Де Витта. Это класс многообразий над алгеброй Грассмана Λ, совпадающий с классом многообразий {М(Λ)} Λ-точек. Для построения такого класса задается аугментация ε:Λ→ℝ. Термин аугментация (своего рода приращение, увеличение) принадлежит теории гомологий симплициальных комплексов. Мы пока опустим определение аугментации, поскольку нам, на данный момент изложения, не хватает многих предварительных рассуждений, и заметим лишь, что цепной комплекс с аугментацией всегда обладает нетривиальной нульмерной группой гомологий. Для построения супермногообразия Де Витта в качестве областей берутся подмножества суперпространства U⊂(Λ)mǀn=(Λ0)m⨯(Λ1)n в смысле топологии по аугментации ε. Коэффициенты у функций перехода 𝑓:U→Λ являются грассманово-аналитическими продолжениями соответствующих гладких функций. Получающаяся алгебра функций, рассматриваемая, например, в работах А.Роджерс, обозначается H∞. Переход от супермногообразия Де Витта к супермногообразию, в терминах уже введенного нами определения, осуществляется через следующее равенство – это пара:
(X, QX(U) ) = (X0, Q∞X(U0⊂X0) ≡ H∞( ε-1(U0) ⊂ X) ).
Еще один класс супермногообразий, более широкий, чем H∞, образуют многообразия типа G∞-супермногообразий, или, аналогичные им, многообразия, рассматриваемые в работах В.С.Владимирова и И.В.Воловича. Эти супермногообразия определяются как топологические пространства, локально изоморфные U⊂(B)mǀn=(B0)m⨯(B1)n, где B – банахова коммутативная алгебра, а функции перехода B-гладкие, или, иногда, Λ-гладкие. Но, при таком подходе, возникают трудности в определении производных по нечетным координатам ∂∕∂ξ, чтобы ввести аналог векторного поля. Попытка исправить ситуацию, сделанная, М.Ротштейном, вновь возвращает нас к определению в терминах окольцованных пространств.
Самый общий подход к определению супермногообразия был предложен в работах А.С.Шварца. Супермногообразия определяются, в данном подходе, как функторы, действующие на категории алгебр Грассмана Λ→F(Λ)∈ObSet. При разумных ограничениях, мы можем получить из данного подхода определение супермногообразия в терминах окольцованных пространств. Но, если ограничения не вводятся, то данный подход либо еще мало исследован, либо вообще не может привести к каким либо интересным результатам именно в силу своей общности.
Чтобы завершить краткий обзор различных подходов к построению супермногообразий, дадим еще одно определение, вводимое через чисто четное суперпространство Mrd. Пусть (М,Q(М)) – суперпространство и пусть у нас имеется JM=Q(M)1+[Q(M)1]2 – пучок идеалов в Q(М)). Тогда Gr0Q(M)=Q(M)∕JM – пучок колец и пара (M,Gr0Q(M))=Mrd – чисто четное суперпространство и можно дать следующее определение супермногообразия, эквивалентное нашему основному определению гладкого супермногообразия. Дифференцируемым супермногообразием мы назовем локально расщепимое суперпространство (М,Q(М)), такое, что Mrd изоморфно обычному четному многообразию соответствующего класса (в нашем основном определении – бесконечно дифференцируемому). Локальная расщепимость означает, что у каждой точки x∈M есть открытая окрестность U, такая, что в паре (U,Q(М)|U) пучок Q(М)|U устроен достаточно хорошо в смысле коммутативности и гладкости переходов от одной окрестности к другой. Тогда супермногообразие мы можем представлять себе как суперпространство с локальными системами четно-нечетных координат. В качестве нечетных координат мы, в данном подходе, берем локальный базис сечений пучка, осуществляющего локальное расщепление. Определение расщепимости означает, в свою очередь, что между четными и нечетными координатами нет никаких других соотношений, кроме следствий суперкоммутативности. Расщепимые супермногообразия рассматривал в своих работах Ю.И.Манин, а также В.В.Молотков, который называл их векторизуемыми. В комплексном случае существуют аналитические супермногообразия и суперсхемы, которые не являются расщепимыми, препятствия для расщепимости ввел в своих работах В.П.Паламодов, а А.Л.Онищик подробно рассмотрел конкретные примеры данной задачи.
К вопросам локальной расщепимости для суперпространств мы еще вернемся, а лемму Йонеды (лемма носит имя японского математика Yoneda Nobuo), на которую мы сослались, вводя понятие представимого функтора, невозможно оставить без доказательства и в силу её фундаментальной важности для теории категорий и в силу её математической красоты. Итак, пусть С – некоторая категория, X∈Ob(C) – объекты этой категории и ℱ:C⟶Set– ковариантный функтор из нашей заданной категории в категорию множеств. Перед нами ставится задача описать все естественные преобразования Hom C(X,−)⟶ℱ соответствующего Hom-функтора и функтора ℱ.
Теорема (Лемма Йонеды). Все естественные преобразования Hom C(X,−)⟶ℱ находятся во взаимно однозначном соответствии с элементами функтора x∈ℱ(X).
Доказательство. Если задано естественное преобразование τ: Hom C(X,−)⟶ℱ, то рассмотрим отображение Hom C(X,X)  ℱ. Его значением на элементе 1X∈Hom C(X,X) будет некоторый элемент x∈ℱ(X), такой, что x =τX(1X)
ℱ. Его значением на элементе 1X∈Hom C(X,X) будет некоторый элемент x∈ℱ(X), такой, что x =τX(1X)
Если теперь задан элемент x∈ℱ(X), то определим естественное преобразование τ:Hom C(X,−)⟶ℱ следующим образом. Для каждого Y∈Ob(C) зададим отображение Hom C(X,Y)  ℱ(Y) при котором X
ℱ(Y) при котором X  Y ↦ ℱ (
Y ↦ ℱ (  )(x)
)(x)
Теперь проверим его естественность, она следует из коммутативности двух следующих диаграмм:
Hom C(X,Y) 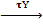 ℱ(Y)
Hom C(X,g) ℱ(g)
Hom C(X,Z) ℱ(Y)
Hom C(X,g) ℱ(g)
Hom C(X,Z)  ℱ(Z) ℱ(Z)
| Диаграмма для элементов
 ℱ ( ℱ (  )(x) )(x)
 g ℱ ( g ℱ ( 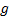 )(ℱ ( )(ℱ (  )(x)= ℱ ( )(x)= ℱ ( 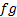 )(x) )(x)
|
В завершении проверим, что все наши сопоставления являются взаимообратными. Действительно, элементу x∈ℱ(X) соответствует естественное преобразование X  Y↦ℱ (
Y↦ℱ (  )(x). Этому преобразованию соответствует элемент ℱ(1X)(x)=1ℱ(X) (x)=x.
)(x). Этому преобразованию соответствует элемент ℱ(1X)(x)=1ℱ(X) (x)=x.
В свою очередь, естественному преобразованию τY: X  Y ↦ τY(
Y ↦ τY(  ) соответствует элемент τX(1X). Этому элементу соответствует естественное преобразование ωY:X
) соответствует элемент τX(1X). Этому элементу соответствует естественное преобразование ωY:X  Y↦ℱ (
Y↦ℱ (  )(τX(1X)). Причем
)(τX(1X)). Причем
ωY(f) = ℱ (  )(τX(1X)) = τY (Hom C(X,f)(1X)) = τY(f). ∎
)(τX(1X)) = τY (Hom C(X,f)(1X)) = τY(f). ∎
Отсюда мы сразу получаем, что каждое естественное преобразование Hom C(Y,−)⟶Hom C(X,−) имеет вид Hom C(f,−) для некоторого морфизма X  Y.
Y.
Иногда, в качестве доказательства леммы Йонеды, используют следующую наглядную диаграмму:
Hom(A,f)
Hom(A,A) Hom(A,X)
idA f
𝛹A 𝛹X
u (ℱf)u= 𝛹X(f)
ℱ (A) ℱ (X)
ℱf
Она выглядит на первый взгляд даже более привычно, если учесть что для ковариантного случая мы изначально помещали объект для Hom-функтора на второе место в скобках, а в основном доказательстве леммы он занимал первое место, что, конечно, никак не изменило сути доказательства. Итак, если мы имеем диаграмму, приведенную выше, то доказательство леммы сводится к утверждению её коммутативности. Здесь в качестве A выбран объект из произвольной малой категории, ℱ:C⟶Set – ковариантный функтор из нашей заданной категории в категорию множеств и через 𝛹 обозначены естественные преобразования, действующие на соответствующих морфизмах, так же под f мы понимаем некоторый морфизм A  X. Действительно, диаграмма показывает нам, что естественное преобразование 𝛹 полностью определяется элементом из внутреннего квадрата u = 𝛹A(idA), т.к. для любого морфизма A
X. Действительно, диаграмма показывает нам, что естественное преобразование 𝛹 полностью определяется элементом из внутреннего квадрата u = 𝛹A(idA), т.к. для любого морфизма A  X выполнено равенство 𝛹X(f) = (ℱf)uи это равенство задает естественное преобразование для любого элемента u ∈ ℱ(A).
X выполнено равенство 𝛹X(f) = (ℱf)uи это равенство задает естественное преобразование для любого элемента u ∈ ℱ(A).
Имеется ещё одна альтернативная формулировка леммы Йонеды, которая иногда является полезной. Пусть имеются два функтора N и E
N
Funct (C , Set)⨯C Set
E
действующие на соответствующих категориях и объектах этих категорий следующим образом: E(ℱ, X) = ℱ(X) и N(ℱ, X) = Nat(Hom C(X,−), ℱ), т.е. на всех естественных преобразованиях Hom C(X, −) в ℱ. Тогда лемма Йонеды утверждает существование естественного изоморфизма между функторами N и E.
Супералгебры и определение супермногообразия
В завершении первой части, мы дадим определение для супералгебр. Это нам необходимо не только для дальнейшего изложения, но и для того, чтобы сделать окончательное определение супермногообразия, которое на данный момент является общепринятым. И это совсем не означает, что определение супермногообразия, сделанное выше, имеет какие-либо существенные изъяны. Просто математическая полнота определения требует введения ряда дополнительных понятий.
Пусть M=M  ⊕M
⊕M  и N=N
и N=N  ⊕N
⊕N  – суперпространства и основное поле 𝕂 у нас произвольно, при этом характеристика поля char𝕂≠2. На пространствах M⊕N, M⊗N и Hom(M, N), введем градуировку следующим образом:
– суперпространства и основное поле 𝕂 у нас произвольно, при этом характеристика поля char𝕂≠2. На пространствах M⊕N, M⊗N и Hom(M, N), введем градуировку следующим образом:
(M⊕N)i = Mi⊕Ni,
(M⊗N)i =  Mj⊗Nk,
Mj⊗Nk,
Homi(M, N) = {F ∈ Hom(M, N) │ FMj ⊂ Nj+i}
где i, j, k ∈ ℤ2 и FMj ⊂ Nj+i ⟺FMj = FMj⋂N  ⊕ FMj⋂N
⊕ FMj⋂N  .
.
Элементы суперпространства Hom(M,N) называются гомоморфизмами, а морфизмами являются по определению только четные элементы суперпространства Hom(M,N). Соответственно морфизмы Hom(M,M) называются эндоморфизмами, а обратимые эндоморфизмы Hom(M,M) называются изоморфизмами.
Введём функтор в категории суперпространств Π, сопоставляющий каждому суперпространству его копию и, вместе с тем, делающий замену четности в суперпространстве по правилу (Π(M))  =M
=M  и (Π(M))
и (Π(M))  =M
=M  . Понятно, что суперпространства M и Π(Π(M)) отождествляются естественным образом. Функтор Π индуцирует каноническое нечетное отображение
. Понятно, что суперпространства M и Π(Π(M)) отождествляются естественным образом. Функтор Π индуцирует каноническое нечетное отображение
π: M ⟶ Π(M), m ⟼ π(m) , где m∈ M.
Отметим, что в работах по суперматематике принято четную и нечетную степени градуировки обозначать символами с надчеркиваниями – так, например, сумма собственных четных и нечетных подпространств записывается в виде M=M  ⊕M
⊕M  , однако иногда, в данной работе, четность пишется без надчеркивания, но, мы всегда обговариваем, что имеется в виду в тех редких случаях, когда это может привести к неоднозначной интерпретации.
, однако иногда, в данной работе, четность пишется без надчеркивания, но, мы всегда обговариваем, что имеется в виду в тех редких случаях, когда это может привести к неоднозначной интерпретации.
Супералгеброй A назовем ℤ2-градуированную ассоциативную алгебру с единицей, которая является суперпространством А с умножением-морфизмом A⊗A⟶A, заданном на суперпространстве A для любых его двух элементов.
Мы уже видели, когда рассматривали алгебру Грассмана, что единица принадлежит A  . Согласно определению четности в суперпространстве A⊗A для однородных элементов четность произведения равна сумме четностей этих элементов, т.е. p(ab)=p(a)+p(b), где а и b – однородные элементы супералгебры А, а p(*) – четность (parity – англ.) соответствующих элементов.
. Согласно определению четности в суперпространстве A⊗A для однородных элементов четность произведения равна сумме четностей этих элементов, т.е. p(ab)=p(a)+p(b), где а и b – однородные элементы супералгебры А, а p(*) – четность (parity – англ.) соответствующих элементов.
Суперкоммутатором назовем выражение вида [a,b] = ab – (-1)p(a)p(b)ba.
Супералгебра А называется суперкоммутативной если любые её два элемента суперкоммутируют, т.е. для любых a, b ∈A суперкоммутатор [a,b] = 0. Грассманова алгебра Λ является примером суперкоммутативной алгебры. Примером несуперкоммутативной алгебры является алгебра комплексных чисел ℂ (коммутативная над ℝ), в которой мнимая единица объявляется нечетной p(i)=  , обозначается такая несуперкоммутативная алгебра как ℂs (или иногда Q(ℝ)). В целом, для супералгебр можно ввести четыре вида симметрии относительно умножения, таким образом, мы можем различать:
, обозначается такая несуперкоммутативная алгебра как ℂs (или иногда Q(ℝ)). В целом, для супералгебр можно ввести четыре вида симметрии относительно умножения, таким образом, мы можем различать:
(I) Суперкоммутативные алгебры, где ba = (-1)p(b)p(a)ab,
(II) Суперантикоммутативные алгебры, где ba = – (-1)p(b)p(a)ab,
(III) Суперкосокоммутативные алгебры, где ba = (-1)(p(b)+1)(p(a)+1)ab,
(IV) Суперантикосокоммутативные алгебры, где ba = – (-1)(p(b)+1)(p(a)+1)ab.
Супертензорное произведение для супералгебр, в отличие от тензорного произведения суперпространств, вводится также с учетом четности. Супертензорным произведением супералгебр A и B назовем умножение задаваемое следующим способом:
(a ⊗ c)(b ⊗ d) = (−1)p(c)p(b) ab ⊗ cd, где a,b ∈A, c,d ∈B.
Супертензорное произведение суперкоммутативных супералгебр также является суперкоммутативной супералгеброй.
Теперь мы готовы дать финальное определение супермногообразия. Основное поле для данного определения выберем ℝ, а основное пространство M будем предполагать хаусдорфовым и со счетной базой.
Супермногообразием M назовем (супер)окольцованное пространство (M, QM), где QM – пучок суперкоммутативных супералгебр над топологическим пространством М и для каждой точки x∈М существует окрестность U⊂М, для которой суперпространство (U, QMǀU) диффеоморфно некоторой суперобласти (U, QU).
В данном определении присутствует понятие суперкоммутативной супералгебры, и в этом, по существу, единственное отличие, от того, что уже было сделано ранее. Как всегда, чтобы задать морфизм для окольцованных пространств, надо сделать это отдельно для отображения топологических пространств φ:M→N, входящих в определения супермногообразий и для морфизма пучков над этими пространствами. Поэтому, в терминах последнего определения, назовем морфизмом супермногообразий φ:M→N соответствующий морфизм суперпространств, сохраняющий четность супералгебр сечений. Морфизм супермногообразий называется диффеоморфизмом, если существует обратный морфизм ψ, такой что φ·ψ=idN и ψ·φ=idM. Многообразие Mrd=(M,QM) называется подстилающим многообразием и в зависимости от его свойств – связности, компактности и т.п. – так же называется и супермногообразие М.
Сделаем небольшое важное добавление, касающееся так называемого “правила знаков” в алгебраических супераналогах. Оно говорит о том, что при перестановке двух элементов четности p и q в равенствах появляется множитель (−1)pq. Важно помнить, что это правило верно, лишь, когда идет речь о перестановках соседних элементов, а не перестановке элементов в целом. Также следует быть внимательным, применяя это правило для преобразования левого или правого модуля над суперкоммутативной (и суперантикоммутативной) супералгеброй в двусторонний модуль. Имеется в виду следующее. Левый А-модуль – это суперпространство М с левым действие супералгебры А, задаваемой морфизмом A⊗M→M, для которого должны выполнятся равенства a(bm)=(ab)m и 1·m=m для любых a , b∈A и m∈M. Аналогично задается правый А-модуль для суперпространства М с правым действием M⊗A→M супералгебры А и двумя условиями для элементов, участвующих в данном морфизме. Понятие А-модуля является основным в теории представлений супералгебры А в суперпространстве М, оно определяет представление супералгебры в суперпространстве левыми и правыми операторами. Для преобразования левого А-модуля в правый А-модуль (и наоборот) над суперкоммутативной супералгеброй А следует воспользоваться формулой, использующей правило знаков:
ma =  am для любых m∈M и a∈A.
am для любых m∈M и a∈A.
Однако для функтора Π, делающего замену четности в суперпространстве M, А-модули для изоморфных пространств Π(М) и (М)Π вводятся формулами
Π(М) = Π(ℤ) ⊗ℤ M и (М)Π = M⊗ℤ Π(ℤ)
и при этом различны для левого и правого А-модулей если А не является полем (развернутое определение тензорного произведения над модулями мы сделаем во второй части). Поэтому левый А-модуль над суперкоммутативной супералгеброй А также можно превратить в правый (и наоборот) по формуле:
ma =  am для любых m∈M и a∈A.
am для любых m∈M и a∈A.
И обе эти формулы будут задавать согласованные структуры левого и правого А-модуля на суперпространстве М, а именно (am)b=a(mb) для любых a , b∈A и m∈M. Таким образом, мы можем снабдить любой левый или правый А-модуль над суперкоммутативной (и суперантикоммутативной) алгеброй А структурой двустороннего модуля сразу двумя способами. И это показывает насколько осторожным надо быть, используя “правило знаков” при работе с супералгебраическими конструкциями.
Часть 2.
Дата добавления: 2018-10-27; просмотров: 320; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
