Содержание и порядок выполнения
1. Вычертить в масштабе заданную схему вала с указанием размеров и величин нагрузок.
2. Определить окружные  и радиальные
и радиальные  усилия, приняв соотношение между ними
усилия, приняв соотношение между ними  .
.
3. Построить эпюры изгибающих моментов в вертикальной и горизонтальной плоскостях.
4. Построить эпюру суммарных изгибающих моментов.
5. Построить эпюру крутящих моментов.
6. Используя энергетическую теорию прочности, определить диаметры вала на отдельных участках и округлить их до стандартных размеров.
7. Вычертить эскиз.
Дано:  МПа,
МПа,  Н∙м,
Н∙м, 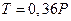 .
.
 м,
м,  м,
м,  м,
м,  м,
м,  м.
м.
Решение:
1) Вычертим схему вала с указанием всех заданных численных величин, рис. 9 а.
2) Определим окружные  и радиальные
и радиальные  усилия:
усилия:
 Н;
Н;
 Н.
Н.
Рассчитаем радиальные силы на колесах:
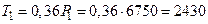 Н,
Н,
 Н.
Н.
Изобразим данные силы см. рис. 9 а.
3) Определим вертикальные и горизонтальные составляющие реакций подшипников (сечения  и
и  ). Для этого рассмотрим уравнения равновесия в каждой плоскости.
). Для этого рассмотрим уравнения равновесия в каждой плоскости.
Вертикальная плоскость (плоскость  ):
):
 ,
,
 Н.
Н.
 ,
,
 Н.
Н.
Проверка:
 .
.
Изобразим схему нагружения и построим эпюру изгибающих моментов  в плоскости
в плоскости  , рис. 9 б.
, рис. 9 б.
Горизонтальная плоскость (плоскость  ):
):
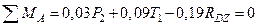 ,
,
 Н.
Н.
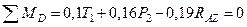 ,
,
 Н.
Н.
Проверка:
 .
.
Изобразим схему нагружения и построим эпюру изгибающих моментов 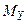 в плоскости
в плоскости 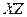 , рис. 9 б.
, рис. 9 б.
4) Рассчитаем суммарный изгибающий момент.
Суммарный изгибающий момент определяется по формуле:
 .
.
Запишем данный момент по сечениям.
|
|
|
Сечение  :
:  Н·м,
Н·м,
Сечение  :
:  Н·м,
Н·м,
Сечение  :
:  Н·м,
Н·м,
Сечение  :
:  Н·м.
Н·м.
Построим эпюру суммарных изгибающих моментов (см. рис.9 б). В действительности эпюра носит нелинейный характер, но в нашем случае можно её упрощённо представлять в виде линейной.
5) Построим эпюру крутящих моментов. Для этого найдём крутящие моменты на каждом участке и изобразим схему нагружения (см. рис. 9 а).
На участке  :
:  Н·м.
Н·м.
На участке  :
:  Н·м.
Н·м.
На участке  :
:  Н·м.
Н·м.
Строим эпюру крутящих моментов  (см. рис. 9 а).
(см. рис. 9 а).
6) Найдём значения расчётных моментов по четвертой (энергетической) гипотезе прочности. По этой гипотезе прочности расчётный момент высчитывается следующим образом:
 .
.
Запишем данный момент по сечениям.
Сечение  :
:  Н·м,
Н·м,
Сечение  :
:  Н·м,
Н·м,
Сечение  :
:  Н·м,
Н·м,
Сечение  :
:  Н·м,
Н·м,
Сечение  :
:  Н·м,
Н·м,
Сечение  :
:  Н·м.
Н·м.
Произведём расчёт диаметра вала исходя из условий прочности.
Условие прочности имеет вид:
 , где для круглого поперечного сечения
, где для круглого поперечного сечения  .
.
Тогда диаметр вала можно определить так:  .
.
На участке  .
.
 Н·м,
Н·м,  м
м  мм.
мм.
Округляем до стандартного значения  мм.
мм.
На участке  .
.
 Н·м,
Н·м,  м
м  мм.
мм.
Округляем до стандартного значения  мм.
мм.
На участке  .
.
 Н·м,
Н·м,  м
м  мм.
мм.
Округляем до стандартного значения  мм.
мм.
|
|
|
7) Вычертим эскиз вала, рис. 9 б.


Рис. 9 а.




Рис. 9 б.
Задача 10
Для заданной сжатой стойки требуется:
1. Вычертить схему стойки.
2. Определить допускаемую нагрузку сжатой стойки, если требуемый коэффициент запаса устойчивости  , материал стойки Ст.3 (
, материал стойки Ст.3 (  Па,
Па,  Па).
Па).
3. Исследовать влияние изменения длины стойки на величину допускаемой нагрузки (определить допускаемую нагрузку при длинах стойки  ,
,  ,
, 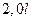 ).
).
Дано:  м, сечение – двутавр №24.
м, сечение – двутавр №24.
 Решение:
Решение:
1) Вычертим схему стойки.
2) Сечением стержня является двутавр №24 с характеристиками:  см2,
см2,  см.
см.
Определим гибкость стержня  , учитывая, что коэффициент приведения длины
, учитывая, что коэффициент приведения длины  для стержня с одним защемлённым и одним шарнирно опёртым концами равен
для стержня с одним защемлённым и одним шарнирно опёртым концами равен  :
:
 .
.
Для данной гибкости и данного материала (Ст.3) найдём путём интерполирования коэффициент  (например, из таблицы в книге Писаренко стр. 529):
(например, из таблицы в книге Писаренко стр. 529):  .
.
Величина предельной гибкости, ограничивающая применение формулы Эйлера, определяется для Ст.3 следующим образом:
 .
.
Т.к. гибкость рассматриваемого стержня 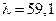 меньше предельной
меньше предельной 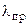 , то для определения критической силы будем использовать формулу Ясинского:
, то для определения критической силы будем использовать формулу Ясинского:
 МПа,
МПа,
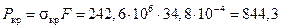 кН.
кН.
Учитывая запас устойчивости находим допускаемую нагрузку:
|
|
|
 кН.
кН.
Для заданной допускаемой нагрузки определим напряжения в стержне:
 Па.
Па.
Условие прочности при сжатии выполняется!
Проверим условие устойчивости:
 , где
, где  – коэффициент уменьшения основного допускаемого напряжения.
– коэффициент уменьшения основного допускаемого напряжения.
 .
.
 .
.
Условие устойчивости выполняется с погрешностью 5%.
3)
Исследуем влияние изменения длины стойки на величину допускаемой нагрузки.
Очевидно, что длина влияет на такой важнейший параметр как гибкость стойки. Определим допускаемые нагрузки при длинах стойки равных  ,
,  и
и  .
.
При длине стойки  :
:
 .
.
Т.к. гибкость рассматриваемого стержня меньше предельной  , то для определения критической силы будем использовать формулу Ясинского:
, то для определения критической силы будем использовать формулу Ясинского:
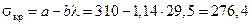 МПа,
МПа,
 кН.
кН.
Учитывая запас устойчивости находим допускаемую нагрузку:
 кН.
кН.
Очевидно, что чем меньше длина стойки, тем выше допускаемые нагрузки с точки зрения устойчивости.
При длине стойки  :
:
 .
.
Т.к. гибкость рассматриваемого стержня меньше предельной  , то для определения критической силы будем использовать формулу Ясинского:
, то для определения критической силы будем использовать формулу Ясинского:
 МПа,
МПа,
 кН.
кН.
Учитывая запас устойчивости находим допускаемую нагрузку:
 кН.
кН.
При длине стойки  :
:
 .
.
 Па.
Па.
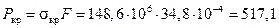 кН.
кН.
Учитывая запас устойчивости находим допускаемую нагрузку:
|
|
|
 кН.
кН.
Очевидно, что чем выше длина стойки, тем хуже её устойчивость.
Задача 11
На двутавровую балку, свободно лежащую на двух жёстких опорах, с высоты  падает груз
падает груз 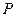 (см. рис.11, а). Требуется:
(см. рис.11, а). Требуется:
1. Найти наибольшее нормальное напряжение в балке.
2. Решить аналогичную задачу при условии, что правая опора заменена пружиной, податливость которой равна  .
.
3. Сравнить полученные результаты.
Дано:  кН, профиль – двутавр №30а,
кН, профиль – двутавр №30а,  см,
см,  м,
м,  м/кН.
м/кН.
Решение:
1)
Напряжение при ударе определяется по формуле:
 , где
, где  – динамический коэффициент при ударе,
– динамический коэффициент при ударе, 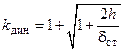 ,
,  – прогиб балки, лежащей на жёстких опорах, где приложена ударная нагрузка (при статическом действии силы).
– прогиб балки, лежащей на жёстких опорах, где приложена ударная нагрузка (при статическом действии силы).
При  ,
, 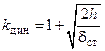 .
.
При  ,
,  .
.
Для определения  необходимо вычислить
необходимо вычислить  . Это можно сделать методом начальных параметров. Составим уравнения изгибающих моментов от статического действия силы
. Это можно сделать методом начальных параметров. Составим уравнения изгибающих моментов от статического действия силы 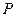 по участкам балки.
по участкам балки.
Определим реакции опор:
 ,
,  кН.
кН.
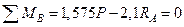 ,
,  кН.
кН.
Построим эпюру моментов.
Воспользуемся методом сечений. За начало отсчёта примем сечение  .
.
На участке  ,
,  м:
м:
 кН,
кН,  кН,
кН,  кН.
кН.
 кН∙м,
кН∙м,  кН∙м,
кН∙м,  кН∙м.
кН∙м.
На участке  ,
,  м:
м:
 кН,
кН,  кН,
кН,  кН.
кН.
 кН∙м,
кН∙м,
 кН∙м,
кН∙м,  кН∙м.
кН∙м.
Запишем уравнение прогибов:
 ,
,
где  – функция прогиба балки;
– функция прогиба балки;  – прогиб в начале координат;
– прогиб в начале координат; 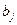 – координаты точек приложения сосредоточенных сил.
– координаты точек приложения сосредоточенных сил.
Приведём уравнения прогибов к конкретному виду:
 .
.
В уравнении указаны, какие слагаемые, на каких участках используются.
Определим  ,
,  , если известно, что в сечениях
, если известно, что в сечениях  и
и  прогибы отсутствуют (шарнирное опирание):
прогибы отсутствуют (шарнирное опирание):
 , откуда
, откуда  .
.
 ,
,
откуда  .
.
В итоге уравнения прогибов примет вид:
 .
.
Статический прогиб балки в сечении приложения силы  будет равен:
будет равен:
 .
.
Знак минус можно опустить, т.к. он указывает на то, что балка прогибается вниз.
Балка имеет двутавровый профиль с номером двутавра 30а:  см4,
см4,  см3,
см3, 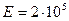 МПа.
МПа.
 м.
м.
Т.к.  , то
, то  .
.
 МПа.
МПа.
Следовательно,  МПа.
МПа.
2)
Решим эту задачу при наличии на правой опоре пружины (см. рис. 11, б). Осадка пружины под действием реакции на правой опоре  м.
м.
Тогда прогиб балки в точке приложения силы будет:  , где
, где 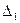 – перемещение балки как абсолютно жёсткого тела, определим его из подобия треугольников (см. рис. 11, б):
– перемещение балки как абсолютно жёсткого тела, определим его из подобия треугольников (см. рис. 11, б):  м
м  мм.
мм.
Т.о.  м.
м.
 .
.
 МПа.
МПа.
3)
Установка пружины значительно снижает напряжения, возникающие при ударе.

|

Рис. 11, б
Дата добавления: 2018-10-27; просмотров: 252; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
