Краевые задачи. Решение краевой задачи для линейного ДУ 2-го порядка методом функции Грина.
Опр.: Задача нахождения реш. д.у. F(x,y,y’,…,y(n))=0 xє[a,b] (1) удовл. усл-ям
Gi(a,y(a),y’(a),…,y(n-1)(a))=αi, i=1,…,m Gi(b,y(b),y’(b),…,y(n-1)(b))=αi, i=m+1,…,n (1<=m<n) (2)
наз. краевой задачей(кр. з.), условия (2) - краевыми условиями. Чтобы реш. краевую задачу (1),(2) надо найти общее решение y=y(x,c1,c2,…,cn) ур-ия (1) и подобрать значение произвольных постоянных входящих в ф-ию общ. реш.,так чтобы выполнялись для ф. y=y(x) краевые условия (2).
Рассм следующую кр. з.: a0(x)y'' + a1(x) y’+ a2(x)y=f(x), xє[a,b] (3) ; 
(4)
Функцией Грина краевой зад. (3), (4) наз. ф-ия G(x,s), определенная при xє[a,b] , s є[a,b] и при каждом фиксированном s є[a,b]обладающий свойствами:1)x≠s, G(x,s) удовлетворяет ур-ию a0(x)y'' + a1(x) y’+ a2(x)y=0 (3'); 2) G(x,s) удовл. усл. (4); 3) при x=s ф-ия G(x,s)-непрер. по x, а ее производная по x терпит разрыв 1го рода со скачком = 1/ a0(x):
| G(s+0,s)= G(s-0,s) Gx’(s+0,s) - Gx’(s-0,s)=1/a0(s) | (5) |
Реш. кр. з. (3)-(4) выражается формулой: 
(6)
Где G(x,s)= 
( ф-ция Грина), y1(x) –удовл.1-му условию в (4), y2(x) – удовл.2-му условию в (4)
Схема вывода формулы Грина:
1) Решение неоднор.урав-я (3) будем искать методом Лагранжа( методом вариации постоянных). Записываем решение в виде:
y(x) = C1(x)*y1(x) + C2(x)*y2(x) (7)
{y1, y2} – ФСР лин.однород.урав-я (3)
C1’(x)*y1 + C2’(x)*y2=0;
C1’(x)*y1’+C2’(x)*y2’ = f(x).
2) Решение этой системы (ф-лы Крамера) имеет вид:
C1'(x) = (-y2(x)*f(x))/W(x);
C2’(x) = (y1(x)*f(x))/W(x). (*)
Интегрируем урав-я (*), получаем:
C1(x) =∫ [(-y2(x)*f(x))/W(x)]*dx + q1;
C2(x) =∫ [(y1(x)*f(x))/W(x)]*dx + q1.
q1, q2 – const
3) Подставляем С1(x), C2(x) в (7), получим общее решение уравнения (3).
|
|
|
Требуя чтобы полученное решение удовлетворяло граничным условиям, получим формулу (6).
Пример . y’’-y’=f(x), y(0)=0, y'(1)=0. Подсказка: можно взять y1(x)=1-ex, y2(x)=1.
y’’-y’ = 0; k^2-k=0; k1=0; k2=1; y0 = C1 + C2*e^x
y(0)=0; y’(1)=0
y1(x)=1-e^x; y’0=C2*e^x, y2(x)=1;
W(y1, y2) = [1-e^x 1; -e^x 0] = e^x <> 0
G(x,s) = {(1-e^s)/e^s, 0<=s<=x; (1-e^x)/e^s, x<=s<=1}
ДУ в частных производных (ДУЧП) 1-го порядка. Линейные и квазилинейные ДУЧП. Метод первых интегралов при решении линейного однородного ДУЧП
Пусть искомая функция u=u( x1,…,xn ) (n≥2). Уравнение, связывающее искомую функцию, независимые переменные и частные производные от искомой функции, называется дифференциальным уравнением с частными производными. Оно имеет вид:
Здесь F- данная функция своих аргументов. Порядок старшей частной производной, входящей в уравнение, называется порядком этого уравнения.
Дифференциальное уравнение с частными производными первого порядка с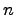 
независимыми переменными:
(*)
Решением уравнения (*) называется определенная в подобласти D области D(u) скалярная функция u, имеющая частные производные первого порядка по всем переменным и обращающая уравнение (*) в тождество относительно x = (x1, ..., xn) ∈ D. График решения u = u(x1, ..., xn) в пространстве R×Rn называется интегральной поверхностью уравнения (*).
|
|
|
Опр.: Линейным ур-м 1го порядка с частными производныи наз. ур-е) 
(1), гдеai(x1,…,xn), i=1,..,n, с(x1,…,xn), di(x1,…,xn)- заданные ф-ии определенные в обл. D Є Rn и U=U(x1,…,xn) - искомая ф-ия.
Опр.: Сис. обыкновенных диф. ур.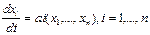 
(2) наз. системой ур-й характеристик для однородного ур-я (1), а ее реш. характеристикой.
Опр. Соотношение ψ(x1,x2,…xn) = C (*) ( где ψ – непрерыв. диффернц.функция, С- постоянная) называется 1-м интегралом системы x’i = fi(t,x1,..xn) i=1,n если при подстановки в него решения xi = xi(t) системы оно обращается в тождество.
Теор.: если ψi(x1,…,xn)=сi, i=1,..,n-1 независ. первые интегралы сис (2), то все реш. ур. (1) можно получить из формулы U=Ф(ψ1,…, ψn-1), где Ф-произвольная диффер. ф-ия.
Сис. обыкновенных диф. ур.
(2*) наз. системой ур-й характеристик для неоднородного ур-я (1)
Теор.: если ψi(x1,…,xn)=сi, i=1,..,n независ. первые интегралы сис (2*), то все реш. неоднородного ур. (1) можно получить из формулы (ψ1,…, ψn)=с, где Ф-произвольная диффер. ф-ия.
Дата добавления: 2018-10-27; просмотров: 393; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!