Структура общего решения линейного неоднородного ДУ n-го порядка.

Рассмотрим линейное неоднородное дифференциальное уравнение

y⁽ⁿ⁾ + a_n-1(x)y^{(n- 1)} + ... + a₁(x)y' + a₀(x)y = f(x).

Общим решением этого уравнения на отрезке [a;b] называется функция y = Φ(x, C₁,..., C_n ), зависящая от n произвольных постоянныхC₁,..., C_n и удовлетворяющая следующим условиям :

− при любых допустимых значениях постоянных C₁,..., C_n функция y = Φ(x, C₁,..., C_n ) является решением уравнения на [a; b] ;

− какова бы ни была начальная точка (x₀, y₀, y_1,0 ,..., y_{n − 1,0} ) , x₀∈ [a;b] , существуют такие значения C₁ =C₁₀ , ..., C_n = C_n0 , что функция y = Φ(x, C₁₀ , ..., C_n0) удовлетворяет начальным условиям y(x₀) = y₀, y '(x₀) = y_1,0 ,..., y^{(n − 1)} (x₀) = y_{n− 1,0} .

 

Справедливо следующее утверждение (теорема о структуре общего решения линейного неоднородного уравнения).

Общее решение лин.неоднородного ду есть y(x,C₁,..., C_n) = y₀(x) + y*(x), где y0 – решение лин.однрород. ду соотв.данному, y*(x) – частное решение неоднородного ду.

{ Если все коэффициенты уравнения линейного однородного дифференциального уравнениния непрерывны на отрезке [a;b] , а функцииy₁(x), y₂(x),..., y_n(x) образуют фундаментальную систему решений соответствующего однородного уравнения, то общее решение неоднородного уравнения имеет вид

y(x,C₁,..., C_n) = C₁ y₁(x) + C₂ y₂(x) + ... + C_n y_n(x) + y*(x),

где C₁,...,C_n — произвольные постоянные, y*(x) — частное решение неоднородного уравнения. }

Пример.

Рассмотрим линейное неоднородное дифференциальное уравнение с непрерывными на (e, ∞) коэффициентами и непрерывной правой частью

y’’-y = 2-x^2

y’’-y = 0, k^2 – 1 = 0;

k1,2 = +-1, y1 = e^x, y2 = e^-x.

 

частным решением неодродного является функция

y*(x) = A*x^2+B*x + C

y*(x) = x^2

Фундаментальную систему решений соответствующего однородного уравнения образуют функции y₁(x) = e^x , y₂(x) = e^-x.

Общее решение неоднородного уравнения имеет вид

Y(C1,C2, x) = C1*y1 + C2*y2 + y*(x)

Метод Лагранжа

Задача состоит в вычислении какого–либо частного решения линейного неоднородного дифференциального уравнения с непрерывными коэффициентами и непрерывной правой частью.

Рассмотрим линейное неоднородное дифференциальное уравнение

y⁽ⁿ⁾ + a_n-1(x)y^{(n- 1)} + ... + a₁(x)y' + a₀(x)y = f(x).

с непрерывными на [a; b] коэффициентами и непрерывной правой частью.

Предположим, что известна фундаментальная система y₁(x), y₂(x),..., y_n(x) решений соответствующего однородного уравнения y⁽ⁿ⁾ + a_n-1(x)y^{(n- 1)} + ... + a₁(x)y' + a₀(x)y = 0.

Будем искать частное решение неоднородного уравнения в виде

y*(x) = C₁(x) y₁(x) + C₂(x) y₂(x) + ... + C_n(x) y_n(x) ,

где C₁(x), C₂(x) , ... , C_n(x) — неизвестные, n раз дифференцируемые на [a; b] функции. Их называют варьируемые постоянные общего решения однородного уравнения.

Справедливо следующее утверждение.

Пусть y₁(x), y₂(x),..., y_n(x) — фундаментальная система решений однородного уравнения y⁽ⁿ⁾ + a_n-1(x)y^{(n- 1)} + ... + a₁(x)y' + a₀(x)y = 0 с непрерывными на отрезке [a; b] коэффициентами. Если правая часть f(x) неоднородного уравнения y⁽ⁿ⁾ + a_n-1(x)y^{(n- 1)} + ... + a₁(x)y' +a₀(x)y = f(x) непрерывна на [a; b], то его частное решение можно искать в виде

y*(x) = y(x,C₁,..., C_n) = C₁(x) y₁(x) + C₂(x) y₂(x) + ... + C_n(x) y_n(x) .

Неизвестные функции C₁(x), C₂(x) , ... , C_n(x) находятся из системы

Такой метод отыскания частного решения неоднородного уравнения называется методом вариации произвольных постоянных илиметодом Лагранжа.

Подробнее (кому нужно)

Посмотрим как можно найти методом Лагранжа частное решение для уравнения 2–го порядка y'' + a₁(x)y' + a₀(x)y = f(x) с нерерывными коэффициентами и непрерывной правой частью.

Предположим, что известна фундаментальная система y₁(x), y₂(x) решений соответствующего однородного уравнения y'' + a₁(x)y' + a₀(x)y =0.

Будем искать частное решение неоднородного уравнения в виде

y*(x) = C₁(x) y₁(x) + C₂(x) y₂(x),

где C₁(x), C₂(x) — такие неизвестные,дважды дифференцируемые на [a; b] функции.

Для того чтобы подставить функцию y*(x) в исходное уравнение, найдём сначала первую производную y*(x):

(y*(x))' = C₁'(x) y₁(x) + C₁(x) y₁'(x) + C₂'(x) y₂(x) + C₂(x) y₂'(x).

Будем искать C₁(x), C₂(x) такими, чтобы C₁'(x) y₁(x) + C₂'(x) y₂(x) = 0 и, следовательно,

(y*(x))' = C₁(x) y₁'(x) + C₂(x) y₂'(x).

Тогда

(y*(x))'' = C₁'(x) y₁'(x) + C₁(x) y₁''(x) + C₂'(x) y₂'(x) + C₂(x) y₂''(x).

Подставим выражения для производных в уравнение:

y'' + a₁(x)y' + a₀(x)y ≡ C₁'(x) y₁'(x) + C₁(x) y₁''(x) + C₂'(x) y₂'(x) + C₂(x) y₂''(x) + a₁(x)(C₁(x) y₁'(x) + C₂(x) y₂'(x)) + a₀(x)(C₁(x) y₁(x) + C₂(x)y₂(x))= f(x).

После простых преобразований имеем:

C₁(x)(y₁'' + a₁(x)y₁' + a₀(x)y₁) + C₂(x)(y₂'' + a₁(x)y₂' + a₀(x)y₂) + C₁'(x) y₁'(x) + C₂'(x) y₂'(x) = f(x).

Но поскольку y₁(x), y₂(x) — решения однородного уравнения y^'' + a₁(x)y' + a₀(x)y = 0, то

C₁'(x) y₁'(x) + C₂'(x) y₂'(x) = f(x).

Для неизвестных функций C₁(x), C₂(x) получили систему линейных дифференциальных уравнений второго порядка:

Определитель этой линейной относительно C₁'(x), C₂'(x) системы — это отличный от нуля на [a; b] вронскиан фундаментальной системы решений.

Следовательно, система имеет единственное решение, которое можно выписать в явном виде (имеем два дифференциальных уравнения первого порядка):

Эти дифференциальные уравнения первого порядка с разделяющимися переменными легко интегрируются:

Неизвестные варьируемые постоянные найдены — найдено частное решение линейного неоднородного уравнения второго порядка.

Пример

Найдём методом Лагранжа (методом вариации произвольных постоянных) частное решение линейного неоднородного дифференциального уравнения второго порядка

с непрерывными на (e, ∞) коэффициентами и непрерывной правой частью.

Фундаментальную систему решений соответствующего однородного уравнения образуют функции y₁(x) = ln x , y₂(x) = x.

Будем искать частное решение неоднородного уравнения в виде y*(x) = C₁(x) lnx + C₂(x) x:

Подставим выражения для производных в уравнение:

Для неизвестных функций C₁(x), C₂(x) получили систему линейных дифференциальных уравнений второго порядка:

Окуда имеем:

И тогда частным решением исходного уравнения второго порядка является функция y*(x) = C₁(x) lnx + C₂(x) x:

---

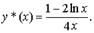
Дата добавления: 2018-10-27; просмотров: 578; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!