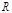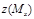Список использованных источников
1. Климат Хабаровска: климатический справочник / Ц. А. ШВЕР. – Ленинград: Гидрометеоиздат, 1981. – 252 с.
2. Зимнее содержание автомобильных дорог Дальнего Востока: учеб.пособие / В. А. Ярмолинский. – Хабаровск: Изд – во Тихоокеан. гос ун-та, 2012. – 207с.
3. Справочник по климату СССР. Вып. 25. Хабаровский край. Часть 4. Влажность воздуха. Атмосферные осадки. Снежный покров. – Л. : гид-рометеоиздат, 1968. – 239с.
4. Стандарт организации. Технологический регламент на проведение работ по очистке от снега автомобильных дорог регионального и межмуниципального значения Хабаровского края.- Разработан сотрудниками Тихоокеанского государственного университета и ООО «Прогресс» / А. И. Ярмолинский, В. А. Ярмолинский, В. В. Лопашук, А. В. Лопашук. – Хабаровск, 2012. – 62 с.
К. С. Ку (ТПЗ(м)-51)
А. Д. Ловцов (д-р техн. наук, профессор)
ОБ ОПРЕДЕЛЕНИИ РАЗМЕРОВ КОНЕЧНЫХ ЭЛЕМЕНТОВ,
ОБЕСПЕЧИВАЮЩИХ НЕОБХОДИМУЮ ТОЧНОСТЬ РАСЧЕТОВ
Метод конечных элементов (МКЭ) является в настоящее время основным методом расчета строительных конструкций и сооружений. В результате решения системы уравнений МКЭ получаются приближенные значения искомой функции в узлах конечных элементов. В этой статье рассматриваются: вопросы определения погрешности и уточнения значений приближенных решений; определение размеров конечных элементов, обеспечивающих необходимую точность расчетов. Излагается малоизвестный метод Шварцмана, позволяющий эффективно получать двусторонние оценки неизвестного точного решения и находить погрешность приближенного решения [1].
|
|
|
Согласно теореме Шварцмана [2]: Если последовательность
 (1)
(1)
монотонно сходится к  , то точное решение
, то точное решение  принадлежит отрезку
принадлежит отрезку
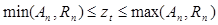 (2)
(2)
где:  – значение приближенного решения в некотором узле;
– значение приближенного решения в некотором узле;  – значение точного решения в этом же узле;
– значение точного решения в этом же узле;
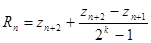 ;
;  . (3)
. (3)
Из неравенства (2) следует, что, если в качестве приближенного решения взять
 (4)
(4)
то справедлива следующая оценка погрешности:
 (5)
(5)
Формулы (4), (5) и составляют содержание метода Шварцмана. Подчеркнем, что оценка погрешности не содержит неопределенных постоянных.
Алгоритм получения оценки точности решения по методу Шварцмана состоит из следующих действий.
Проводится численный эксперимент: на грубой сетке КЭ производится первый расчет, результаты которого обозначим  . Следующие расчеты выполняются со сгущением сетки конечных элементов (например, в 2 раза). Обозначим результаты расчетов соответственно:
. Следующие расчеты выполняются со сгущением сетки конечных элементов (например, в 2 раза). Обозначим результаты расчетов соответственно:  ,
,  и т. д. (рис.1). Под
и т. д. (рис.1). Под  подразумевается, например, перемещение одной и той же точки, полученное расчетом на n-ой сетке. Расчеты на последовательно сгущаемых сетках повторяются необходимое число раз. Минимальное число расчетов – три.
подразумевается, например, перемещение одной и той же точки, полученное расчетом на n-ой сетке. Расчеты на последовательно сгущаемых сетках повторяются необходимое число раз. Минимальное число расчетов – три.
|
|
|
Далее по теореме Шварцмана: из равенства  определяется
определяется  ; рассчитываются величины
; рассчитываются величины  ,
,  ; по (4) находится значение приближенного решения с оценкой его погрешности (5).
; по (4) находится значение приближенного решения с оценкой его погрешности (5).



Рис. 1. Перемещение точки на сгущаемой сетке
 Пример 1. Рассмотрим шарнирно опертую по контуру пластину с размерами 3х6 м (рис. 2). Модуль упругости
Пример 1. Рассмотрим шарнирно опертую по контуру пластину с размерами 3х6 м (рис. 2). Модуль упругости  = 3.06·106 т/м2 , коэффициент Пуассона
= 3.06·106 т/м2 , коэффициент Пуассона  =0.2, толщина пластины
=0.2, толщина пластины  =0.2 м., объемный вес – 2.5 т/м3. Поскольку проводится линейный расчет, нагрузку принимаем увеличенной (
=0.2 м., объемный вес – 2.5 т/м3. Поскольку проводится линейный расчет, нагрузку принимаем увеличенной ( 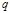 =10000 кН/м2) с тем, чтобы посредством ПК ЛИРА получить Рис. 2. Расчетная схема
=10000 кН/м2) с тем, чтобы посредством ПК ЛИРА получить Рис. 2. Расчетная схема
результаты с большим количеством
значащих цифр. В соответствии с алгоритмом метода Шварцмана были выбраны шаг разбиения сетки и количество расчетов. Первый расчет выполнялся для сетки 4х8 с размером элемента 0,75 м. Следующие расчеты выполнялись со сгущением сетки конечных элементов в два раза: сетки 8х16, 16х32, 32х64, 64х128.
|
|
|
После расчетов, проведенных в ПК ЛИРА, необходимо выбрать во всем множестве точек (узлов) пластины ту, по значениям которой будет оцениваться точность решения задачи. В нашем случае выбрана точка в середине пластины. Величины изгибающих моментов  ,
,  и прогиба
и прогиба  в выбранной точке приведены в табл. 1
в выбранной точке приведены в табл. 1
Таблица 1
Данные численного эксперимента
| n |
|
|
|
| 4х8 | 5719.7 | 2187.38 | -272.018 |
| 8х16 | 6318.89 | 2406.62 | -267.497 |
| 16х32 | 6467.65 | 2462.9 | -266.347 |
| 32х64 | 6504.78 | 2477.07 | -266.058 |
| 64х128 | 6514.06 | 2480.62 | -265.986 |
Применяя метод Шварцмана к нашим данным, получим оценку точности приближенного решения. Значение приближенного решения (  ) в рассматриваемом узле пластины приведено во втором столбце таблиц 2, 3 и 4. По столбцу 3 табл.2 видим, что последовательность
) в рассматриваемом узле пластины приведено во втором столбце таблиц 2, 3 и 4. По столбцу 3 табл.2 видим, что последовательность  монотонно сходится к 4. Поскольку
монотонно сходится к 4. Поскольку  , то
, то  . В столбцах 4, 5 приведены значения
. В столбцах 4, 5 приведены значения 
 ,рассчитанные по (3). В двух последних столбцах приведены приближенное решение
,рассчитанные по (3). В двух последних столбцах приведены приближенное решение  по (4) и оценка его погрешности
по (4) и оценка его погрешности  по (5).
по (5).
Таблица 2
Оценка точности определения перемещений 
|
|
|
|
|
|
|
| ||
| 4х8 | -272.018 | |||||||
| 8х16 | -267.497 | 3.93130435 | -265.9636667 | -265.954683 | -265.9591749 | 0.004491743 | ||
| 16х32 | -266.347 | 3.97923875 | -265.9616667 | -265.960995 | -265.961331 | 0.000335656
| ||
| 32х64 | -266.058 | 4.01388889 | -265.962 | -265.962111 | -265.9620553 | 5.52995E-05 | ||
| 64х128 | -265.986 |
По столбцу 2 табл. 2 видно, что перемещение изменяется от -272.018 мм. до -265.986 мм. Если оценивать точность решения по близости результатов на последовательно сгущаемых сетках, то можно сделать вывод, что прогиб определен с точностью в 3 значащие цифры и равен -267 мм. По методу Шварцмана уже после первых трех расчетов мы получили прогиб -265.96 мм с точностью до 5 значащих цифр. Следовательно, уже первый результат метода Шварцмана дает решение, точность которого выше точности результата, полученного за 5 расчетов обычным способом.
Таблица 3
Оценка точности определения изгибающего момента 

|
|
|
|
|
|
|
| 4х8 | 5719.7 | |||||
| 8х16 | 6318.89 | 4.0278973 | 6517.236667 | 6516.779804 | 6517.008 | 0.22843135 |
| 16х32 | 6467.65 | 4.0064638 | 6517.156667 | 6517.130057 | 6517.143 | 0.01330467 |
| 32х64 | 6504.78 | 4.0010776 | 6517.153333 | 6517.152223 | 6517.153 | 0.00055536 |
| 64х128 | 6514.06 |
Так же в случае изгибающих моментов (табл. 3, 4) после трех расчетов метод Шварцмана дает точность результатов, превышающую таковую, полученную за 5 расчетов обычным способом. Полученные значения величин  являются окончательными значениями приближенных решений. Данная величина отличается от точного решения на величину е, которая в методе Шварцмана является оценкой погрешности соответствующего решения
являются окончательными значениями приближенных решений. Данная величина отличается от точного решения на величину е, которая в методе Шварцмана является оценкой погрешности соответствующего решения  :,
:,  , где
, где  - точное решение задачи.
- точное решение задачи.
Произведя расчеты, мы получаем не только приближенное решение  , но и его оценку. Таким образом, метод Шварцмана позволяет оценить погрешность решения.
, но и его оценку. Таким образом, метод Шварцмана позволяет оценить погрешность решения.
Таблица 4
Оценка точности определения изгибающего момента 

|
|
|
|
|
|
|
| 4х8 | 2187.38 | |||||
| 8х16 | 2406.62 | 3.8955224 | 2481.66 | 2482.336907 | 2481.998 | 0.33845361 |
| 16х32 | 2462.9 | 3.9717713 | 2481.793333 | 2481.8382 | 2481.816 | 0.02243331 |
| 32х64 | 2477.07 | 3.9915493 | 2481.803333 | 2481.806676 | 2481.805 | 0.00167137 |
| 64х128 | 2480.62 |
Алгоритм определения шага сетки, обеспечивающего заданную погрешность расчетов. Допустим, что необходимо найти приближенное значение  с заданной абсолютной погрешностью
с заданной абсолютной погрешностью  . Как найти шаг
. Как найти шаг  сетки, необходимый для проведения такого расчета?
сетки, необходимый для проведения такого расчета?
Пусть, выполнено решение задачи на трех последовательных сетках  ,
,  ,
,  . По полученным приближенным решениям
. По полученным приближенным решениям  ,
,  ,
,  вычислены величины
вычислены величины
 ,
,  . (6)
. (6)
Вводим обозначения
 ,
, 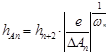 , (7)
, (7)
где  ,
,  – коэффициент сгущения сетки (в нашем случае равен 2).
– коэффициент сгущения сетки (в нашем случае равен 2).
В [3, 4] доказано: если  монотонно сходится к
монотонно сходится к  , то величины
, то величины  и
и  дают двусторонние оценки шага
дают двусторонние оценки шага  сетки, необходимой для получения решения с заданной погрешностью
сетки, необходимой для получения решения с заданной погрешностью  :
:
 . (8)
. (8)
Таким образом, по результатам нескольких расчетов на последовательно сгущающихся сетках формулы (7),(8) позволяют оценить шаг  сетки, который гарантирует получение приближенного решения с заданной погрешностью
сетки, который гарантирует получение приближенного решения с заданной погрешностью  .
.
Пример 2
2.1. Перемещение  . Рассмотрим пример, когда необходимо найти шаг
. Рассмотрим пример, когда необходимо найти шаг  сетки такой, чтобы обеспечить вычисление прогиба с заданной абсолютной погрешностью
сетки такой, чтобы обеспечить вычисление прогиба с заданной абсолютной погрешностью  . Обратимся к результатам примера 1 (табл. 2). На основе формул (6) вычисляем величины
. Обратимся к результатам примера 1 (табл. 2). На основе формул (6) вычисляем величины  и
и  .
.
 ,
,  .
.
Подсчитываем  . Далее на основе формул (7) рассчитываем
. Далее на основе формул (7) рассчитываем  и
и 
Таким образом, если мы хотим получить результат с абсолютной погрешностью в 1 мм, нам необходимо принять шаг разбиения сетки  .
.
2.2 Изгибающий момент  . За заданную абсолютную погрешность примем 10 кН·м.
. За заданную абсолютную погрешность примем 10 кН·м.
Обратимся к табл. 3. На основе формул (6) вычисляем величины  и
и  .
.
 ,
, 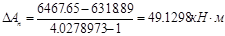
Подсчитываем  . Далее на основе формул (7) рассчитываем
. Далее на основе формул (7) рассчитываем  ,
, 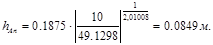
Таким образом, если мы хотим получить результат с абсолютной погрешностью в 10 кН∙м , нам необходимо принять шаг разбиения сетки 
2.3 Изгибающий момент  . За заданную абсолютную погрешность примем 10 кН·м.
. За заданную абсолютную погрешность примем 10 кН·м.
Обратимся к табл. 4. На основе формул (6) вычисляем величины  и
и  .
.
 ,
, 
Подсчитываем  .
.
Далее на основе формул (7) рассчитываем  ,
, 
Таким образом, если мы хотим получить результат с абсолютной погрешностью в 10 кН∙м, нам необходимо принять шаг разбиения сетки 
По результатам трех расчетов на последовательно сгущающихся сетках мы можем определить шаг сетки, который будет гарантировать получение приближенного решения с заданной погрешностью 
Заключение
1. Произведя серию расчетов, мы получаем приближенное решение. Метод Шварцмана позволяет, что очень важно, оценить погрешность этого решения.
2. Задавая необходимую точность расчета, можем определить шаг сетки, который будет гарантировать получение приближенного решения с заданной погрешностью 
Дата добавления: 2018-10-26; просмотров: 270; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!

 , мм.
, мм.