В чём состоит первая задача динамики?

1-я задача динамики (для материальной точки): зная закон движения точки определить действующую на нее силу.

В чём состоит вторая задача динамики?

2-я задача динамики (для материальной точки): зная действующую на точку силы, определить закон движения точки.

18 .

К мерам движения относят следующие характеристики их инертности и движения : количество движения (импульс) точки и системы, кинетический момент (момент количества движения ) точки и системы относительно точки и оси, кинетическую энергию точки и системы.

Количеством движением точки называют векторную величину, равную произведению массы точки на ее скорость

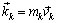Количеством движением механической системы называют сумму количеств движений всех ее точек

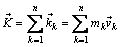Эту величину можно выразить и через скорость центра масс

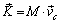Размерность количества движения – кг·м/с.

Кинетическим моментом или моментом количества движения материальной точки относительно некоторого центра О называют векторную величину 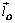, равную векторному произведению радиус-вектора точки 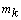, проведенного к ней из центра О, на вектор количества движения 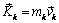этой точки

. (

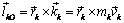Кинетическим моментом материальной точки относительно оси называют проекцию на эту ось, например, Oz, кинетического момента относительно любой точки на этой же оси

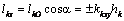Кинетическим моментом механической системы относительно точки или оси называют сумму кинетических моментов всех точек системы относительно точки

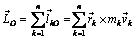
или оси, например, оси Ох

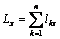. Кинетический момент тела вращения относительно его неподвижной оси, например, оси Oz, равен произведению момента инерции тела относительно этой оси на его угловую скорость

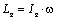Кинетической энергией материальной точки называют скалярную величину, равную половине произведения массы точки на квадрат ее скорости

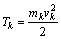Кинетической энергией механической системы материальных точек называют сумму кинетических энергий всех точек этой системы

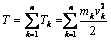Она равна нулю, если все точки системы в какой-то момент времени неподвижны.

Размерность кинетической энергии – Джоуль, 1 Дж = 1 Н∙м

14 (1)

19/

20.

Количество движения материальной точки - вектор, численно равный произведению массы точки на скорость ее движения и совпадающий с ней по направлению.

Векторная производная по времени от количества движения материальной точки геометрически равна вектору силы, действующей на точку.

Основное уравнение динамики: 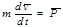; 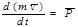. Интегрируя получим: ; .

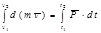Теорема: Изменение количества движения материальной точки за некоторый промежуток времени равно импульсу силы, действующей на точку за этот промежуток времени.

21.

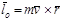; взяв производную по времени от обоих частей уравнения получим: 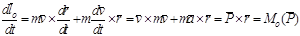, итак: .

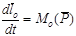Теорема: векторная производная по времени от момента количества движения материальной точки относительно полюса равна вектору момента силы, действующей на точку относительно того же центра.

Следствия:

1. если линия действия силы проходит через полюс. То момент количества движения относительно этого полюса постоянный;

2. если момент силы относительно оси равен нулю, то момент количества движения относительно этой оси постоянный.

22.

1) Работа силы тяжести. Пусть точка М, на которую действует сила тяжести 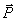, перемещается из положения М₀ ( x ₀, у₀, z ₀ ) в положение M ₁ (х₁, у₁, z ₁ ). Выберем оси координат так, чтобы ось Oz была направлена вертикально вверх (рис.19).

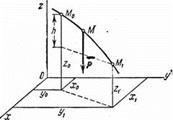
Рис.19

Тогда Р_x=0, Р_y=0, P_z= -Р. Подставляя эти значения и учитывая переменную интегрирования z :

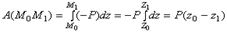Если точка M₀ выше М₁, то 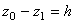, где h-величина вертикального перемещения точки;

Если же точка M₀ ниже точки M₁то .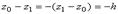

Окончательно получаем: .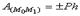

Следовательно, работа силы тяжести равна взятому со знаком плюс или минус произведению модуля силы на вертикальное перемещение точки ее приложения. Работа положительна, если начальная точка выше конечной, и отрицательна, если начальная точка ниже конечной. Из полученного результата следует, что работа силы тяжести не зависит от вида той траектории, по которой перемещается точка ее приложения.

Силы, обладающие таким свойством, называются потенциальными

23.Рассмотрим точку с массой т, перемещающуюся под действием приложенных к ней сил из положения M₀ , где она имеет скорость 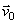, в положение М₁ , где ее скорость равна .

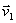Для получения искомой зависимости обратимся к уравнению 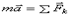выражающему основной закон динамики. Проектируя обе части этого равенства на касательную 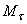к траектории точки М, направленную в сторону движения, получим:

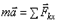Стоящую слева величину касательного ускорения можно представить в виде

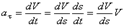В результате будем иметь:

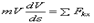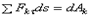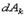.Умножив обе части этого равенства на ds , внесем т под знак дифференциала. Тогда, замечая, что где - элементарная работа силы F_k получим выражение теоремы об изменении кинетической энергии в дифференциальной форме:

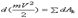.Проинтегрировав теперь обе части этого равенства в пределах, соответствующих значениям переменных в точках M₀ и M₁, найдем окончательно:

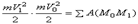Уравнение выражает теорему об изменении кинетической энергии точки в конечном виде: изменение кинетической энергии точки при некотором ее перемещении равно алгебраической сумме работ всех действующих на точку сил на том же перемещении.

24.

25.

Механической системой материальных точек или тел называется такая их совокупность, в которой положение или движение каждой точки (или тела) зависит от положения и движения всех остальных.

Внутренними называются силы, действующие на точки системы со стороны других точек или тел этой же системы. Будем обозначать внутренние - .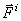

Внутренние силы обладают следующими свойствами:

1. Геометрическая сумма (главный вектор) всех внутренних сил системы равняется нулю. В самом деле, по третьему закону динамики любые две точки системы (рис.31) действуют друг на друга с равными по модулю и противоположно направленными силам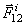и и 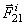, сумма которых равна нулю. Так как аналогичный результат имеет место для любой пары точек системы, то

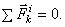
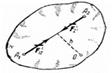
2. Сумма моментов (главный момент) всех внутренних сил системы относительно любого центра или оси равняется нулю. Действительно, если взять произвольный центр О, то из рис.18 видно, что 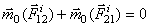. Аналогичный результат получится при вычислении моментов относительно оси. Следовательно, и для всей системы будет:

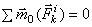или .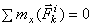

Из доказанных свойств не следует однако, что внутренние силы взаимно уравновешиваются и не влияют на движение системы, так как эти силы приложены к разным материальным точкам или телам и могут вызывать взаимные перемещения этих точек или тел. Уравновешенными внутренние силы будут тогда, когда рассматриваемая система представляет собою абсолютно твердое тело.

Дата добавления: 2018-10-26; просмотров: 148; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 34

Мы поможем в написании ваших работ!