Смешанное произведение трех векторов
Смешанным произведением трех векторов 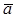 ,
, 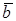 и
и  называется число, равное скалярному произведению вектора
называется число, равное скалярному произведению вектора 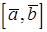 на вектор
на вектор 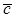 . Принято обозначение смешанного произведения трех векторов
. Принято обозначение смешанного произведения трех векторов  (или
(или  ).
).
Геометрические свойства смешанного произведения:
1 модуль смешанного произведения  равен объему параллелепипеда, построенного на векторах
равен объему параллелепипеда, построенного на векторах 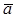 ,
, 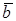 и
и 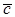 ;
;
2 векторы 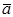 ,
, 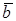 и
и 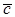 лежат в одной плоскости тогда и только тогда, когда
лежат в одной плоскости тогда и только тогда, когда  .
.
Если векторы 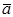 ,
, 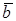 и
и 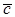 заданы декартовыми координатами:
заданы декартовыми координатами: 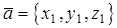 ,
,  ,
,  , то смешанное произведение вычисляется по формуле
, то смешанное произведение вычисляется по формуле
 .
.
Пример. Даны вершины тетраэдра  ,
,  ,
,  ,
,  . Найти длину высоты, опущенную из вершины
. Найти длину высоты, опущенную из вершины  .
.
Решение.
|
|

 .
.
Тогда 

Откуда получим  . Вычислим
. Вычислим  (см. предыдущий пример).
(см. предыдущий пример).

Тогда 
Кривые второго порядка
В декартовой системе координат общее уравнение кривой второго порядка имеет вид
 (2)
(2)
где не все коэффициенты  ,
, 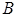 и
и  одновременно равны нулю. Если
одновременно равны нулю. Если  , то уравнение
, то уравнение  определяет прямую линию.
определяет прямую линию.
В декартовой системе координат уравнение (2) примет один из следующих видов:
1)  каноническое уравнение окружности с центром в точке
каноническое уравнение окружности с центром в точке  и радиусом
и радиусом  ;
;
2)  каноническое уравнение эллипса с центром в точке
каноническое уравнение эллипса с центром в точке  и полуосями
и полуосями  и
и  ;
;
3) канонические уравнения гиперболы:
а)  каноническое уравнение гиперболы с центром в точке
каноническое уравнение гиперболы с центром в точке  , действительной полуосью
, действительной полуосью  и мнимой полуосью
и мнимой полуосью  ;
;
б)  каноническое уравнение гиперболы с центром в точке
каноническое уравнение гиперболы с центром в точке  , действительной полуосью
, действительной полуосью  и мнимой полуосью
и мнимой полуосью 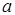 ;
;
|
|
|
4) канонические уравнения параболы:
а)  каноническое уравнение параболы с вершиной в точке
каноническое уравнение параболы с вершиной в точке  и осью симметрии, параллельной оси
и осью симметрии, параллельной оси  .
.
б)  каноническое уравнение параболы с вершиной в точке
каноническое уравнение параболы с вершиной в точке  и осью симметрии, параллельной оси
и осью симметрии, параллельной оси  .
.
Используя каноническое уравнение кривой, легко построить график данной линии в декартовой системе координат.
Пример. Привести уравнение кривой второго порядка  к каноническому виду. Определить вид кривой и построить ее график.
к каноническому виду. Определить вид кривой и построить ее график.
а) 



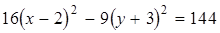 .
.
Разделим обе части уравнения на 144:  . Данное уравнение определяет гиперболу с центром в точке
. Данное уравнение определяет гиперболу с центром в точке  , действительной полуосью
, действительной полуосью  и мнимой полуосью
и мнимой полуосью  . Сделаем схематический чертеж.
. Сделаем схематический чертеж.

|
|
б) 




 парабола с вершиной в точке
парабола с вершиной в точке  и осью симметрии, параллельной оси
и осью симметрии, параллельной оси  .
.
в)  .
.
Преобразуем это уравнение, возведя обе части в квадрат
 ,
,  ,
,  ,
,  .
.
Последнее уравнение определяет эллипс с центром в точке 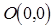 и полуосями
и полуосями  ,
,  . Если решить данное уравнение относительно
. Если решить данное уравнение относительно  , получим
, получим
 ,
,  .
.
|
В условии задачи дано второе из этих уравнений. Оно определяет не весь эллипс, а только ту его часть, для точек которой  , т.е. половину эллипса, расположенную ниже оси
, т.е. половину эллипса, расположенную ниже оси  .
.
|
|
|
ПРЯМАЯ ЛИНИЯ НА ПЛОСКОСТИ.
ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМЫХ
Всякое уравнение первой степени относительно  и
и  , т. е. уравнение вида
, т. е. уравнение вида
 , (6)
, (6)
где  ,
, 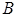 и
и  - постоянные коэффициенты, причем
- постоянные коэффициенты, причем  , определяет на плоскости некоторую прямую. Это уравнение называется общим уравнением прямой.
, определяет на плоскости некоторую прямую. Это уравнение называется общим уравнением прямой.
Если в общем уравнении прямой  , то разрешив его относительно
, то разрешив его относительно  , получим уравнение прямой с угловым коэффициентом
, получим уравнение прямой с угловым коэффициентом
 , (7)
, (7)
где  - тангенс угла, образованного прямой с положительным направлением оси
- тангенс угла, образованного прямой с положительным направлением оси  ;
;  - ордината точки пересечения прямой с осью
- ордината точки пересечения прямой с осью  .
.
Уравнение  (8)
(8)
является уравнением прямой, которая проходит через точку  и имеет угловой коэффициент
и имеет угловой коэффициент  .
.
Если в общем уравнении прямой  , то, разделив все члены на
, то, разделив все члены на 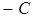 , получим уравнение прямой «в отрезках»
, получим уравнение прямой «в отрезках»
 , (9)
, (9)
где  ,
,  – величины направленных отрезков, отсекаемых прямой на осях координат
– величины направленных отрезков, отсекаемых прямой на осях координат  и
и  , соответственно.
, соответственно.
Уравнение
 , (10)
, (10)
|
|
|
является уравнением прямой, проходящей через две точки  и
и  .
.
Обозначим  ,
,  координаты направляющего вектора прямой
координаты направляющего вектора прямой  , тогда (10) примет вид
, тогда (10) примет вид
 , (11)
, (11)
где  – точка на прямой. Уравнение (11) называется каноническим уравнением прямой. Введя параметр
– точка на прямой. Уравнение (11) называется каноническим уравнением прямой. Введя параметр  , из (10) получим параметрические уравнения прямой
, из (10) получим параметрические уравнения прямой
 где
где  (12)
(12)
Уравнение прямой, проходящей через точку  перпендикулярно вектору
перпендикулярно вектору  , имеет вид
, имеет вид
 . (13)
. (13)
Вектор  – называется нормальным вектором прямой. Раскрывая в (13) скобки, получим общее уравнение прямой
– называется нормальным вектором прямой. Раскрывая в (13) скобки, получим общее уравнение прямой
 .
.
Таким образом, в общем уравнении прямой, коэффициенты при  и
и  суть координаты нормального вектора прямой.
суть координаты нормального вектора прямой.
Пусть две прямые заданы уравнениями с угловыми коэффициентами  и
и  . Возможны следующие случаи их взаимного расположения:
. Возможны следующие случаи их взаимного расположения:
1) прямые параллельны (в частности совпадают) тогда и только тогда, когда выполняется условие  ;
;
2) прямые пересекаются в некоторой точке, тогда угол между ними находится по формуле  ;
;
3) прямые перпендикулярны тогда и только тогда, когда  .
.
Пример. В равнобедренном прямоугольном треугольнике даны декартовы координаты вершины острого угла  и уравнение противолежащего катета
и уравнение противолежащего катета 
 . Составить уравнения двух других сторон этого треугольника.
. Составить уравнения двух других сторон этого треугольника.
|
|
|
Решение.
|
|
Найдем уравнение прилежащего катета. Так как  ,
, 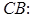
 , то уравнение
, то уравнение  имеет вид
имеет вид 

 .
.  Угол между катетом и гипотенузой в равнобедренном треугольнике
Угол между катетом и гипотенузой в равнобедренном треугольнике 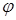 равен
равен  . Для нахождения уравнения гипотенузы воспользуемся формулой
. Для нахождения уравнения гипотенузы воспользуемся формулой  , из которой найдем угловой коэффициент прямой
, из которой найдем угловой коэффициент прямой  .
.
1.  .
.
Тогда уравнение  имеет вид
имеет вид





2.  .
.
Тогда уравнение 



Ответ: 
 ,
, 



Прямая и плоскость в пространстве
Плоскость в декартовой системе координат может быть задана следующими уравнениями:
1. Общее уравнение плоскости
 .
.
Кроме того,

уравнение плоскости, которая проходит через точку  перпендикулярно вектору
перпендикулярно вектору  .
.
2. Уравнение плоскости “в отрезках”
 ,
,
где 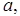

 – величины направленных отрезков, отсекаемых плоскостью на координатных осях
– величины направленных отрезков, отсекаемых плоскостью на координатных осях  ,
,  и
и  , соответственно.
, соответственно.
3. Уравнение плоскости, проходящей через три точки 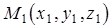 ,
,  ,
, 
 .
.
Прямая в пространстве задается:
1) общими уравнениями  в пространстве в
в пространстве в 

где  , таким образом, прямая задана как линия пересечения двух плоскостей.
, таким образом, прямая задана как линия пересечения двух плоскостей.
2) каноническими уравнениями  в
в 
 ,
,
где  – точка, принадлежащая прямой, а
– точка, принадлежащая прямой, а  – направляющий вектор.
– направляющий вектор.
3) параметрическими уравнениями

Пример. Составить уравнение плоскости, проходящей через точку  и прямую
и прямую 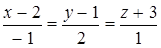 .
.
Решение.
Уравнение плоскости, проходящей через точку  и имеющей координаты вектора нормали
и имеющей координаты вектора нормали  , имеет вид
, имеет вид
 .
.
Найдем координаты вектора нормали.  – данная точка,
– данная точка,  – точка, лежащая на нашей прямой,
– точка, лежащая на нашей прямой,  – координаты направляющего вектора прямой. Тогда
– координаты направляющего вектора прямой. Тогда
 .
.
Запишем уравнение искомой плоскости
 ,
,
 ,
,

Дата добавления: 2018-09-23; просмотров: 231; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!




