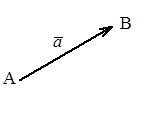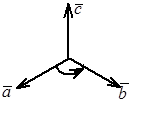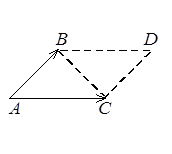Выберем в качестве базисного минора
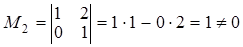 .
.
Следовательно, 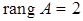 и система имеет ненулевые решения.
и система имеет ненулевые решения.
Запишем укороченную систему
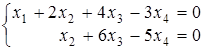 .
.
В качестве базисных неизвестных выберем 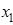 и
и 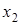 (т. к. в базисный минор выбраны 1-й и 2-й столбцы), тогда
(т. к. в базисный минор выбраны 1-й и 2-й столбцы), тогда 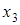 и
и 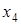 - свободные неизвестные. Полагая
- свободные неизвестные. Полагая 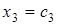 ,
, 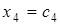 , находим
, находим 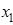 и
и 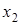 .
.
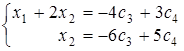 .
.
Подставим 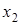 в первое уравнение системы и найдем
в первое уравнение системы и найдем 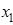 :
:
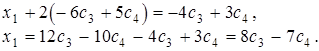
Запишем общее решение системы
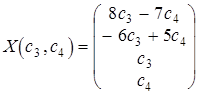 .
.
Из общего решения находим любое частное решение. Например, полагая 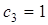 ,
, 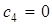 , получим
, получим 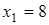 ,
, 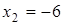 . Таким образом, частное решение системы имеет вид:
. Таким образом, частное решение системы имеет вид: 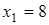 ,
, 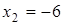 ,
, 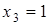 ,
, 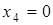 .
.
Варианты контрольных заданий для контрольной работы № 1
Элементы линейной алгебры
1. Найти значение матричного многочлена 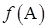 , если задан многочлен
, если задан многочлен 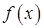 и матрица
и матрица 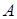
1.1. 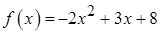 ,
, 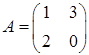 .
.
1.2. 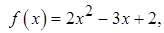
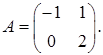
1.3. 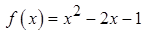 ,
, 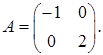
1.4. 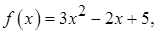
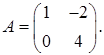
1.5. 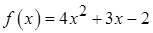 ,
, 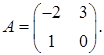
1.6. 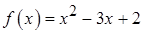 ,
, 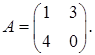
1.7.  ,
, 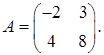
,
1.8. 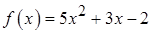 ,
, 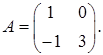
1.9. 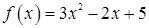 ,
, 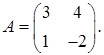
1.10. 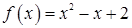 ,
, 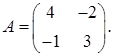
1.11. 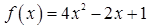 ,
, 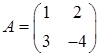 .
.
1.12. 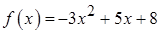 ,
, 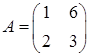 .
.
1.13. 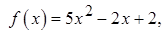
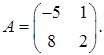
1.14. 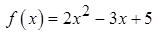 ,
, 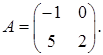
1.15. 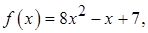
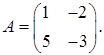
1.16. 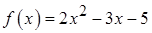 ,
, 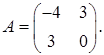
1.17. 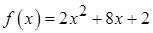 ,
, 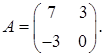
1.18. 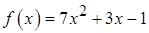 ,
, 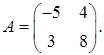
,
1.19. 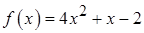 ,
, 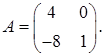
1.20. 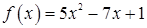 ,
, 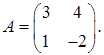
2. Найти произведение матриц 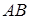 и
и 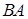 :
:
2.1 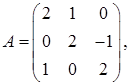
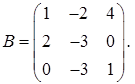
2.2. 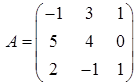 ,
, 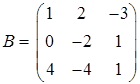 .
.
2.3. 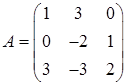 ,
, 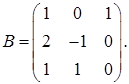
2.4. 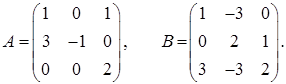
2.5. 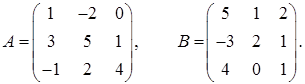
2.6. 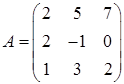 ,
, 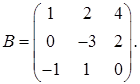
2.7. 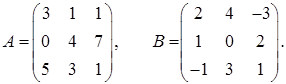
2.8. 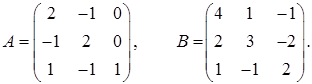
2.9. 
2.10. 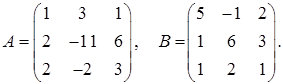
2.11. 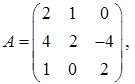
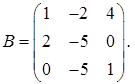
2.12. 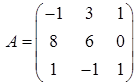 ,
, 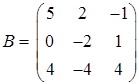 .
.
2.13. 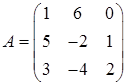 ,
, 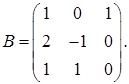
2.14. 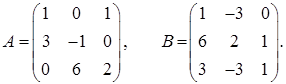
2.15. 
2.16. 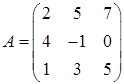 ,
, 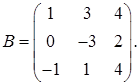
2.17. 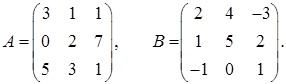
2.18. 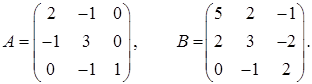
2.19. 
2.20. 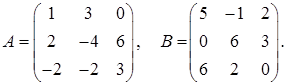
3. Вычислить определитель матрицы 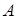 из задания 2, соответствующего варианта.
из задания 2, соответствующего варианта.
4. Доказать совместность системы линейных уравнений и решить ее двумя методами: 1) Крамера; 2) матричным.
4.1. 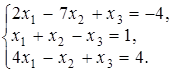 4.2.
4.2. 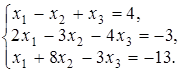
4.3. 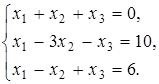 4.4.
4.4. 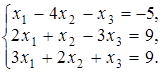
4.5. 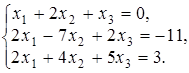 4.6.
4.6. 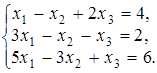
|
|
|
4.7. 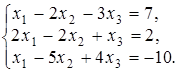 4.8.
4.8. 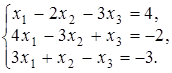
4.9. 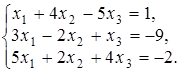 4.10.
4.10. 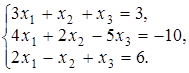
4.11. 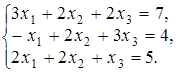 4.12.
4.12. 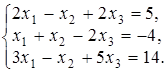
4.13. 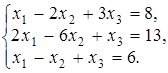 4.14.
4.14. 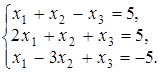
4.15. 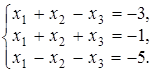 4.16.
4.16. 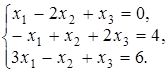
4.17.  4.18.
4.18. 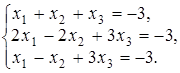
4.19. 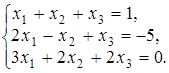 4.20.
4.20. 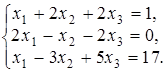
5. Найти общее и одно частное решение неоднородной системы линейных уравнений, записать фундаментальную систему решений.
5.1. 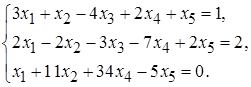 5.2.
5.2. 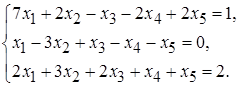
5.3. 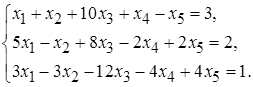 5.4.
5.4. 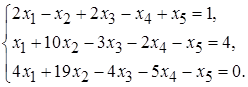
5.5.  5.6.
5.6. 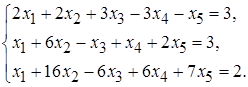
5.7. 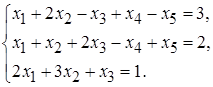 5.8.
5.8. 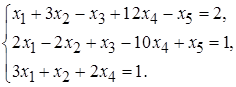
5.9. 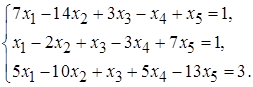 5.10.
5.10. 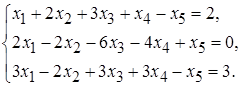
5.11. 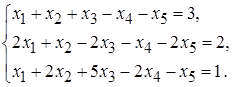 5.12.
5.12. 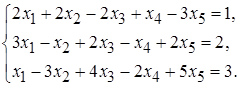
5.13. 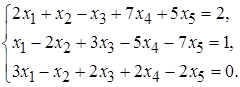 5.14.
5.14. 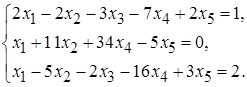
5.15. 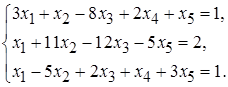 5.16.
5.16. 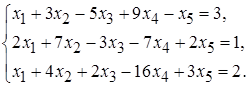
5.17. 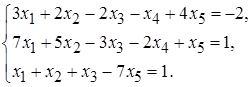 5.18.
5.18. 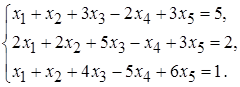
5.19. 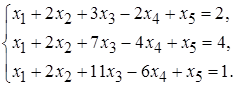 5.20.
5.20. 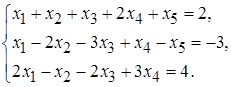
Методические указания к выполнению контрольной работы № 2
ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ
Понятие вектора. Линейные операции над векторами
Геометрическим вектором называется направленный отрезок. Обозначается вектор двумя большими латинскими буквами с общей чертой 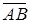 (
( 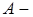 начало вектора,
начало вектора, 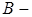 конец вектора) или одной малой
конец вектора) или одной малой 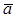 (см. рис.)
(см. рис.)
|
|
Векторы называются равными, если они имеют одинаковые длины, лежат на параллельных прямых или на одной прямой и направлены в одну сторону. Число, равное длине вектора, называется его модулем.
Если заданы декартовы координаты вектора 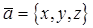 , то модуль вектора
, то модуль вектора 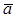 , обозначаемый символом
, обозначаемый символом 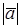 , вычисляется по формуле:
, вычисляется по формуле: 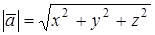 .
.
Если заданы две точки в декартовой системе координат 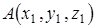 и
и 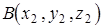 , где
, где 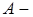 начало вектора,
начало вектора, 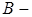 конец вектора, то координаты вектора
конец вектора, то координаты вектора 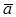 вычисляются по формулам
вычисляются по формулам 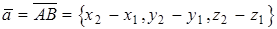 .
.
|
|
|
Операции алгебраического сложения векторов и умножение вектора на число называются линейными операциями над векторами.
1. Если 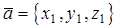 ,
, 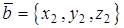 , то координаты вектора
, то координаты вектора 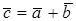 вычисляются по формулам
вычисляются по формулам 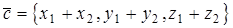 .
.
2. Если 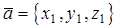 и
и 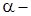 действительное число, то координаты вектора
действительное число, то координаты вектора 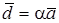 вычисляются по формулам
вычисляются по формулам 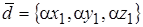 .
.
Пример. Даны два вектора 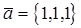 и
и 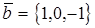 .
.
Вычислить а) 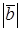 ; б)
; б)  .
.
Решение.
а) 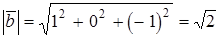 ;
;
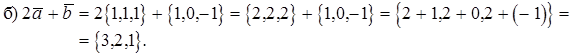
Скалярное произведение векторов, его свойства
Скалярным произведением двух векторов 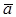 и
и 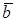 называется число, равное произведению модулей этих векторов на косинус угла между ними. Скалярное произведение векторов
называется число, равное произведению модулей этих векторов на косинус угла между ними. Скалярное произведение векторов 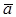 и
и 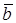 обозначается
обозначается 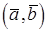 или
или 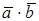 .
.
Обозначим через 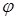 угол между векторами
угол между векторами 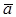 и
и 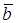 . Тогда скалярное произведение выражается формулой
. Тогда скалярное произведение выражается формулой
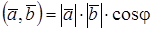 .
.
Если векторы 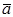 и
и 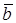 заданы декартовыми координатами
заданы декартовыми координатами 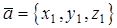 ,
, 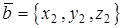 , то скалярное произведение вычисляется по формуле
, то скалярное произведение вычисляется по формуле
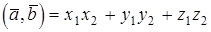 .
.
Скалярное произведение векторов 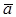 и
и 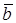 равно нулю (
равно нулю ( 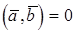 ) тогда и только тогда, когда векторы
) тогда и только тогда, когда векторы 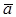 и
и 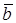 перпендикулярны. В частности
перпендикулярны. В частности 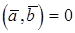 , если
, если 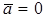 или
или 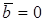 .
.
Алгебраические свойства скалярного произведения:
1. 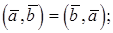
2. 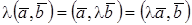 , где
, где 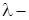 константа;
константа;
3. 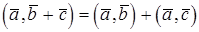 .
.
С помощью скалярного произведения можно вычислить:
|
|
|
1. Модуль вектора 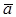 :
: 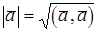 . Эта формула справедлива для любой системы координат. В частности, в декартовой системе координат данная формула примет вид
. Эта формула справедлива для любой системы координат. В частности, в декартовой системе координат данная формула примет вид 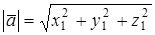 , где
, где 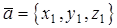 .
.
2. Косинус угла между векторами 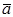 и
и 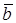
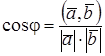 .
.
3. Проекцию вектора 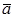 на вектор
на вектор 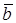
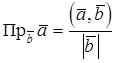 .
.
Пример. Векторы 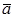 и
и 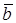 взаимно перпендикулярны и
взаимно перпендикулярны и 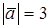 ,
, 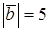 . Найти
. Найти 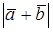 .
.
Решение.
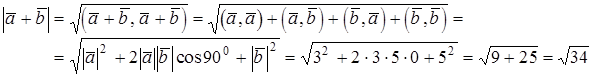 .
.
Пример. Вычислить косинус угла, образованного векторами 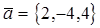 и
и 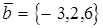 .
.
Решение.
Воспользуемся формулой 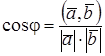 .
.
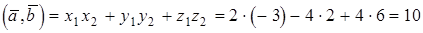 ;
;
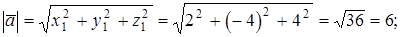
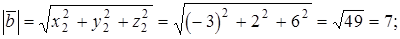
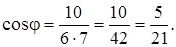
Векторное произведение векторов
Векторным произведением вектора 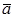 на вектор
на вектор 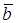 называется вектор
называется вектор 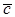 , обозначаемый символом
, обозначаемый символом 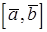 (или
(или 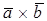 ) и определяемый тремя правилами:
) и определяемый тремя правилами:
1. 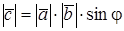 , где
, где 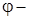 угол между векторами
угол между векторами 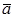 и
и 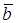 ;
;
2. вектор 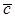 перпендикулярен к каждому из векторов
перпендикулярен к каждому из векторов 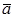 и
и 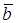 ;
;
|
|
3. вектор 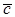 ориентирован так, что если смотреть с его конца на плоскость векторов
ориентирован так, что если смотреть с его конца на плоскость векторов 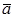 и
и 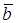 , то кратчайший поворот от
, то кратчайший поворот от 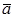 к
к 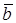 происходит против часовой стрелки (см. рис.)
происходит против часовой стрелки (см. рис.)
Алгебраические свойства векторного произведения:
1) 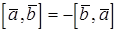 ;
;
2) 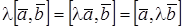 , где
, где 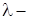 вещественное число;
вещественное число;
3) 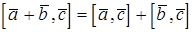 .
.
Геометрические свойства векторного произведения:
1) модуль векторного произведения 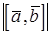 равен площади параллелограмма, построенного на векторах
равен площади параллелограмма, построенного на векторах 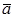 и
и 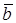 ;
;
2) если 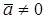 ,
, 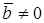 , то
, то 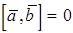 тогда и только тогда, когда
тогда и только тогда, когда 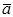 и
и 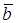 параллельные векторы;
параллельные векторы;
|
|
|
3) если векторы 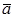 и
и 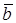 заданы декартовыми координатами
заданы декартовыми координатами 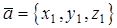 ,
, 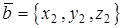 , то векторное произведение
, то векторное произведение 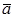 на
на 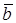 вычисляется по формуле
вычисляется по формуле
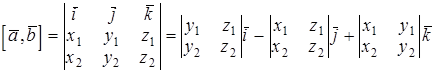 .
.
Пример. Даны точки 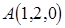 ,
, 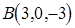 ,
, 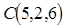 . Вычислить площадь треугольника
. Вычислить площадь треугольника 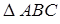 .
.
Решение.
|
|
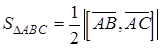 ,
, 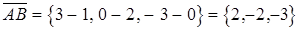
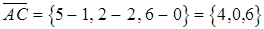
Вычислим 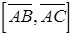 :
:
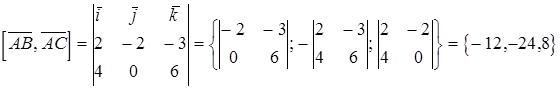
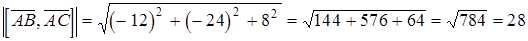 .
.
Тогда 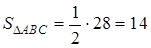 (кв.ед.).
(кв.ед.).
Дата добавления: 2018-09-23; просмотров: 178; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!