Метод градиентного спуска с дроблением шага
Метод градиентного спуска является одним из самых распространенных и самых простых методов решения задачи безусловной оптимизации. Он основан на свойстве градиента функции, согласно которому направление градиента совпадает с направлением наискорейшего возрастания функции, а направление антиградиента – с направлением наискорейшего убывания функции. При решении задачи безусловной минимизации за направление спуска из точки x ( m ) выбирается p(m) = –g(x(m)) = –f '(x(m)). Таким образом, итерационная процедура (2.20) для этого метода имеет вид
x(m+1) = x(m) – a(m)g(x(m)). (2.24)
Для выбора шага a(m) можно использовать процедуру дробления шага, которая состоит в следующем. Произвольно фиксируют начальное значение шага a(m) = a(m – 1) = a. Если в точке x(m+1), вычисленной в соответствии с (2.24), выполняется неравенство
f(x(m+1)) > f(x(m)),
то шаг дробится, например, пополам, т.е. полагается a(m +1) = 0.5a(m ).
Применим метод градиентного спуска с дроблением шага для минимизации квадратичной функции
f(x) = 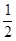 (Ax , x) + (b, x) + c
(Ax , x) + (b, x) + c
с симметричной положительно определенной матрицей A .
Алгоритм 2.1 (Алгоритм метода градиентного спуска с дроблением шага для квадратичной функции).
Шаг 1. Для квадратичной функции f(x) = 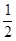
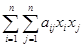 +
+ 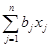 + с ввести матрицу A =(aij), вектор b = (b1, b2, … , bn)T и коэффициент c , i = 1, … , n; j = 1, … , n. Выбрать произвольную начальную точку x = (x1, x2, … , xn)T, например, x = (0, 0, … , 0)T, начальный шаг a и погрешность вычислений e > 0. Вычислить f ( x ).
+ с ввести матрицу A =(aij), вектор b = (b1, b2, … , bn)T и коэффициент c , i = 1, … , n; j = 1, … , n. Выбрать произвольную начальную точку x = (x1, x2, … , xn)T, например, x = (0, 0, … , 0)T, начальный шаг a и погрешность вычислений e > 0. Вычислить f ( x ).
|
|
|
Шаг 2. Вычислить g = f '(x) = Ax + b, или покоординатно
g = (g1, g2, … , gn)T,
gi = 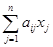 + bi, i = 1, …, n.
+ bi, i = 1, …, n.
Шаг 3. Для заданной точности вычислений e проверить выполнение критерия окончания вычислений.: ||f '(x)|| < e , Если это условие выполнено, вычисления закончить и за приближенное значение точки минимума принять точку x* = x = (x1, x2, … , xn)T. В противном случае перейти к шагу 4 для продолжения итерационного процесса.
Шаг 4. Вычислить
y = (y1, y2, … , yn),
yi= xi– a gi, i = 1, …, n.
Шаг 5. Вычислить f(y).
Шаг 6. Если f(y) < f(x), то положить x = y , f(x) = f(y) и перейти к шагу 2, иначе – перейти к шагу 7.
Шаг 7. Положить a = 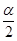 и перейти к шагу 4.
и перейти к шагу 4.
Пример 2.3.
Найдем минимум функции f(x) = x 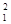 + 2x
+ 2x 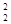 – 4x1 – 4x2 с точностью e = 0.01.
– 4x1 – 4x2 с точностью e = 0.01.
Матрица этой квадратичной функции имеет вид:
2 0
A= 0 4 , b = (– 4, – 4)T.
Критерий Сильвестра для функции f(x) выполнен:
D1 = 2 > 0, D2 = 2 × 4 – 0 × 0 = 8 > 0.
Следовательно, функция f(x) имеет минимум.
Возьмем начальное приближение x(0) =(x 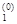 , x
, x 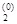 )T = (0, 0)T, положим e = 0.01 и будем вести вычисления в соответствии с алгоритмом 2. 1.
)T = (0, 0)T, положим e = 0.01 и будем вести вычисления в соответствии с алгоритмом 2. 1.
Шаг 1. Полагаем x = (0, 0)T, начальный шаг a = 0.6 и погрешность вычислений e =0.01. Вычисляем f(x) = 0.
Шаг 2. Вычисляем g = f '( x ) = Ax + b, или покоординатно
|
|
|
g = (g1, g2)T,
g1 = 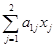 – b1 = 2×0 + 0×0 – 4 = –4,
– b1 = 2×0 + 0×0 – 4 = –4,
g2 = 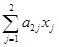 – b2 = 0×0 + 4×0 – 4 = –4,
– b2 = 0×0 + 4×0 – 4 = –4,
Шаг 3. Проверяем выполнение критерия окончания вычислений.
||f '(x)|| = 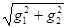 =
= 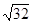 > e. Переходим к шагу 4.
> e. Переходим к шагу 4.
Шаг 4. Вычисляем
y = (y1, y2)
y1= x1 – a g1 = 0 – 0.6×(–4) = 2.4.
y2= x2 – a g2 = 0 – 0.6×(–4) = 2.4.
Шаг 5. Вычисляем f(y) = y 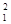 + 2y
+ 2y 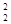 – 4y1 – 4y2 = –1.920.
– 4y1 – 4y2 = –1.920.
Шаг 6. Так как f(y) < f(x), то полагаем x = y = (2.4, 2.4)T , f(x) = f(y) = –1.920 и переходим к шагу 2.
Результаты последующих итераций приведены в табл. 2.1.
Таблица 2.1
| N | a | x1 | x2 | g1 | g2 | f(x) |
| 1 2 3 4 5 6 7 8 | 0.6 0.6 0.6 0.3 0.3 0.3 0.3 0.3 | 0 2.4 1.920 1.968 1.987 1.995 1.998 1.999 | 0 2.4 -0.960 1.392 1.022 1.016 0.997 1.001 | -4 0.8 -0.160 -0.064 -0.026 -0.010 -0.004 -0.002 | -4 5.600 -7.840 1.568 -0.324 0.063 -0.013 0.003 | 0 -1.920 1.690 -5.692 -5.988 -5.999 -6.000 -6.000 |
Из табл. 2.1 видно, что на третьей итерации значение функции возросло по сравнению с предыдущим. Поэтому значение шага стало в два раза меньше, a = 0.3.
Вычисления прекращаются после 8-ой итерации, так как требуемая точность достигнута (||f '(x)|| = 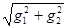 » 0.004 < 0.01).
» 0.004 < 0.01).
Таким образом, x* » (1.999, 1.001)T и f(x*) » –6.000.
Нетрудно убедиться, что существует точное значение точки минимума: x* = (2, 1)T и f(x*) = 6.
|
|
|
Метод наискорейшего спуска
В методе наискорейшего спуска величина шага a(m)из (2.24) находится в результате решения задачи одномерной минимизации
j(m)(a) = f(x(m) – a g(x(m))) ® min, a > 0. (2.25)
На рис. 2.3 изображена геометрическая иллюстрация этого метода. Из начальной точки x(0) перпендикулярно линии уровня f (x) = f (x(0)) в направлении p(0) = –g(0) спуск продолжают до тех пор, пока не будет достигнуто минимальное вдоль луча x(0) – a g(0) значение функции f. В найденной точке x(1) этот луч касается линии уровня f(x) = f(x(1)). Затем из точки x(1) проводят спуск в перпендикулярном линии уровня направлении p(1) = –g(1) до тех пор, пока соответствующий луч не коснется в точке x(2) проходящей через эту точку линии уровня и т. д.
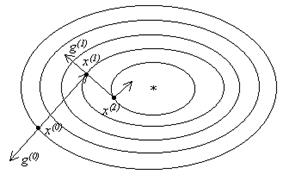
Рис. 2.3
Для квадратичной функции f(x) = 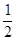 (Ax , x) + (b, x) + c с симметричной положительно определенной матрицей A эту задачу можно решить аналитически. Величина шага a(m), удовлетворяющая условию (2.25), равна (см., например, в [1])
(Ax , x) + (b, x) + c с симметричной положительно определенной матрицей A эту задачу можно решить аналитически. Величина шага a(m), удовлетворяющая условию (2.25), равна (см., например, в [1])
a(m) = 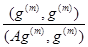 (2.26)
(2.26)
Опишем алгоритм метода наискорейшего спуска для квадратичной функции.
Алгоритм 2.2 (Алгоритм метода наискорейшего спуска для квадратичной функции).
|
|
|
Шаг 1. Для квадратичной функции f(x) = 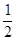
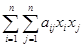 +
+ 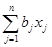 + с ввести матрицу A =(aij), вектор b = (b1, b2, … , bn)T и коэффициент c , i = 1, … , n; j = 1, … , n . Выбрать произвольную начальную точку x = (x1, x2, … , xn)T, например, x = (0, 0, … , 0)T и погрешность вычислений e > 0.
+ с ввести матрицу A =(aij), вектор b = (b1, b2, … , bn)T и коэффициент c , i = 1, … , n; j = 1, … , n . Выбрать произвольную начальную точку x = (x1, x2, … , xn)T, например, x = (0, 0, … , 0)T и погрешность вычислений e > 0.
Шаг 2. Вычислить g = f '( x ) = Ax + b, или покоординатно
g = (g1, g2, … , gn)T,
gi = 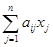 + bi, i = 1, …, n.
+ bi, i = 1, …, n.
Шаг 3. Для заданной точности вычислений e проверить выполнение критерия окончания вычислений.: ||f '(x)|| < e , Если это условие выполнено, вычисления закончить и за приближенное значение точки минимума принять точку x* = x = (x1, x2, … , xn)T, f* = f(x*).
В противном случае перейти к шагу 4 для продолжения итерационного процесса.
Шаг 4. (Шаги 4 – 7 используются для вычисления величины шага a(m)по формуле (2.26)
Вычислить
B1= (g, g) = 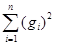 .
.
Шаг 5. Вычислить
Ag = (A1, A2, … , An)T, где
Ai = 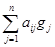 , i = 1, …, n.
, i = 1, …, n.
Шаг 6. Вычислить
B2 = (Ag, g) = 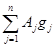 .
.
Шаг 7. Вычислить
a = 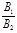 .
.
Шаг 8. Положить
x = x – a g(x)или покоординатно xi = xi – a gi, i = 1, …, n. Перейти к шагу 2.
Пример 2.4.
Как и в примере 2.3, найдем минимум функции f(x) = x 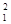 + 2x
+ 2x 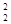 – 4x1 – 4x2 с точностью e = 0.01. В примере 2.3. было установлено, что функция f(x) имеет минимум. Найдем этот минимум методом наискорейшего спуска.
– 4x1 – 4x2 с точностью e = 0.01. В примере 2.3. было установлено, что функция f(x) имеет минимум. Найдем этот минимум методом наискорейшего спуска.
Шаги 1 – 3 совпадают с шагами 1 – 3 примера 2.3.
Шаг 1. Полагаем x = (0, 0)T и погрешность вычислений e =0.01. Вычисляем f(x) = 0.
Шаг 2. Вычисляем g = f '( x ) = Ax + b, или покоординатно
g = (g1, g2)T,
g1 = 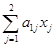 + b1 = 2×0 + 0×0 – 4 = –4,
+ b1 = 2×0 + 0×0 – 4 = –4,
g2 = 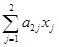 + b2 = 0×0 + 4×0 – 4 = –4.
+ b2 = 0×0 + 4×0 – 4 = –4.
Шаг 3. Проверяем выполнение критерия окончания вычислений.
||f '(x)|| = 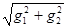 =
= 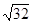 > e. Переходим к шагу 4.
> e. Переходим к шагу 4.
Шаг 4. Вычисляем
B1= (g, g) = 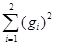 = 32.
= 32.
Шаг 5. Вычисляем
Ag = (A1, A2)T, где
A1 = 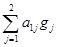 = 2×(–4) + 0×(–4) = –8,
= 2×(–4) + 0×(–4) = –8,
A2 = 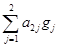 = 0×(–4) + 4×(–4) = –16.
= 0×(–4) + 4×(–4) = –16.
Шаг 6. Вычисляем
B2 = (Ag, g) = 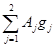 = (–8)×(–4) + (–16)×(–4) = 96.
= (–8)×(–4) + (–16)×(–4) = 96.
Шаг 7. Вычисляем
a = 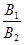 =
= 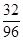 =
= 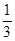 .
.
Шаг 8. Полагаем
x1 = x1– a g1 = 0 – 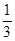 ×(–4) =
×(–4) = 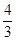 ,
,
x2 = x2 – a g2 = 0 – 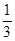 ×(–4) =
×(–4) = 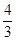 .
.
Перейдем к шагу 2 для следующей итерации.
Результаты последующих итераций приведены в табл. 2.2.
Таблица 2.2
| N | a | x1 | x2 | g1 | g2 | f(x) |
| 1 2 3 4 5 6 7 | 0.333 0.333 0.333 0.333 0.333 0.333 0.333 | 0 1.333 1.778 1.926 1.975 1.982 1.997 | 0 1.333 0.889 1.037 0.988 1.004 0.999 | -4 -1.333 -0.444 -0.148 -0.049 -0.016 -0.005 | -4 1.333 -0.444 0.148 -0.049 0.016 -0.005 | 0 -5.333 -5.926 -5.992 -5.999 -6.000 -6.000 |
Вычисления прекращаются после 7-ой итерации, так как требуемая точность достигнута (||f '(x)|| = 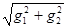 » 0.002 < 0.01).
» 0.002 < 0.01).
Таким образом, x* » (1.997, 0.999)T и f(x*) » –6.000.
Можно показать, что на m-ой итерации, m > 1, будут получены значения:
g(m) = 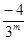 (1, (–1)m)T, a(m) =
(1, (–1)m)T, a(m) = 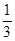 , x(m) = x* –
, x(m) = x* – 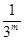 (2, (–1)m)T.
(2, (–1)m)T.
Существует точное значение точки минимума: x* = (2, 1)T.
Метод сопряженных градиентов
До сих пор в итерационной процедуре градиентного спуска
x(m+1) = x(m) + a(m)p ( m )
мы предполагали, что движение к минимуму функции производится в направлении антиградиента, p ( m ) = –g ( m ) . Для некоторых функций направление антиградиента в точке x(m) может значительно отличаться от направления к точке минимума x*. В результате траектория приближения к точке минимума может иметь зигзагообразный характер. Метод сопряженных градиентов в существенной степени избавлен от этого недостатка. Этот метод основан на понятии сопряженных направлений. Будем рассматривать задачу минимизации квадратичной функции
f(x) = 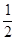 (Ax , x) + (b, x) + c
(Ax , x) + (b, x) + c
с симметричной положительно определенной матрицей A .
Направления p(0), p(1), … , p(m –1) называются взаимно сопряженными относительно матрицы A, если (Ap(k), p(l)) = 0 для всех k ¹ l.
В основе метода сопряженных градиентов лежит итерационный процесс:
x(m+1) = x(m) + a(m)p(m), m = 0, 1, …; p(0) = –g(0) = –f '(x(0)) .
Величина шага a(m) так же, как и в методе наискорейшего спуска, выбирается из условия одномерной минимизации функции j(m)(a) = f(x(m) + a(m)p(m)),
Направления p(m) находят по следующему правилу:
p(0) = –g(0) = –f '(x(0)),
p(m+1) = –g(m+1) + b(m) p(m), n ³ 1,
b(m) = 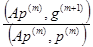 ,
,
g(m) = Ax(m) + b,
где
p(m) = p ( x(m)) – вектор сопряженных направлений;
g(m) = g(x(m)) – вектор направлений градиента;
x(m) = (x 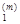 , x
, x 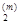 , … , x
, … , x 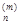 ) – m-ое приближение.
) – m-ое приближение.
Алгоритм 2.3 (Алгоритм метода сопряженных градиентов для квадратичной фун кции).
Шаг 1. Для квадратичной функции f(x) = 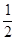
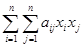 +
+ 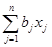 +с ввести матрицу A =(aij), вектор b = (b1, b2, … , bn)T и коэффициент c , i = 1, … , n; j = 1, … , n, Выбрать произвольную начальную точку x(0) = (x
+с ввести матрицу A =(aij), вектор b = (b1, b2, … , bn)T и коэффициент c , i = 1, … , n; j = 1, … , n, Выбрать произвольную начальную точку x(0) = (x 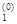 , x
, x 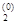 , … , x
, … , x 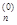 )T, например, x(0) = (0, 0, … , 0)T и погрешность вычислений e > 0.
)T, например, x(0) = (0, 0, … , 0)T и погрешность вычислений e > 0.
Шаг 2. Вычислить
p(0) = – g(0) = –(Ax(0) + b),
Покоординатно:
p(0) = (p 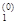 , p
, p 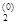 , … , p
, … , p 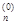 )T,
)T,
p 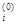 = – g
= – g 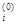 = –
= – 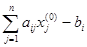 , i = 1, …, n.
, i = 1, …, n.
Далее вычисления производятся в цикле по m = 0, 1, … до тех пор, пока не будет выполнен критерий окончания вычислений.
Шаги 3 – 6 реализуют вычисление величины шага a(m)
Шаг 3. Вычислить
B 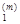 = (g(m), p(m)) =
= (g(m), p(m)) = 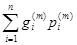 .
.
Шаг 4. Вычислить
Ap(m) = (A 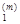 , A
, A 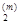 , … , A
, … , A 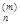 )T, где
)T, где
A 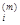 =
= 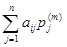 , i = 1, …, n.
, i = 1, …, n.
Шаг 5. Вычислить
B 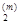 = (Ap(m), p(m)) =
= (Ap(m), p(m)) = 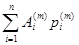 .
.
Шаг 6. Вычислить
a(m) = – 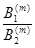 .
.
Шаг 7. Вычислить
x(m+1) = x(m) +a(m)p(m), или покоординатно
x(m+1) = (x 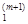 , x
, x 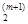 , … , x
, … , x 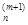 )T,
)T,
x 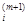 = x
= x 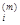 + a(m)p
+ a(m)p 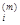 , i = 1, …, n.
, i = 1, …, n.
Шаг 8. Вычислить
g(m+1) = Ax(m +1) + b, или покоординатно
g(m+1) = (g 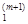 , g
, g 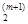 , … , g
, … , g 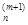 ),
),
g 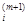 =
= 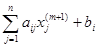 , i = 1, …, n.
, i = 1, …, n.
Шаг 9. Для заданной точности вычислений e проверить выполнение критерия окончания вычислений.: ||f '(x(m+1))|| = ||g(m+1))|| < e , Если это условие выполнено, вычисления закончить и за приближенное значение точки минимума принять точку x* = x(m+1) = (x 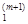 , x
, x 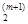 , … , x
, … , x 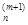 )T, f* = f(x*). В противном случае перейти к шагу 10 для продолжения итерационного процесса.
)T, f* = f(x*). В противном случае перейти к шагу 10 для продолжения итерационного процесса.
Шаги 10 – 12 реализуют вычисление нового вектора сопряженного градиента p(m+1).
Шаг 10. Вычислить
С 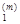 = (Ap(m), g(m+1)) =
= (Ap(m), g(m+1)) = 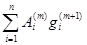 .
.
Шаг 11. Вычислить
b ( m ) = 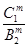 .
.
Шаг 12. Вычислить
p(m+1) = – g(m+1) + b ( m ) p(m), или покоординатно
p(m+1) = (p 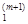 , p
, p 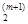 , … , p
, … , p 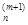 ),
),
p 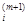 = – g
= – g 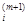 + b (m) p
+ b (m) p 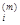 , i = 1, …, n.
, i = 1, …, n.
Шаг 13. Перейти к шагу 3 при m = m+1.
Пример 2.5.
Найдем минимум функции f(x) = x 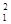 + 2x
+ 2x 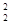 – 4x1 – 4x2 с точностью e = 0.1.
– 4x1 – 4x2 с точностью e = 0.1.
Как было показано ранее, эта функция имеет минимум в точке x* = (2, 1)T.
Матрица этой квадратичной функции имеет вид:
2 0
A= 0 4 , b = (– 4, – 4)T.
Применим метод сопряженных градиентов.
Шаг 1. Возьмем начальное приближение x(0) =(x 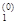 , x
, x 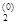 )T = (0, 0)T, положим e = 0.01.
)T = (0, 0)T, положим e = 0.01.
Шаг 2. Вычисляем
g(0) = (g 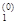 , g
, g 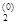 )T,
)T,
g 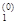 =
= 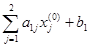 = 2×0 + 0×0 – 4 = –4,
= 2×0 + 0×0 – 4 = –4,
g 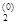 =
= 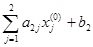 = 0×0 + 4×0 – 4 = –4,
= 0×0 + 4×0 – 4 = –4,
g(0) = (–4, –4) T,
p(0) = (p 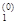 , p
, p 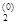 )T = (4, 4) T,
)T = (4, 4) T,
1- ая итерация, m = 0.
Шаг 3.
B 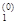 = (g(0), p(0)) = – (g(0), g(0)) = –
= (g(0), p(0)) = – (g(0), g(0)) = – 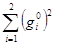 = –(16 + 16) = –32.
= –(16 + 16) = –32.
Шаг 4.
Ap(0) = (A 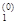 , A
, A 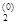 ),
),
A 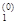 =
= 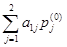 = 2×4 + 0×4 = 8,
= 2×4 + 0×4 = 8,
A 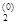 =
= 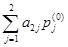 = 0×4 + 4×4 = 16.
= 0×4 + 4×4 = 16.
Шаг 5.
B 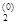 = (Ap(0), p(0)) =
= (Ap(0), p(0)) = 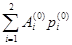 = 8×4 + 16×4 = 96.
= 8×4 + 16×4 = 96.
Шаг 6.
a (0) = – 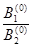 = –
= – 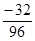 =
= 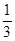 .
.
Шаг 7.
x(1) = x(0) +a (0) p(0),
x(1) = (x 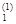 , x
, x 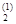 ),
),
x 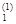 = x
= x 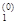 + a (0) p
+ a (0) p 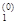 = 0 +
= 0 + 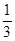 ×4 =
×4 = 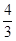 ,
,
x 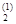 = x
= x 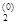 + a (0) p
+ a (0) p 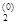 = 0 +
= 0 + 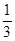 ×4 =
×4 = 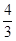 .
.
Шаг 8.
g(1) = Ax(1) + b, или покоординатно
g(1) = (g 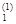 , g
, g 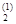 )T,
)T,
g 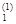 =
= 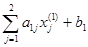 = 2×
= 2× 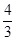 + 0×
+ 0× 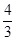 – 4 = –
– 4 = – 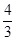 ,
,
g 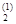 =
= 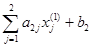 = 0×
= 0× 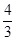 + 4×
+ 4× 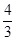 – 4 =
– 4 = 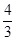 .
.
Шаг 9. Проверяем выполнение критерия окончания вычислений.:
||f '(x(1))|| = ||g(1))|| = 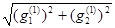 =
= 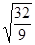 > e .
> e .
Переходим к шагу 10.
Шаг 10.
С 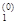 = (Ap(0), g(1)) =
= (Ap(0), g(1)) = 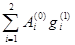 = 8×(–
= 8×(– 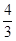 ) + 16×
) + 16× 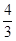 =
= 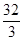 .
.
Шаг 11.
b (0) = 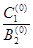 =
= 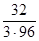 =
= 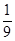 ×.
×.
Шаг 12. Определяем новое направление
p(1) = – g(1) + b (0) p(0), или покоординатно
p(1) = (p 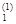 , p
, p 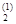 ),
),
p 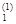 = – g
= – g 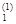 + b (0)p
+ b (0)p 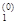 =
= 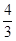 +
+ 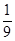 ×4 =
×4 = 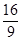 ,
,
p 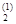 = – g
= – g 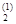 + b (0)p
+ b (0)p 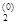 = –
= – 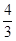 +
+ 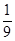 ×4 = –
×4 = – 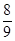 .
.
Шаг 13. Перейдем к шагу 3 при m = 1. Начало новой итерации.
2- ая итерация, m = 1.
Шаг 3.
B 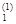 = (g(1), p(1)) =
= (g(1), p(1)) = 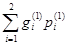 = –
= – 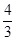 ×
× 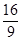 +
+ 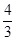 ×( –
×( – 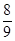 ) = –
) = – 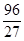 .
.
Шаг 4.
Ap(1) = (A 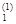 , A
, A 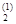 ),
),
A 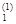 =
= 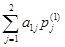 = 2×
= 2× 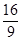 + 0×( –
+ 0×( – 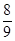 ) =
) = 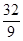 ,
,
A 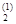 =
= 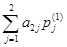 = 0×
= 0× 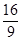 + 4×( –
+ 4×( – 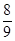 ) = –
) = – 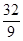 .
.
Шаг 5.
B 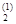 = (Ap(1), p(1)) =
= (Ap(1), p(1)) = 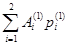 =
= 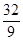 ×
× 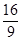 –
– 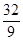 ×( –
×( – 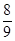 ) =
) = 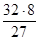 .
.
Шаг 6.
a (1) = – 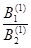 =
= 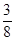 .
.
Шаг 7.
x(2) = x(1) +a(1) p(1),
x(2) = (x 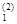 , x
, x 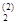 ),
),
x 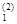 = x
= x 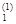 + a(1)p
+ a(1)p 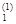 =
= 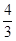 +
+ 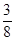 ×
× 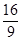 = 2,
= 2,
x 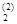 = x
= x 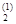 + a(1)p
+ a(1)p 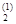 =
= 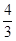 +
+ 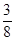 ×( –
×( – 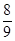 ) = 1.
) = 1.
Шаг 8.
g(2) = Ax(2) + b, или покоординатно
g(2) = (g 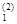 , g
, g 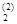 )T,
)T,
g 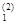 =
= 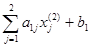 = 2×2+ 0×1 – 4 = 0,
= 2×2+ 0×1 – 4 = 0,
g 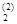 =
= 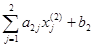 = 0×2+ 4×1 – 4 = 0.
= 0×2+ 4×1 – 4 = 0.
Шаг 9. Проверяем выполнение критерия окончания вычислений.:
||f '(x(2))|| = ||g(2))|| = 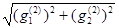 = 0 < e .
= 0 < e .
Вычисления прекращаем, так как требуемая точность достигнута.
Таким образом, полученное значение точки минимума x* равно точному значению x* = (2, 1)T и f(x*) » –6.000.
Решение найдено за два шага.
Метод покоординатного спуска
Пусть нужно найти минимум функции f(x1, x2, … ,xn). Основная идея метода покоординатного спуска состоит в последовательной минимизации функции f(x1, x2, … ,xn) сначала в направлении координатной оси x1, затем в направлении координатной оси x2 и т. д. После окончания минимизации в направлении координатной оси xn цикл повторяется. Метод покоординатного спуска не требует вычисления производных функции f(x1, x2, … ,xn), поэтому целесообразно использовать критерии окончания вычислений в виде (2.21) или (2.22).
Опишем сначала алгоритм метода покоординатного спуска в общем виде.
Алгоритм 2.4 (Алгоритм метода покоординатного спуска).
Шаг 1. Выбрать произвольную начальную точку x(0) = (x 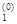 , x
, x 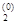 , … , x
, … , x 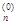 )T, например, x(0) = (0, 0, … , 0)T и погрешность вычислений e > 0. Вычислить f (x(0) ).
)T, например, x(0) = (0, 0, … , 0)T и погрешность вычислений e > 0. Вычислить f (x(0) ).
Шаг 2. Положить j =1.
Шаг 3. Рассмотреть функцию f(x1, x2, … ,xn) как функцию одной переменной xj, а все остальные переменные зафиксировать. Найти x 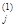 , решив задачу одномерной минимизации, т.е. найти
, решив задачу одномерной минимизации, т.е. найти 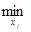 f(x1, x2, … ,xn).
f(x1, x2, … ,xn). 
Шаг 4. Если j < n, то положить j = j + 1 и перейти к шагу 3. В противном случае перейти к шагу 5.
Шаг 5. Найдено очередное приближение x(1) = (x 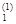 , x
, x 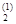 , …, x
, …, x 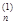 ). Проверить критерий окончания вычислений || x(1) – x(0)|| < e или |f(x(1)) – f(x(0))| < e. Если критерий окончания вычислений выполнен, то положить x* = x, f* = f(x*) и закончить вычисления. В противном случае положить x(0) = x(1) , f*(x(0)) = f(x(1)) и перейти к шагу 2.
). Проверить критерий окончания вычислений || x(1) – x(0)|| < e или |f(x(1)) – f(x(0))| < e. Если критерий окончания вычислений выполнен, то положить x* = x, f* = f(x*) и закончить вычисления. В противном случае положить x(0) = x(1) , f*(x(0)) = f(x(1)) и перейти к шагу 2.
На рис. 2.4 изображена геометрическая иллюстрация циклического покоординатного спуска.

Рис. 2.4
Применим метод покоординатного спуска для квадратичной функции f(x) = 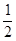 (Ax , x) + (b, x) + c с симметричной положительно определенной матрицей A .
(Ax , x) + (b, x) + c с симметричной положительно определенной матрицей A .
Выберем произвольную начальную точку x(0) = (x 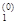 , x
, x 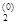 , … , x
, … , x 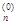 )T. Рассмотрим функцию f(x1, x
)T. Рассмотрим функцию f(x1, x 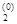 , … , x
, … , x 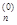 ) как функцию одной переменной x1, а все остальные переменные зафиксируем. Найдем значение x1 = x
) как функцию одной переменной x1, а все остальные переменные зафиксируем. Найдем значение x1 = x 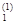 , при котором достигается
, при котором достигается 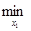 f(x1, x
f(x1, x 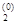 , … , x
, … , x 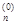 ).
).
При этом необходимо, чтобы
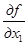 = 0.
= 0.
Это условие можно записать в следующем виде:
a11x1 + 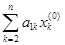 + b1 = 0,
+ b1 = 0,
x 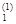 = –
= – 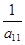 (
( 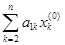 + b1).
+ b1).
Затем рассмотрим функцию f(x 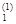 , x2, x
, x2, x 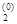 … , x
… , x 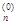 ) как функцию одной переменной x2, а все остальные переменные зафиксируем. Найдем значение x
) как функцию одной переменной x2, а все остальные переменные зафиксируем. Найдем значение x 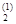 , при котором достигается
, при котором достигается 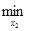 f(x
f(x 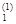 , x2, x
, x2, x 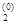 … , x
… , x 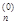 ). Пусть на очередном j-ом шаге функция f(x1, x2, … ,xn) рассматривается как функция одной переменной xj, а все остальные переменные зафиксированы. Значение xj, определяется из условия
). Пусть на очередном j-ом шаге функция f(x1, x2, … ,xn) рассматривается как функция одной переменной xj, а все остальные переменные зафиксированы. Значение xj, определяется из условия 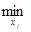 f(x
f(x 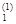 , x
, x 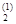 , … , x
, … , x 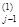 , xj, x
, xj, x 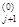 , …, x
, …, x 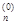 ). При этом необходимо, чтобы
). При этом необходимо, чтобы
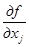 = 0.
= 0.
Это условие можно записать в следующем виде:
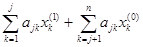 + bj = 0.
+ bj = 0.
Отсюда
x 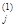 = –
= – 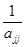 (
( 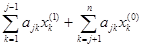 + bj). (2.27)
+ bj). (2.27)
В результате n шагов будет получено первое приближение x(1) = (x 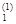 , x
, x 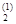 , …, x
, …, x 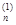 ). Затем итерационный процесс может быть продолжен. Опишем алгоритм этого процесса.
). Затем итерационный процесс может быть продолжен. Опишем алгоритм этого процесса.
Алгоритм 2.5 (Алгоритм метода покоординатного спуска для квадратичной функции).
Шаг 1. Для квадратичной функции f(x) = 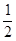
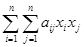 +
+ 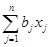 +с ввести матрицу A =(aij), вектор b = (b1, b2, … , bn)T и коэффициент c , i = 1, … , n; j = 1, … , n. Выбрать произвольную начальную точку x = (x1, x2, … , xn)T, например, x(0) = (x
+с ввести матрицу A =(aij), вектор b = (b1, b2, … , bn)T и коэффициент c , i = 1, … , n; j = 1, … , n. Выбрать произвольную начальную точку x = (x1, x2, … , xn)T, например, x(0) = (x 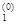 , x
, x 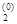 , … , x
, … , x 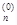 )T и погрешность вычислений e > 0. Вычислить f(x(0)).
)T и погрешность вычислений e > 0. Вычислить f(x(0)).
Шаг 2. В цикле по m = 0, …
В цикле по j =1, … , n вычислить
x 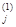 = –
= – 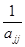 (
( 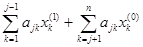 + bj).
+ bj).
Если верхний предел суммирования окажется меньше нижнего, то положить S = 0. Положить x(1) = x = (x 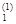 , x
, x 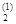 , … , x
, … , x 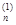 )T.
)T.
Шаг 3. Проверить выполнение критерия окончания вычислений:
||x(1) – x(0)|| = 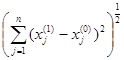 < e ,
< e ,
или
|f(x(1)) – f(x(0))| < e.
Если критерий окончания вычислений выполнен, то положить x* = x(1), f*min = f(x*) и закончить вычисления. В противном случае положить x(0) = x(1), f(x(0)) = f(x(1)) и перейти к шагу 2.
Пример 2.6.
Как и в предыдущих примерах, найдем минимум функции f(x) = x 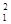 + 2x
+ 2x 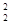 – 4x1 – 4x2 с точностью e = 0.1.
– 4x1 – 4x2 с точностью e = 0.1.
2 0
A = 0 4 ,
b = (– 4, – 4)T.
Как было показано ранее, эта функция имеет минимум в точке x* = (2, 1)T.
Применим метод покоординатного спуска.
Шаг 1. Возьмем начальное приближение x(0) =(x 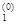 , x
, x 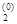 )T = (0, 0)T, положим e = 0.01. Вычислим f (x(0)) = 0.
)T = (0, 0)T, положим e = 0.01. Вычислим f (x(0)) = 0.
Шаг 2. Полагаем m = 0.
При j = 1 вычисляем x 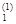 по формуле (2.27):
по формуле (2.27):
x 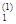 = –
= – 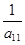 (
( 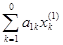 +
+ 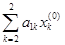 + b1).
+ b1).
Первая сумма равна нулю (верхний предел суммирования меньше нижнего), поэтому
x 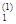 = –
= – 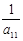 (a12x
(a12x 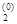 + b1) = –
+ b1) = – 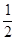 (0×0 – 4) = 2;
(0×0 – 4) = 2;
При j = 2 вычисляем x 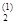 по формуле (2.27):
по формуле (2.27):
x 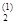 = –
= – 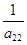 (
( 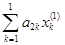 +
+ 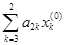 + b2).
+ b2).
Вторая сумма равна нулю (верхний предел суммирования меньше нижнего), поэтому
x 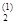 = –
= – 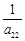 (a21x
(a21x 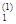 + b2) = –
+ b2) = – 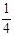 (0×2 – 4) = 1;
(0×2 – 4) = 1;
Итак, x(1) = (2, 1)T, т.е. найденное приближение совпадает с точным решением. Очевидно, f(x(1)) = –6.000.
Сходимость метода покоординатного спуска тем лучше, чем ближе направления осей эллипсов (линий уровня) к направлениям координатных осей, т. е. чем матрица A ближе к диагональной.
Метод Ньютона
Метод Ньютона использует информацию о производных первого и второго порядка. Поэтому он относится к градиентным методам второго порядка.
Метод Ньютона для функции многих переменных является обобщением метода Ньютона для одномерного случая (разд. 1.8)
Пусть дана дважды непрерывно дифференцируемая функция n переменных f(x) = f(x1, x2, … ,xn) и начальная точка x(0) = (x 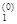 , x
, x 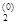 , … , x
, … , x 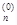 )T.
)T.
Разложим функцию f(x) в ряд Тейлора в точке x(0) как функцию многих переменных и ограничимся тремя членами:
f(x)=f(x(0)) + 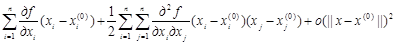 (2.28)
(2.28)
Пусть x(m) приближенное значение точки минимума, полученное на m-ом шаге итерационного процесса. Разложение (2.28) будет иметь место и для точки x(m), а именно
f(x)=f(x(m))+ 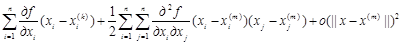 (2.29)
(2.29)
или в векторной форме
f(x) » f(x(m)) + (g(x(m)), (x – x(m)) + 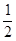 (G(x(m))(x – x(m)), (x – x(m))), (2.30)
(G(x(m))(x – x(m)), (x – x(m))), (2.30)
где G(x(m)) – матрица Гессе (матрица вторых производных) функции f(x) в точке x(m).
Из соотношения (2.29) видно, что в окрестности точки x(m) поведение функции f(x) может быть приближенно описано квадратичной функцией с точностью до величины порядка o(||x – x(m)||)2
Необходимое условие минимума – равенство нулю в точке минимума первой производной функции f(x), т. е.
f '(x) » g(x(m)) + G(x(m))(x – x(m)) = 0. (2.31)
Умножим (2.31) на G–1(x(m)):
G–1(x(m))g(x(m)) + (x – x(m)) = 0.
Следовательно,
x = x(m) – G–1(x(m))g(x(m)).
Пусть точка минимума x*» x(m+1). Тогда
x(m+1) = x(m) – G–1(x(m))g(x(m)). (2.32)
Формула (2.32) является расчетной формулой метода Ньютона.
Для квадратичной функции матрица Гессе есть матрица квадратичной формы, равенство (2.31) является точным, и решение (точка минимума) находится за одну итерацию. В общем случае метод Ньютона обеспечивает , как правило, быструю сходимость. Недостатком метода Ньютона является необходимость на каждой итерации вычисления матрицы Гессе и обратной к ней матрицы. Кроме того, если начальная точка выбрана недостаточно близко к точке минимума x*, то последовательность x(0), x(1), …, x(m), … может расходиться. Для избежания подобной ситуации используется обобщенный метод Ньютона, со следующей расчетной формулой:
x(m+1) = x(m) – a(m)G–1(x(m))g(x(m)). (2.33)
Формула (2.33) есть расчетная формула метода спуска (см. формулу (2.18)) с направлением в точке x(m), определяемым вектором p(m)= G–1(x(m))g(x(m)), и с шагом a(m).
Величина шага a(m) может быть выбрана из условия одномерной минимизации функции j(m)(a) = f(x(m) – a(m)G–1(x(m))g(x(m)).
Формулу (2.32) также можно рассматривать как формулу спуска с шагом a(m)= 1.
Опишем теперь алгоритм метода Ньютона.
Алгоритм 2.6 (Алгоритм метода Ньютона).
Шаг 1. Выбрать произвольную начальную точку x(0) = (x 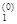 , x
, x 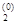 , … , x
, … , x 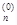 )T, например, x(0) = (0, 0, … , 0)T и погрешность вычислений e > 0.
)T, например, x(0) = (0, 0, … , 0)T и погрешность вычислений e > 0.
В цикле по m =0, …, пока не будет выполнен критерий окончания вычислений,
Шаг 2. Вычислить g(x(m)) и G(x(m)).
Шаг 3. Вычислить G–1(x(m)).
Шаг 4. Вычислить x(m+1) = x(m) – G–1(x(m))g(x(m)).
Вычисления продолжить до тех пор, пока не будет выполнен критерий окончания вычислений:
||x(m+1) – x(m)|| = 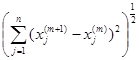 < e ,
< e ,
или
|f(x(m+1)) – f(x(m))| < e.
Если критерий окончания вычислений выполнен, то положить x* = x(m+1), f* = f(x*) и закончить вычисления.
В случае, когда f(x) – квадратичная функция, матрица Гессе есть матрица квадратичной формы и не зависит от x (G(x(m)) = A). Для этого случая получим следующий алгоритм.
Алгоритм 2.7 (Алгоритм метода Ньютона для квадратичной функции).
Шаг 1. Для квадратичной функции f(x) = 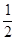
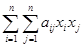 +
+ 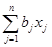 +с ввести матрицу A =(aij), вектор b = (b1, b2, … , bn)T и коэффициент c , i = 1, … , n; j = 1, … , n. Выбрать произвольную начальную точку x = (x1, x2, … , xn)T, например, x = (0, 0, … , 0)T и погрешность вычислений e > 0.
+с ввести матрицу A =(aij), вектор b = (b1, b2, … , bn)T и коэффициент c , i = 1, … , n; j = 1, … , n. Выбрать произвольную начальную точку x = (x1, x2, … , xn)T, например, x = (0, 0, … , 0)T и погрешность вычислений e > 0.
Шаг 2. Вычислить
g(x(0)) = (g 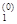 , g
, g 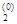 , … , g
, … , g 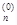 )T,
)T,
g 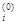 =
= 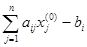 , i = 1, …, n.
, i = 1, …, n.
Шаг 3. Вычислить A–1.
Шаг 4. Вычислить x(1) = x(0) – A–1 g(x(0)) .
Пример 2.7.
Методом Ньютона найдем минимум функции f(x) = 2x 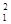 + 3x
+ 3x 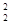 +x1x2 –3 x1 с точностью e = 0.1.
+x1x2 –3 x1 с точностью e = 0.1.
Шаг 1. Введем
4 1
A = 1 6 ,
b = (– 3, 0)T,
x(0)) = (0, 0)T.
Шаг 2. Вычислим
g(x(0)) = (g 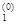 , g
, g 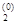 )T,
)T,
g 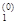 =
= 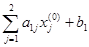 = 4×0 + 1×0 +(– 3) = – 3,
= 4×0 + 1×0 +(– 3) = – 3,
g 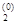 =
= 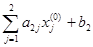 = 1×0 + 6×0 + 0 = 0.
= 1×0 + 6×0 + 0 = 0.
Шаг 3. Вычислим A–1 = (a ij). Элементы обратной матрицы находят по формуле (2.7) (разд. 2.1)
a ij = 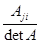 ,
,
где Aji – алгебраическое дополнениеэлемента aji матрицы A.
Для нашего примера
detA = 4×6 – 1×1 = 23,
A11 = a22 = 6, A12 = – a12 = –1, A21 = – a21 = – 1, A22 = a11 = 4.
Следовательно,
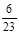
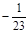
A–1 = .
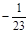

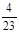
Шаг 4. Вычислим x(1) = x(0) – A–1 g(x(0)) .
Покоординатно
x(1) = (x 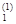 , x
, x 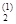 )T,
)T,
x 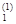 = x
= x 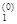 –
– 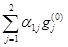 = 0 –
= 0 – 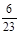 ×(–3) – (
×(–3) – ( 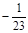 )×0 =
)×0 = 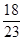 ,
,
x 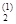 = x
= x 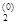 –
– 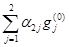 = 0 –(
= 0 –( 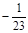 )×(–3) –
)×(–3) – 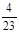 ×0 = –
×0 = – 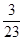 .
.
Точка x(1) = (x 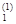 , x
, x 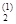 )T = (
)T = ( 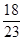 ,–
,– 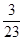 )T есть точка минимума.
)T есть точка минимума.
Дата добавления: 2018-09-23; просмотров: 2397; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
