Метод деления отрезка пополам (метод дихотомии)
СОДЕРЖАНИЕ
Введение
Тема 1. Задачи одномерной безусловной минимизации
1.1. Постановка задачи
1.2. Метод перебора
1.3. Метод поразрядного поиска
1.4. Метод деления отрезка пополам (метод дихотомии)
1.5. Метод Фибоначчи
1.6. Метод золотого сечения
1.7. Метод средней точки
1.8. Метод Ньютона
Тема 2. Задачи многомерной безусловной минимизации
2.1. Необходимые сведения из курса линейной алгебры
2.2. Постановка задачи многомерной оптимизации
2.3. Необходимые сведения из курса математического анализа
2.4. Методы спуска
2.5. Метод градиентного спуска с дроблением шага
2.6. Метод наискорейшего спуска
2.7. Метод сопряженных градиентов
2.8. Метод покоординатного спуска
2.9. Метод Ньютона
Тема 3. Задачи многомерной оптимизации при наличии ограничений. Линейное программирование
3.1. Постановка и классификация задач математического программирования
3.2. Постановка задачи линейного программирования
3.3. Графическое решение ЗЛП
3.4. Симплекс-метод
3.5. Метод искусственного базиса
Указания к выполнению лабораторных работ
Указания к выполнению типового расчета
Краткие сведения о математиках
Список литературы
ВВЕДЕНИЕ
Всякая задача, в которой ищется максимум или минимум некоторой функции n действительных переменных f(x1, x2, …, xn), относится к задачам оптимизации. Функция f(x1, x2, …, xn) называется целевой функцией. Если на переменные xi не наложено ограничений, т. е. -¥ < xi <¥, то задача оптимизации называется задачей безусловной оптимизации, в противном случае говорят о задаче условной оптимизации. В силу того, что max f(x1, x2, …, xn) = -min(-f(x1, x2, …, xn)), всегда можно свести задачу оптимизации к задаче минимизации. Учитывая это, будем в дальнейшем говорить о задаче минимизации функции f(x1, x2, …, xn).
|
|
|
Тема 1. Задачи одномерной безусловной минимизации
Постановка задачи
Пусть f(x) – действительная функция одной переменной, определенная на множестве X Ì (-¥, ¥). Точка x* Î X называется точкой локального минимума f(x) на множестве X, если существует такая e-окрестность этой точки, что для всех x из этой окрестности, т. е., если | x - x*| < e, выполняется условие f(x*) £ f(x). Если выполняется условие f(x*) < f(x), то x* называется точкой строгого локального минимума. У функции может быть несколько локальных минимумов. Точка x*Î X называется точкой глобального минимума f(x) на множестве X, если для всех x Î X выполняется условие f(x*) £ f(x). Значение функции f(x*) называется минимальным значением f(x) на множестве X, Для нахождения глобального минимума необходимо найти все локальные минимумы и выбрать наименьшее значение.
|
|
|
В дальнейшем будем рассматривать задачу нахождения локального минимума.
Известно, что для того, чтобы точка x* была точкой локального минимума дифференцируемой функции f(x), необходимо, чтобы выполнялось равенство
f '(x*) = 0. (1.1)
Точка x*, удовлетворяющая равенству (1.1), называется стационарной точкой. Если функция f(x) дважды дифференцируема, то для того, чтобы стационарная точка x* была точкой строгого локального минимума, достаточно, чтобы выполнялось неравенство
f ''(x*) > 0. (1.2)
Если дважды дифференцируемая функция f(x) задана на отрезке [a, b], то можно предложить следующий путь решения задачи нахождения глобального минимума:
1. Найти все стационарные точки на отрезке [a, b] из условия (1.1), т.е. найти корни уравнения f '(x) = 0, принадлежащие отрезку [a, b].
2. Найденные стационарные точки исследовать на выполнение условия (1.2), т.е. из найденных стационарных точек выделить точки локальных минимумов, для которых выполняется неравенство f ''(x) > 0.
3. Сравнить между собой значения f(x) на концах отрезка [a, b] и в точках локальных минимумов. Наименьшему из этих значений соответствует точка глобального минимума f(x) на отрезке [a, b].
|
|
|
Пусть функция f(x) определена на отрезке [a, b]. Функция f(x) называется унимодальной, если на этом отрезке имеется единственная точка x* локального минимума функции f(x), причем функция строго убывает при x £ x* и строго возрастает при x ³ x*. Многие алгоритмы минимизации функции одной переменной построены в предположении, что функция унимодальна на некотором отрезке. Этот отрезок будем называть отрезком локализации точки x*.
Из определения унимодальной функции вытекает следующее важное свойство. Пусть f(x) унимодальная функция на отрезке [a, b] и a £ x1 < x2 £ b. Тогда
если f(x1) £ f(x2), то x* Î [a, x2];
если f(x1) > f(x2), то x* Î [x1, b], (1.3)
где x* – точка минимума f(x) на отрезке [a, b].
Иллюстрация свойства (1.3) представлена на рис 1.1 и 1.2.
Рис. 1.1
Рис. 1.2.
Аналитический метод нахождения минимума функции одной переменной состоит в решении в явном виде уравнения (1.1) и проверке условия (1.2). Однако во многих случаях это или невозможно, или затруднительно. В таких случаях используются численные методы решения. Мы будем рассматривать методы прямого поиска, основанные на построении минимизирующих последовательностей x1, x2, …, xn, …,. Точки x1, x2, …, xn, … называют пробными точками.
|
|
|
Метод перебора
Этот метод является простейшим из прямых методов минимизации.
Пусть f(x) – унимодальная на отрезке [a, b] функция. Разобьем отрезок [a, b] на n равных частей точками x0, x1, x2, …, xn, так, что xi = a + ih , i = 0, 1, … , n , h = 
. Вычислим значения функции f(x) в точках xi и сравнив их, найдем точку xm, для которой f(xm) = 
f(xi).
За приближение x* примем xm.
Оценим погрешность метода перебора.
В силу выбора точки xm справедливы неравенства
f(xm –1) ³ f(xm), т.е. x* Î [xm –1, b];
f(xm) £ f(xm+1), т.е. x* Î [a , xm+1].
Следовательно, x* Î [xm –1, b]Ç [a , xm+1] = [xm –1, xm+1]. Длина отрезка [xm –1, xm+1] равна 
, и точка xm является его серединой. Поэтому
çxm – x*ç£ 
= e n.
Итак, чтобы обеспечить требуемую точность e определения минимума функции f(x) методом перебора, нужно число отрезков разбиения n выбрать из условия £ e, т.е.
n ³ 
. (1.4)
Пример 1.1.
Найдем минимум функции f(x) = x4 + e –x, x Î [0, 1] с точностью до e = 0.1.
Число отрезков разбиения найдем из условия (1.4):
n ³ 
= 10.
Определим величину шага h:
h = = 
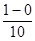= 0.1.
Вычислим значения функции f(x) в точках xi = a + ih = 0.1× i , i = 0, 1, … ,10. Эти значения представлены в таблице 1.1.
Таблица 1.1
| xi | 0.0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1.0 |
| f(xi) | 1.00 | 0.90 | 0.82 | 0.75 | 0.70 | 0.67 | 0.68 | 0.74 | 0.86 | 1.06 | 1.37 |
Из таблицы 1.1 видно, что минимальное из вычисленных значений есть f(0.5) = 0.67. Таким образом, x* » 0.5 и f(x*) » 0.67.
Метод поразрядного поиска
Этот метод представляет собой усовершенствование метода перебора. Поиск точки минимума функции осуществляется с переменным шагом. Вначале шаг полагается достаточно большим и грубо находится отрезок, содержащий точку минимума. Затем с более высокой точностью на этом отрезке находится искомая точка минимума.
Изложенная идея реализуется в методе поразрядного поиска следующим образом. Перебор точек отрезка происходит сначала с шагом D = xi+1– xi >e до тех пор, пока функция не начнет увеличиваться, т. е. не выполнится условие f(xi+1) ³ f(xi) или пока очередная точка не совпадет с правым концом отрезка [a, b], на котором ищется минимум функции f(x). После этого шаг уменьшается (обычно в четыре раза) и перебор точек производится в обратном направлении, справа налево, пока значения функции f(x) снова не станут увеличиваться или очередная точка не совпадет с левым концом отрезка и т. д. Процесс завершается, когда перебор в данном направлении закончен, и величина шага не превосходит заданной точности e.
Алгоритм 1.1 (Алгоритм метода поразрядного поиска).
Шаг 1. Ввести исходные данные: a, b, e.
Шаг 2. Выбрать начальный шаг D = 
. Положить x0 = a. Вычислить f(x0).
Шаг 3. Положить x1 = x0 + D. Вычислить f(x1).
Шаг 4. Сравнить f(x0) и f(x1). Если f(x0) > f(x1), то перейти к шагу 5, иначе – к шагу 6.
Шаг 5. Положить x0 = x1 и f(x0) = f(x1). Проверить условие x0 Î (a, b), т. е. a < x0< b. Если условие выполнено, перейти к шагу 3, иначе – к шагу 6.
Шаг 6. Проверка на окончание поиска. Если êD ê£ e, то вычисления завершить, положив x* » x0, f(x* ) » f(x0), иначе – перейти к шагу 7.
Шаг 7. Изменение направления и шага поиска. Положить x0 = x1 и f(x0) = f(x1), D = – 
. Перейти к шагу 3.
Пример 1.2.
Методом поразрядного поиска решим задачу, рассмотренную в примере 1.1: f(x) = x4 + e –x ® min, x Î [0, 1], e = 0.1.
Положим, что начальный шаг D = 
= 0.25.
Вычисляем последовательно f(xi) в точках xi с шагом D в направлении слева направо (от 0 к 1). Результаты вычислений представлены в таблице 1.2.
Таблица 1.2
| xi | 0.00 | 0.25 | 0.50 | 0.75 |
| f(xi) | 1.000 | 0.783 | 0.669 | 0.789 |
Вычисления в данном направлении прекращаются, потому что f(0.50) < f(0.75), причем êD ê> e. Продолжаем поиск в противоположном направлении, справа налево (от 0.75 к 0). Величину шага уменьшаем в 4 раза, положив D = –0.0625. Результаты вычислений представлены в таблице 1.3.
Таблица 1.3
| xi | 0.7500 | 0.6875 | 0.6250 | 0.5625 | 0.5000 | 0.4375 |
| f(xi) | 0.789 | 0.726 | 0.688 | 0.670 | 0.669 | 0.682 |
Так как f(0.5000) < f(0.4375) и êD ê= 0.0625 < e, вычисления прекращаются. Таким образом, x* » 0.5 и f(x*) » 0.669.
Метод деления отрезка пополам (метод дихотомии)
В основе этого метода лежит свойство унимодальной функции (1.3), благодаря которому можно сокращать отрезок локализации точки минимума.
Пусть f(x) – непрерывная и унимодальная на отрезке [a, b] функция, принимающая во всех точках этого отрезка конечные значения. Пусть число пробных точек x1, x2, …, xn конечно, и для определения каждой точки xk можно использовать информацию о значениях функции во всех предыдущих точках x1, x2, …, xk – 1 . Положим a0 = a, b0 = b. Середина отрезка [a, b] = [a0, b0] находится в точке 
. Выберем две симметричные точки
x1 = 
, x2 = 
. (1.5)
Величина d, удовлетворяющая условию 0 < d < b – a , является параметром метода, как правило, d – малая величина.
Вычислим значения функции в выбранных точках: f(x1) и f(x2). Определим новый отрезок локализации [a1, b1] следующим образом:
если f(x1) £ f(x2), то a1 = a0, b1 = x2;
если f(x1) > f(x2), то a1 = x1, b1 = b0.
Далее процедура деления отрезка [a1, b1] повторяется.
Деление продолжают до тех пор, пока половина длины отрезка [an, bn] не станет меньше заданной точности решения задачи e , e > d, т. е. пока не выполнится неравенство
< e .
Тогда за приближение x* принимают середину отрезка [an, bn], т.е. x* » 
.
Алгоритм 1.2 (Алгоритм метода дихотомии).
Шаг 1. Ввести исходные данные: a, b, d, e.
Шаг 2. Определить x1 и x2 по формулам (1.5).
Шаг 3. Вычислить f(x1) и f(x2).
Шаг 4. Если f(x1) £ f(x2), то перейти к новому отрезку [a, b], положив b = x2. Иначе перейти к новому отрезку [a, b], положив a = x1.
Шаг 5. Если 
< e, то требуемая точность достигнута, перейти к шагу 6, иначе – к шагу 2 для продолжения итераций.
Шаг 6. Положить x* » 
. Вычислить f *» f(x*).
Число итераций метода дихотомии оценивается по формуле
n ³ log2 
.
Величину d выбирают из условия 0 < d < 2e. При этом нужно иметь в виду, что при слишком малом d из-за погрешности вычисления на ЭВМ сравнение f(x1) и f(x2) становится затруднительным.
Пример 1.3.
Методом деления отрезка пополам решим задачу, рассмотренную в примерах 1.1 и 1.2: f(x) = x4 + e –x ® min, x Î [0, 1], e = 0.1.
Положим d = 0.02. Результаты вычислений приведены в табл. 1.4.
Таблица 1.4
| Номер итерации | a | b |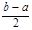 
| x1 | x2 | f(x1) | f(x2) | Сравнение f(x1) и f(x2) |
| 1 2 3 4 | 0 0.49 0.49 0.49 | 1 1.000 0.755 0.633 | 0.5 0.26 0.13 0.07 | 0.49 0.735 0.613 | 0.51 0.755 0.633 | 0.670 0.771 0.683 | 0.688 0.792 0.691 | f(x1) > f(x2) f(x1) < f(x2) f(x1) < f(x2) |
Вычисления прекращаются после 4-ой итерации, так как требуемая точность достигнута (0.07< 0.1). При этом
x* » 
» 0.56, f *» f(0.56*) » 0.67.
Метод Фибоначчи
Метод Фибоначчи эффективнее метода дихотомии, так как разбиение отрезка производится таким образом, что на каждой итерации требуется вычислять не два значения f(x1) и f(x2), а лишь одно.
Метод Фибоначчи основан на использовании чисел Фибоначчи, задаваемых рекуррентным соотношением
Fn = Fn -1 + Fn -2 (n ³ 2) (1.6)
с начальными значениями F0 = 1, F1 = 1.
Этот метод был предложен в 1953 г. Кифером.
Формула (1.6) вместе с начальными значениями определяет следующий ряд чисел Фибоначчи :
| n | 0 1 2 3 4 5 6 7 8 9 10 11 … |
| Fn | 1 1 2 3 5 8 13 21 34 55 89 144 … |
Метод Фибоначчи состоит из n шагов.
Положим вначале a0 = a, b0 = b.
На k -омшаге, k =0, 1, … , n – 1,определим точки x 
и x 
из условия
x = ak + 
(bk – ak), x = ak + 
(bk – ak). (1.7)
Формулы (1.7) являются основными расчетными формулами метода Фибоначчи
После этого так же, как и в методе дихотомии, определяют новый, меньший отрезок локализации [ak+1, bk+1] по тому же правилу:
если f(x ) £ f(x ), то ak+1 = ak, bk+1 = x ;
если f(x ) > f(x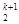 
), то ak+1 = x , bk+1 = bk.
Важно, что одна из пробных точек x , x станет пробной точкой на новом отрезке локализации, т. е. совпадет с одной из точек x 
, x 
.
Поэтому на каждой итерации достаточно определить только одно значение f(x), так как другое уже найдено на предыдущей итерации.
В конце вычислений можно взять в качестве приближенного значения x* = x 
.
После выполнения n итераций погрешность удовлетворяет следующему неравенству:
e n = 
< 
. (1.8)
Следовательно, если задана требуемая точность e, число итераций n определяется из условия 
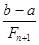< e или
Fn +1 >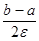 
. (1.9)
Заметим, что из (1.9) следует, что число итераций, необходимое для удовлетворения заданной точности e , зависит только от длины отрезка b – a и точности e и не зависит от вида функции f(x).
Алгоритм 1.3 (Алгоритм метода Фибоначчи).
Шаг 1. Ввести исходные данные: a, b, e. Определить число итераций n из условия (1.9). Ввести числа Фибоначчи F0, F1, F2, … , Fn +1.
Шаг 2. Положить k = 0 и определить x1и x2 по формулам (1.7).
Шаг 3. Вычислить f(x1) и f(x2).
Шаг 4. Проверить критерий окончания вычислений: k = n . Если k < n , перейти к шагу 5, иначе – к шагу 6.
Шаг 5. Перейти к новому отрезку локализации и новым пробным точкам.Если f(x1) £ f(x2), то положить b = x2, x2 = x1, f(x2) = f(x1), x1= a + (b – a) и вычислить f(x1). Иначе положить a = x1, x1 = x2, f(x1) = f(x2), x2 = a + 
(b – a) и вычислить f(x2).
Положить k = k +1и перейти к шагу 4.
Шаг 6. Положить x* » x1. Вычислить f *» f(x*).
Пример 1.4.
Методом Фибоначчи решим задачу, рассмотренную ранее: f(x) = x4 + e –x ® min, x Î [0, 1], e = 0.1.
Условие (1.8) для нашей задачи имеет вид
Fn +1 > 
= 5.
Первым среди чисел Фибоначчи, для которого выполняется это условие является число F5 = 8, т.е. n +1 = 5, n = 4.
Результаты вычислений для четырех итераций приведены в табл. 1.5.
Таблица 1.5
| k | a | b | b – a | x1 | x2 | f(x1) | f(x2) | Сравнение f(x1) и f(x2) |
| 0 1 2 3 | 0 0.375 0.375 0.375 | 1 1.000 0.75 0.625 | 1 0.625 0.375 0.25 | 0.375 0.625 0.5 0.5 | 0.625 0.75 0.625 0.5 | 0.707 0.688 0.669 0.669 | 0.688 0.789 0.688 0.669 | f(x1) > f(x2) f(x1) < f(x2) f(x1) < f(x2) |
Таким образом, x* » 0.5 и f(x*) » 0.669.
Метод золотого сечения
В основе этого метода лежит понятие "золотого сечения", введенного Леонардо да Винчи и используемого, в частности, при построении архитектурных сооружений античности и эпохи Возрождения.
Золотым сечением отрезка называется его разбиение на две неравные части, так, что отношение длины всего отрезка к длине его большей части равно отношению длины большей части к длине меньшей части (рис.1.3, слева)
= 
.
Рис 1.3
Золотое сечение осуществляется двумя точками x1 и x2, расположенными симметрично относительно середины отрезка (рис.1.3, справа). Нетрудно проверить, что
= = 
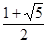, (1.10)
= 
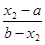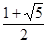= . (1.11)
Точка x1 осуществляет золотое сечение не только отрезка [a, b], но и отрезка [a, x2], а точка x2 осуществляет золотое сечение не только отрезка [a, b], но и отрезка [x1, b]. Действительно,
= 
= ,
= 
= .
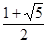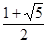Из (1.10) и (1.11) получаем:
x1 = a + 
, x2 = a + 
. (1.12)
Формулы (1.12) являются основными расчетными формулами метода золотого сечения.
Из (1.12) следует, что x1 + x2 = a + b. Если обозначить r =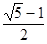 
, то формулы (1.12) можно переписать так:
x1 = b – r(b – a), x2 = a + r(b – a) (1.13)
Процедура деления отрезка [a, b] такая же, как и для методов дихотомии и Фибоначчи. Вычисляются значения функции в выбранных точках: f(x1) и f(x2). Определяется новый отрезок локализации [a1, b1] следующим образом:
если f(x1) £ f(x2), то a1 = a, b1 = x2;
если f(x1) > f(x2), то a1 = x1, b1 = b.
Далее процедура деления отрезка [a1, b1] повторяется с использованием формул (1.12) или (1.13).
Так же, как и в методе Фибоначчи, одна из пробных точек x1, x2станет пробной точкой на новом отрезке локализации. Поэтому на каждой итерации достаточно определить только одно значение f(x), так как другое уже найдено на предыдущей итерации.
В конце вычислений можно взять в качестве приближенного значения x* середину последнего из полученных отрезков.
После выполнения n итераций погрешность удовлетворяет следующему неравенству:
e n = 
< 
.
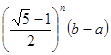Условием окончания вычислений является выполнение неравенства e n < e .
Алгоритм 1.4 (Алгоритм метода золотого сечения).
Шаг 1. Ввести исходные данные: a, b, e. Положить r = 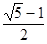, e n = 
.
Шаг 2. Определить x1и x2 по формулам (1.13).
Шаг 3. Вычислить f(x1) и f(x2).
Шаг 4. Проверить критерий окончания вычислений. Если e n < e , перейти к шагу 5, иначе – к шагу 6.
Шаг 5. Перейти к новому отрезку локализации и новым пробным точкам.Если f(x1) £ f(x2), то положить b = x2, x2 = x1, f(x2) = f(x1), x1 = b – r(b – a) и вычислить f(x1). Иначе положить a = x1, x1 = x2, f(x1) = f(x2), x2 = a + r(b – a) и вычислить f(x2).
Положить e n = r e n и перейти к шагу 4.
Шаг 6. Положить x* » 
. Вычислить f *» f(x*).
Пример 1.5.
Методом золотого сечения решим задачу, рассмотренную ранее: f(x) = x4 + e –x ® min, x Î [0, 1], e = 0.1.
Результаты вычислений приведены в табл. 1.6.
Таблица 1.6
| Номер итерации | a | b | e n | x1 | x2 | f(x1) | f(x2) | Сравнение f(x1) и f(x2) |
| 1 2 3 4 5 | 0 0.382 0.382 0.382 0.472 | 1 1.000 0.764 0.618 0.618 | 0.5 0.309 0.191 0.118 0.073 | 0.382 0.618 0.528 0.472 | 0.618 0.764 0.618 0.528 | 0.704 0.685 0.668 0.673 | 0.685 0.807 0.685 0.668 | f(x1) > f(x2) f(x1) < f(x2) f(x1) < f(x2) f(x1) > f(x2) |
Вычисления прекращаются после 5-ой итерации, так как требуемая точность достигнута (0.073 < 0.1).
Таким образом, x* » 
» 0.55 и f(x*) » 0.67.
Метод средней точки.
Все методы, рассмотренные до сих пор, основаны на предположении об унимодальности исследуемой функции. Эти методы используют вычисление значений функции в некоторых точках и не требуют вычисления значений производной функции. Использование информации о производной позволит повысить эффективность решения задачи оптимизации.
Рассмотрим метод средней точки, который называется также методом бисекции или методом деления отрезка пополам.
Пусть f(x) – унимодальная, непрерывно дифференцируемая на отрезке [a, b] функция и на этом отрезке точка x* является единственной стационарной точкой. Сведем задачу нахождения минимума функции f(x) к решению нелинейного уравнения
f '(x) = 0. (1.14)
Положим a0 = a, b0 = b.
Так как функция f '(x) удовлетворяет условию (1.14), то она принимает на концах отрезка [a0, b0] значения разных знаков, т.е.
f(a0)f(b0) < 0.
Разделим отрезок [a0, b0] пополам. Получим точку x0 = 
. Вычислим f '(x0). Если f '(x0) = 0, то x0 – искомый корень, и задача решена. Если f '(x0) ¹ 0, то f '(x0) – число определенного знака: f '(x0) > 0, либо f '(x0) < 0. Тогда либо на концах отрезка [a0, x0], либо на концах отрезка [x0, b0] значения функции f '(x) имеют разные знаки. Обозначим такой отрезок [a1, b1]. Очевидно, что x*Î [a1, b1], и длина отрезка [a1, b1] в два раза меньше, чем длина отрезка [a0, b0]. Поступим аналогично с отрезком [a1, b1]. В результате получим либо корень x*, либо новый отрезок [a2, b2], и т.д. (рис.1.4 ).
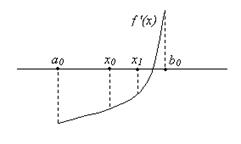
Рис. 1.4
Середина n-го отрезка xn = 
. Очевидно, что длина отрезка [an, bn] будет равна 
, а т. к. x*Î [an, bn], то
| xn – x*| £ 
£ 
. (1.15)
Оценка (1.15) характеризует погрешность метода средней точки и указывает на скорость сходимости: метод сходится со скоростью геометрической прогрессии, знаменатель которой q = 1/2.
Если задана требуемая точность e , то процесс вычислений следует закончить, когда выполнится условие ê f '(xn) ê£ e, после чего полагают x* » xn.
Алгоритм 1.5 (Алгоритм метода средней точки).
Шаг 1. Ввести исходные данные: a, b, e.
Шаг 2. Определить x0 = .
Шаг 3. Вычислить f '(x0).
Шаг 4. Проверить критерий окончания вычислений. Если êf '(x0) ê£ e, , перейти к шагу 6, иначе – к шагу 5.
Шаг 5. Перейти к новому отрезку локализации [a, b].Если f '(x0) > 0, то положить b = x0. Иначе положить a = x0. Перейти к шагу 2.
Шаг 6. Положить x* » x0. Вычислить f'(x*).
Пример 1.6.
Методом средней точки решим задачу, рассмотренную ранее:
f(x) = x4 + e - x ® min, x Î [0, 1], e = 0.02.
Очевидно, что f '(x) = 4x3 – e –x.
Результаты вычислений приведены в табл. 1.7.
Таблица 1.7
| Номер итерации | a | b | x0 | f '(x0) | Знак f '(x0) |
| 1 2 3 4 5 | 0 0.5 0.5 0.5 0.5 | 1 1.000 0.750 0.625 0.563 | 0.5 0.750 0.625 0.563 0.531 | -0.107 1.215 0.441 0.142 0.012 | – + + + |
Вычисления прекращаются после 5-ой итерации, так как требуемая точность достигнута (0.012 < 0.02).
Таким образом, x* » 0.531 и f(x*) » 0.668.
Метод Ньютона.
Пусть f(x) – дважды непрерывно дифференцируемая функция, причем f ''(x) > 0. Тогда, как уже указывалось в предыдущем разделе, решение задачи минимизации функции f (x) сводится к решению нелинейного уравнения f '(x) = 0.
Метод Ньютона является наиболее эффективным методом решения нелинейных уравнений.
Пусть корень x* Î [a, b], так, что f '(a)f '(b) < 0. Положим x0 = b . Проведем касательную к графику функции y = f '(x) в точке B0 = (x0, f '(x0)) (рис. 1.5).
Рис. 1.5
Уравнение касательной будет иметь вид:
y – f '(x0) = f "(x0)(x – x0). (1.16)
Первое пересечение получим, взяв абсциссу точки пересечения этой касательной с осью OX, т. е. положив в (1.16) y = 0, x = x1:
x1 = x0 – 
. (1.17)
Аналогично поступим с точкой B1(x1, f '(x1)), затем с точкой B2(x2, f '(x2)), и т. д. в результате получим последовательность приближений x1, x2, …, xn , …, причем
xn +1 = xn – 
. (1.18)
Формула (1.18) является расчетной формулой метода Ньютона.
При заданной точности e > 0 вычисления по формуле (1.18) нужно вести до тех пор, пока не будет выполнено неравенство| f '(xn)| £ e , после чего полагают x* » xn.
Алгоритм 1.6 (Алгоритм метода Ньютона).
Шаг 1. Ввести исходные данные: a, b, e. Положить n = 0, x0 = b.
Шаг 2. Вычислить f '(xn) и f "(xn).
Шаг 3. Вычислить xn +1 = xn – .
Шаг 4. Проверить критерий окончания вычислений. Если êf '(x n +1) ê£ e, , перейти к шагу 6, иначе – к шагу 5.
Шаг 5. Положить n = n +1.Перейти к шагу 2.
Шаг 6. Положить x* » xn +1 . Вычислить f'(x*).
Пример 1.7.
Методом Ньютона найдем точку минимума функции f(x) = xarctgx – 
ln(1 + x2 ) на отрезке [0, 1], e = 10 –7.
Функция f(x) дважды дифференцируема, причем
f '(x) = arctgx, f "(x) = 
> 0.
Расчетные формулы (1.18) примут вид:
xn +1 = xn – arctgx(1 + x2).
Результаты вычислений приведены в табл. 1.8.
Таблица 1.8
| n | xn | f '(xn) |
| 0 1 2 3 4 | 1 -0.570 0.117 -0.061×10-3 9×10-8 | 0.785 -0.519 0.116 -1.061×10-3 9×10-8 |
Вычисления прекращаются, так как требуемая точность достигнута (9×10-8 < 10 –7).
Таким образом, x* » 9×10-8 » 0, f(x*) » 0.
Дата добавления: 2018-09-23; просмотров: 4244; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!