Тема 2. Задачи многомерной безусловной минимизации

Необходимые сведения из курса линейной алгебры

Пусть f(x₁, x₂, … ,x_n) – действительная функция n переменных, определенная на множестве X Ì Rⁿ(Rⁿ – n-мерное пространство, в частности, R² – плоскость). Обозначим через x вектор-столбец

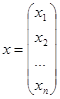= (x₁, x₂, …, x_n)^T, (2.1)

где символ "T" – знак транспонирования. Тогда x –точка в пространстве Rⁿ и f(x) =f(x₁, x₂, … ,x_n).

Скалярное произведение векторов x = (x₁, x₂, …, x_n)^T и y = (y₁, y₂, …, y_n)^T определяется следующим образом:

(x, y) = 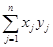. (2.2)

Нормой (длиной) вектора x называется число

||x|| = 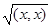= 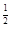. (2.3)

Определено расстояние между векторами x и y:

r(x, y) = ||x – y|| = . (2.4)

Матрица A =(a_ij), i = 1, … , m; j = 1, … , n, представляет собой прямоугольную таблицу размера m´n, состоящую из m строк и n столбцов. В частности, вектор-столбец x является матрицей размера n ´1.

Квадратная матрица A называется симметрической, если a_ij = a_ji , i , j = 1, … , n .

Произведением матрицы A размера m´n на вектор-столбец x Î Rⁿ является вектор-столбец b = (b₁, b₂, … , b_m)^TÎ R^m, координаты которого вычисляются по формуле:

b_i = 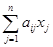= (aⁱ, x) , i = 1, 2, …, m, (2.5)

где aⁱ = (a_i₁, … , a_in) – i-ая строка матрицы A, т. е. Ax = b.

Определителем квадратной матрицы A (обозначается detA или |A|) размера n´n называется число, которое определяется по формуле:

detA = |A| = . (2.6)

Здесь A_ij – алгебраическое дополнение элемента a_ij, A_ij = (–1)ⁱ⁺^j M_ij , а M_ij – минор, который является определителем матрицы, полученной из A вычеркиванием i-ой строки и j-го столбца.

Если определитель матрицы A не равен нулю, то существует обратная матрица A^–1 = (a _ij). Элементы обратной матрицы находят по формуле:

a _ij = 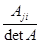, (2.7)

где A_ji – алгебраическое дополнениеэлемента a_ji матрицы A.

Квадратичной формой Q от n переменных x₁, x₂, …, x_n называется сумма, каждый член которой является либо квадратом одного из этих переменных, либо произведением двух разных переменных. Считая, что в квадратичной форме Q уже сделано приведение подобных членов, введем следующие обозначения: коэффициент при x 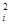обозначим через a_ii, а коэффициент при произведении x_ix_j для i ¹ j – через 2a_ij. Член 2a_ijx_ix_j можно записать в виде

2a_ijx_ix_j = a_ijx_ix_j + a_jix_jx_i.

Очевидно, что a_ij = a_ji. Всю квадратичную форму Q можно записать в виде суммы всевозможных членов a_ijx_ix_j, где i и j независимо друг от друга принимают значения от 1 до n:

Q = 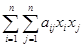. (2.8)

В частности, при i = j получается член a_iix .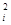

Из коэффициентов a_ij можно составить квадратную матрицу A = (a_ij)размера n´n; она называется матрицей квадратичной формы Q.

Так как a_ij = a_ji, матрица A является симметрической.

Квадратичную форму Q можно записать в ином виде, используя введенное ранее умножение матрицы на вектор-столбец и скалярное произведение векторов. Равенство (2.8) равносильно равенству

Q(x) = 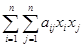= (Ax , x). (2.9)

Квадратичная форма Q(x) называется положительно определенной, если для всех x ¹ 0 имеет место неравенство Q(x) > 0.

Из курса линейной алгебры известен критерий Сильвестра положительной определенности квадратичной формы: для того, чтобы квадратичная форма Q(x) была положительно определенной, необходимо и достаточно, чтобы ее матрица A = (a_ij) была положительно определена, т. е. все ее угловые миноры были положительными:

a₁₁ . . . a₁₂

a₁₁ a₁₂. ._.

D₁ = a₁₁ > 0; D₂ = > 0; D _n = . . > 0. (2.10)

a₂₁a₂₂ . .

a₁₁ . . . a₁₂

Дата добавления: 2018-09-23; просмотров: 279; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 123 4 Следующая ⇒

Мы поможем в написании ваших работ!