Краткие теоретические сведения

 

В теории автоматического управления часто используют операторную форму записи дифференциальных уравнений. При этом вводится понятие дифференциального оператораp = d/dt так, что, dy/dt = py, а pⁿ = dⁿ/dtⁿ. Это лишь другое обозначение операции дифференцирования. Обратная дифференцированию операция интегрирования записывается как 1/p.

В теории автоматического управления широко применяется операторный метод описания линейных систем автоматического управления, использующий интегральное преобразование Лапласа (L – преобразование)

  Данное преобразование называется прямым односторонним преобразованием Лапласа, преобразует функцию времени х(t) – оригинал, в функцию комплексной переменной X (р) - изображение.

Передаточной функцией называется отношение величины выходного параметра, к величине входного параметра, преобразованных по Лапласу, при нулевых начальных условиях.

 

Пример решения

 

а) Дано дифференциальное уравнение, характеризующее динамику технологического объекта,

.

     Если обозначить Y(s), X(s) и U(s) как изображения сигналов y, x и u соответственно, то операторное уравнение (при нулевых начальных условиях) в данном случае примет вид:

6,25s²Y(s) + 4sY(s) + Y(s) = 9X(s) – 1,2sX(s) - 5sU(s).

     Данное уравнение можно преобразовать, вынеся Y(s) и X(s) за скобки:

Y(s)^. (6,25s² + 4s + 1) = X(s)^. (9 – 1,2s) - 5sU(s).

     Отсюда получено:

.

Если обозначить передаточные функции объекта как

,

то получается уравнение Y(s) = W_x(s)^.X(s) + W_u(s)^.U(s). Структурная схема объекта приведена на рисунке 1.

 

     Полученные передаточные функции имеют одинаковые знаменатели, называемые характеристическими выражениями:

A(s) = 6,25s² + 4s + 1.

2

     Если приравнять данное выражение к нулю, то образуется характеристическое уравнение 6,25s² + 4s + 1 = 0, корни которого

 и .

                                                                                               Распределение корней на комплексной плоскости показано на рис. 2. По рисунку видно, что корни лежат в левой полуплоскости, следовательно, объект устойчив.

 

б) Дана передаточная функция вида

.

     Для записи дифференциального уравнения необходимо учесть, что по определению , откуда получено:

,

Y(s) (s – 0,5)(3s² + 2) = X(s) (7s³ + 5,5),

Y(s) (3s³ + 2s – 1,5s² – 1) = X(s) (7s + 5,5),

3s³ Y(s) + 2s Y(s) – 1,5s² Y(s) – Y(s) = 7s X(s) + 5,5 X(s).

 

     Теперь, если применить обратное преобразование Лапласа, получается:

                               .

 

     2.4. Задания:

 

а) По заданным дифференциальным уравнениям определить операторные уравнения при нулевых начальных условиях, передаточные функции, структурные схемы звеньев, характеристические уравнения и их корни. Показать распределение корней на комплексной плоскости.

Оценить устойчивость каждого из звеньев.

б) По заданной передаточной функции записать дифференциальное уравнение.

 

Вариант № 1

     а) ; y(0) = 1; y’(0) = 2;

б) ; y(0) = 10; y’(0) = 6.

     .

Вариант № 2

     а) ;  y(0) = -2; y’(0) = 0;

     б) ;  y(0) = -1; y’(0) = 2; y’’(0) = 1.

     .

Вариант № 3

     а) ; y(0) = 3; y’(0) = 1;

б) 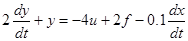; y(0) = 2; y’(0) = -18.

     .

Вариант № 4

     а) ; y(0) = -1; y’(0) = 2;

б) ;   y(0) = 15; y’(0) = -2.

     .

Вариант № 5

     а) ; y(0) = 3; y’(0) = -11;

б) ;      y(0) = 1; y’(0) = 2; y’’(0) = -1.

     .

Вариант № 6

     а) ;       y(0) = 1; y’(0) = 2; y’’(0) = -1;

б) ; y(0) = 0; y’(0) = -10; y’’(0) = 1.

     .

Вариант № 7

     а) ;    y(0) = 1; y’(0) = 7;

б) ; y(0) = -3; y’(0) = 5. .

Вариант № 8

     а) ;   y(0) = -1; y’(0) = 4;

б) 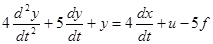; y(0) = 9; y’(0) = -4.

     .

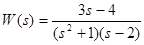Вариант № 9

     а) ; y(0) = -2; y’(0) = 3; y’’(0) = 1;

б) ;          y(0) = 0.5; y’(0) = 1.

     .

Вариант № 10

     а) ; y(0) = y’’(0) = 10;    y’(0) = 1;

б) 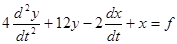;            y(0) = 9; y’(0) = -1.

     .

Вариант № 11

     а) ; y(0) = 0; y’(0) = -1; y’’(0) = 1;

б) ;  y(0) = 1; y’(0) = 0; y’’(0) = 12.

     .

Вариант № 12

     а) ; y(0) = 5; y’(0) = 3;

б) ;  y(0) = -2; y’(0) = 1.

     .

Вариант № 13

     а) 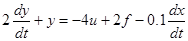; y(0) = 2; y’(0) = 8;

б) ; y(0) = -2; y’(0) = 2.

     .

Вариант № 14

     а) 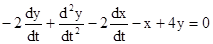; y(0) = 7; y’(0) = -2;

б) ; y(0) = 5; y’(0) = -1.

     .

Вариант № 15

     а) ;      y(0) = 1; y’(0) = 2; y’’(0) = -3;

б) 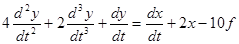; y(0) = 2; y’(0) = -1; y’’(0) = 1.

     .

Вариант № 16

     а) ;    y(0) = 1; y’(0) = 2;

б) ;   y(0) = -1; y’(0) = 4.

     .

Вариант № 17

     а) 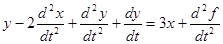;   y(0) = -1; y’(0) = 1;

б) ; y(0) = 3; y’(0) = -2.

     .

Вариант № 18

     а) ;            y(0) = 5; y’(0) = 1;

б) ;          y(0) = y’’(0) = 4; y’(0) = 2.     .

Вариант № 19

     а) ;            y(0) = 1; y’(0) = -2;

б) ;      y(0) = -2; y’(0) = 4.

     .

Вариант № 20

     а) 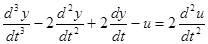; y(0) = 0; y’(0) = -2; y’’(0) = 1;

б) ;  y(0) = 1; y’(0) = 0; y’’(0) = 2.

     .

Вариант № 21

     а) ; y(0) = 5; y’(0) = 4;

б) ; y(0) = 3; y’(0) = 2.

     .

Вариант № 22

     а) ;      y(0) = 2; y’(0) = 2; y’’(0) = -1;

б) ; y(0) = 5; y’(0) = -2.

     .

Вариант № 23

     а) ; y(0) = 2; y’(0) = 4;

б) ;           y(0) = -1; y’(0) = 2.

     .

Вариант № 24

     а) 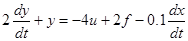; y(0) = 2; y’(0) = 4;

б) ; y(0) = -3; y’(0) = 1.

     .

 

        2.5. Контрольные вопросы

 

1. Операторные методы исследования САУ.

2. Преобразование Лапласа.

3. Основные свойства преобразования Лапласа.

4. Передаточная функция САУ.

5. Корневые критерии устойчивости САУ.

---

Дата добавления: 2018-09-23; просмотров: 837; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!