Как средство описания предпочтительности исходов
При изучении проблем построения целенаправленных систем и принятия оптимальных решений всегда приходится учитывать цели, желания и нужды тех, кто управляет такими системами или ставится перед необходимостью принятия решения. Именно поэтому исследование полезности представляет собой основу теории и практики исследования операций и теории игр.
Термин "полезность" имеет два разных значения.
Первое - это качественная, или сравнительная оценка, характеризуемая такими утверждениями, как: "Я ценю это больше, чем то" или "Я предпочитаю Х, а не Y". Второе значение этого термина - количественная оценка, когда мы в виде числа выражаем наше предпочтение, пытаясь отразить его сравнительную природу.
Учитывая такую двойственность, будем использовать термин "ПРЕДПОЧТЕНИЕ" для отображения качественной характеристики объекта, а термин "ПОЛЕЗНОСТЬ" - для количественного представления предпочтений.
Так, например, в шахматах предпочтение той или иной стратегии невозможно оценить количественно. Здесь возможна только качественная оценка: "Этот ход лучше, сильнее". В этом случае применимо отношение "предпочтения". При решении задач перевозки грузов, размещения заказов, распределения боевых средств по объектам поражения и т.п. применимо отношение "полезности" с количественной оценкой целевой функции, на основании которого отдают предпочтение тому или другому решению. Это описывается в виде некоторого абстрактного отношения - бинарного.
|
|
|
Для дальнейшего изложения материала рассмотрим некоторые основополагающие понятия теории множеств [8/20].
1. МНОЖЕСТВОМ принято называть совокупность различимых между собой объектов одинаковой природы. Каждый из таких объектов в отдельности есть ЭЛЕМЕНТ МНОЖЕСТВА. Принадлежность некоторого элемента е множеству Е обозначается еÎ Е. Множества Е1 и Е2 равны (Е1=Е2), если они содержат одни и те же элементы.
2. Множество Е' представляет собой некоторое ПОДМНОЖЕСТВО множества Е (обозначается Е'ÍЕ), если каждый элемент, принадлежащий Е', одновременно принадлежит и Е. Множество называется ПУСТЫМ МНОЖЕСТВОМ (Е'=0), если оно не содержит ни одного элемента.
3. ПЕРЕСЕЧЕНИЕ МНОЖЕСТВ Е1 И Е2 (обозначается Е1∩Е2) есть множество всех элементов е, содержащихся и в Е1, и в Е2 (рис. 1.1).
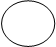
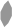

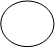

Е1 Е2 Е1 Е2
Е1 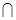 Е2
Е2 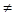 0 Е1
0 Е1 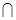 Е2 = 0
Е2 = 0
Рис. 1.1. Рис. 1.2.
Множества Е1 и Е2 являются непересекающимися, если отсутствуют элементы, входящие одновременно и в Е1, и в Е2 (рис. 1.2).
4. ОТНОШЕНИЕМ, существующим на множестве Е, называется форма связи между элементами или подмножествами этого множества. Отношения определяются словами ("быть меньше, чем ...", "обладать свойствами делимости на ...", "быть одинаковым с ...") или символами, если они общеприняты ("=", "<", ">", " 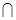 ").
").
|
|
|
5. Числовое множество Е называется УПОРЯДОЧЕННЫМ, если любые два его элемента е1 и е2 связаны либо отношением е1>е2, либо отношением е1<е2. Например, множество всех действительных чисел. Те или иные отношения могут существовать и между элементами различных множеств.
БИНАРНОЕ ОТНОШЕНИЕ является фундаментальным понятием в теории предпочтений. Математические справочники трактуют, что бинарное отношение это двуместный предикат на заданном подмножестве. А предикат - это функция, позволяющая определить логические законы, взаимные соотношения упорядоченных элементов непустого множества. Объединив эти два определения, можем сказать, что БИНАРНОЕ ОТНОШЕНИЕ - это функция, позволяющая определить логические законы и взаимные соотношения упорядоченных пар (x,y) элементов заданного множества Х.
 Бинарное отношение R на непустом множестве X есть подмножество множества всех упорядоченных пар элементов Х, которое задается прямым произведением Х х Х = {(x,y): xÎX, yÎX}. Запись xRy (читается: x находится в отношении R к y) означает, что (x,y) принадлежит R; аналогично не xRy (записывается как xRy) означает, что (х,y) не принадлежит R или, что x не находится в отношении R к y. То есть, тот факт, что игрок (или коалиция игроков) предпочитает ситуацию x ситуации y записывается в виде xfy (иногда в виде x fky).
Бинарное отношение R на непустом множестве X есть подмножество множества всех упорядоченных пар элементов Х, которое задается прямым произведением Х х Х = {(x,y): xÎX, yÎX}. Запись xRy (читается: x находится в отношении R к y) означает, что (x,y) принадлежит R; аналогично не xRy (записывается как xRy) означает, что (х,y) не принадлежит R или, что x не находится в отношении R к y. То есть, тот факт, что игрок (или коалиция игроков) предпочитает ситуацию x ситуации y записывается в виде xfy (иногда в виде x fky).
|
|
|
В теории предпочтений используются два основных бинарных соотношения на множестве Х. Во-первых, отношение нестрогого предпочтения f. Запись x f y читается: "х либо предпочтительнее, чем y, либо безразличен к y". Чаще пользуются формулировкой: "y не предпочтительнее, чем x"). Во-вторых, применяется отношение строгого предпочтения f. Запись x f y читается так: "x предпочтительнее, чем y".
На вопрос о том, какое из двух отношений (f или f ) взять в качестве основного бинарного отношения, каждый отвечает в соответствии со своими личными вкусами. Поскольку автор предпочитает отношение f, то оно будет во всех дальнейших рассуждениях выполнять роль основного бинарного отношения.
Способы описания игр
Существует ряд способов описания и анализа конкретных игр.
|
|
|
Один из приемов описания игр состоит в том, что игра представляется в виде ТОПОЛОГИЧЕСКОГО ДЕРЕВА (рис.1.3), на котором выделяются начальная вершина игры А, промежуточные вершины (позиции) и множество конечных вершин, отвечающих окончательным позициям игры, то есть указывается, какие ходы могут делать игроки, какой информацией во время игры они располагают, какие варианты можно выбирать и какими могут быть предельные размеры выигрышей в конце игры.
Игра, описанная таким образом, называется игрой в РАЗВЕРНУТОЙ (ЭКСТЕНСИВНОЙ) ФОРМЕ. На рис.1.3 показано дерево игры для упрощенной игры двух лиц в покер. В этой игре ставка каждого из игроков равна 5 долларам. После сдачи карт на руках у игроков остается определенное количество карт. Набор карт может быть либо старшим (С), либо младшим (М). У игрока 1 имеется две возможности: либо раскрыть карты (Р), либо повышать игру (В). При раскрытых картах старшая карта выигрывает банк; если карты игроков равны, то банк делится пополам.
Если игрок 1 повышает игру, то он вкладывает в банк еще 5 долларов. У игрока 2 после этого имеется 2 альтернативы: либо пасовать (П), либо уравнивать (У). Если он пасует, то игрок 1 выигрывает банк при любых картах. Если же игрок 2 уравнивает игру, то он вносит в банк еще 5 долл., после чего либо старшая карта выигрывает банк, либо при равных картах банк делится пополам. На дереве игры (рис. 1.3) изображены все возможные ситуации игры и указаны соответствующие им платежи.

 А
А
 I
I
(С,С) (С,М) (М,С) (М,М)







 .
.
II
III
Р В Р В Р В Р В
 | 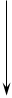 |  | |||||||||||||
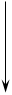 | 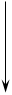 |  | 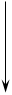 |  | |||||||||||
IV
П У П У П У П У
 |  |  |  |  |  |  | |||||||||
 | |||||||||||||||
V
0 5 0 5 5 10 -5 5 -10 0 5 0
Рис. 1.3. Дерево игры для игры в развернутой форме
(на примере упрощенной игры двух лиц в покер со ставкой 5 долл.).
I - ход 1: определение ставок и сдача карт (случайный ход);
II - ситуация после сдачи карт: С-старшая, М-младшая;
III - ход 2: игрок 1 либо раскрывает карты (Р), либо повышает игру (В);
IV - ход 3: Если игрок 1 повышает игру (В), то игрок 2 пасует (П) или уравнивает игру (У);
V - выигрыш игрока 1 (проигрыш игрока 2).
Другой способ описания игры состоит в том, что рассматриваются все возможные стратегии каждого игрока и определяются платежи, соответствующие любой возможной комбинации стратегии всех игроков.
Описанная таким образом игра называется ИГРОЙ В НОРМАЛЬНОЙ ФОРМЕ. Нормальная форма игра двух участников может состоять из двух платежных матриц, показывающих, какую сумму получает каждый из игроков при любой из возможных пар стратегий. Обычно эти две матрицы выражают в форме единой матрицы, показанной на рис. 1.4.

 Элементами этой матрицы являются пара чисел, первое из которых определяет величину выигрыша игрока 1, второе- игрока 2. Игрок 1 (чаще называют игроком А) выбирает одну из n стратегий, обозначенных символами S11, S12,..., S1n; каждой стратегии соответствует строка матрицы. Игрок 2 (игрок В) выбирает одну из m стратегий S21, S22 ,…,S2m; каждой стратегии этого игрока соответствует столбец матрицы. Пара чисел на пересечении строки и столбца, которые соответствуют стратегиям, выбранным игроками, показывает величину выигрыша каждого из них. Например, если игрок 1 (игрок А) выбирает стратегию S1i (или Аi), а игрок 2 (игрок В) - S2j (или Вj), то выигрыши игроков 1 и 2 равны, соответственно, W1ij и W2ij (i= 1,n; j= 1,m).
Элементами этой матрицы являются пара чисел, первое из которых определяет величину выигрыша игрока 1, второе- игрока 2. Игрок 1 (чаще называют игроком А) выбирает одну из n стратегий, обозначенных символами S11, S12,..., S1n; каждой стратегии соответствует строка матрицы. Игрок 2 (игрок В) выбирает одну из m стратегий S21, S22 ,…,S2m; каждой стратегии этого игрока соответствует столбец матрицы. Пара чисел на пересечении строки и столбца, которые соответствуют стратегиям, выбранным игроками, показывает величину выигрыша каждого из них. Например, если игрок 1 (игрок А) выбирает стратегию S1i (или Аi), а игрок 2 (игрок В) - S2j (или Вj), то выигрыши игроков 1 и 2 равны, соответственно, W1ij и W2ij (i= 1,n; j= 1,m).
Стратегии игрока 2
Сратегии игрока 1 |
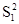 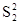 . . . . . . 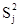 . . . . . . 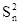
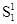 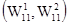 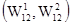 . . . . . . 
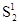 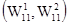 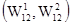 . . . . . .  .
. . . . .
.
.
. . . . .
.
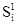 . . . . 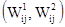 .
. .
. . . . .
. .
. .
. . . . .
.
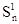 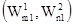 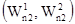 . . . . . . 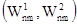
| |||||||||||
Рис. 1.4. Платежная матрица для игры двух участников.
Платежная матрица имеет размер n×m, где n - (конечное) число возможных стратегий игрока 1, m - (конечное) число возможных стратегий игрока 2. Предполагается, что каждому из игроков известны все элементы платежных матриц.
Игра называется ИГРОЙ С ПОЛНОЙ ИНФОРМАЦИЕЙ, если в ней нельзя делать одновременно несколько ходов и если результаты случайных ходов и предыдущих личных ходов полностью известны каждому игроку (игра в шашки, шахматы, в крестики-нолики). И, наоборот, игра называется ИГРОЙ С НЕПОЛНОЙ ИНФОРМАЦИЕЙ, если игрокам неизвестны некоторые выборы, сделанные при случайных ходах. Например, игра в покер, в которой, прежде всего, неизвестно какие карты находятся на руках у противника.
Дата добавления: 2018-09-22; просмотров: 204; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!


