Применение магнитного поля типа «магнитный кокон»
В биологии и медицине.
УДК 577.23, УДК 577.24
Медицина. {14.04.2017 03.00 МСК} Теория, требующая совершенно безопасной и относительно дешёвой экспериментальной проверки, предсказывает, что при помощи особой конфигурации такого магнитного поля, становится возможным лечить болезни суставов, кровеносную, лимфатическую и нервную системы организма за счёт глубинного эндофореза. Я, также, предполагаю, что в определённых условиях такое поле способно содействовать омоложению организма и значительному увеличению продолжительности жизни за счёт значительного продления молодости и зрелости. Известно, что живые организмы это коллоидные растворы с упорядоченным и целенаправленным движением материи (атомов и молекул, взаимодействующих при помощи электрического и магнитного полей) и информации с помощью энергетики. Об этом знают биофизики и специалисты в области информации. Так вот, при помощи такого поля, можно направленно управлять энергетикой и процессами, происходящими в организме на молекулярном и атомарном уровнях, а именно, сшивать повреждённые участки белков, РНК и ДНК и механизма, компенсирующего укорочение теломер (теломеразы).
Приложение 1
© Евгений Александрович Григорьев с помощью программы MathCad
Январь 1997 года
Впервые в науке - расчет магнитного поля внутри системы проводников,
эквивалентной по электромагнитным свойствам полому замкнутому проводнику.
Рассчитывается напряженность магнитного поля вдоль координатной оси X.
Поверхностный ток Is, текущий по полому замкнутому проводнику между его полюсами А и В, можно представить в виде "нитей тока" i [И.Е. Тамм, Основы теории электричества, стр. 140], токов, текущих по математическим меридианам сферы от B к А.
 Это значительно упрощает программу расчета магнитного поля внутри системы проводников, эквивалентной по электромагнитным свойствам (в необходимом приближении) сферическому полому замкнутому проводнику (ПЗП ).
Это значительно упрощает программу расчета магнитного поля внутри системы проводников, эквивалентной по электромагнитным свойствам (в необходимом приближении) сферическому полому замкнутому проводнику (ПЗП ).


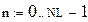
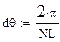



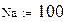






Закон Био-Савара-Лапласа
в векторной форме
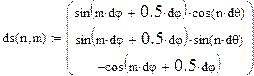

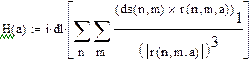

Видно, что в пределах точности машинного счёта, МП внутри ПЗП равно нулю.
Приложение 2
Программа расчёта интенсивности магнитного поля внутри сферического полого замкнутого проводника вдоль координаты Х на языке программирования Quick BASIC
1995 год
'SFERA
SCREEN 12
TIMER ON
LOCATE 12, 1
COLOR 15
PRINT "Calculation of a magnetostatic field inside a Spherical Conductors System, which";
LOCATE 14, 2
PRINT "is equivalent by electromagnetic properties to a Closed and Hollow Conductor."
ON TIMER(7) GOSUB 1
DO WHILE INKEY$ = "": LOOP
1
CLS
Nl = 150 'number of lines with current in Spherical Conductor System
Nds = 50 'number of elements of current in line of SCS
DIM SG(Nds + 1), CG(Nds + 1)
C$ = " +###.##"
Pi = 3.14159265359#
I = 10 'SCS line current
IL = I * Nl 'current of Linear Conductor
Ndl = Nds 'number of elements of current in Linear Conductor
Rs = 20
L = Rs 'length of Linear Conductor strength
dl = L / Ndl
dg = 2 * Pi / Nds
ds = Rs * dg
FOR j = 0 TO Nds - 1
SG(j) = SIN(j * dg + dg / 2)
CG(j) = COS(j * dg + dg / 2)
NEXT j
LINE (500, 10)-(500, 60), 9
LOCATE 3, 64
COLOR 9
PRINT "LC"
CIRCLE (500, 110), 50, 15
LINE (500, 110)-(550, 110), 8
LOCATE 7, 66
COLOR 8
PRINT "Rs"
COLOR 5
LINE (20, 40)-(320, 40) 'X-axis
LINE (20, 105)-(320, 105) 'Y-axis
LINE (20, 165)-(320, 165) 'Z-axis
LINE (20, 230)-(320, 230) 'SCS module-axis
LINE (20, 300)-(320, 300) 'Linear current module-axis
LINE (320, 10)-(320, 350), 8, , &HFF00
LOCATE 23, 40
COLOR 8
PRINT "Rs (radius of SCS,"
LOCATE 24, 30
PRINT "along which calculates a magnetic field)"
FOR X = 0 TO Rs - 1 STEP 1
HVx = 0
HVy = 0
HVz = 0
Hs = 0
HCx = 0
HCy = 0
HCz = 0
HL = 0
FOR v = 0 TO Nds - 1
HUx = 0
HUy = 0
HUz = 0
FOR u = 0 TO Nl - 1
Rx = X - Rs * SG(v) * COS(u)
Ry = -Rs * SG(v) * SIN(u)
Rz = -Rs * CG(v)
R3 = (SQR(Rx * Rx + Ry * Ry + Rz * Rz)) ^ 3
dsx = -ds * CG(v) * COS(u)
dsy = -ds * CG(v) * SIN(u)
dsz = ds * SG(v)
Hsx = (dsy * Rz - Ry * dsz) / R3
Hsy = (dsz * Rx - Rz * dsx) / R3
Hsz = (dsx * Ry - Rx * dsy) / R3
HUx = HUx + Hsx
HUy = HUy + Hsy
HUz = HUz + Hsz
NEXT u
HVx = HVx + HUx
HVy = HVy + HUy
HVz = HVz + HUz
Hs = SQR(HVx ^ 2 + HVy ^ 2 + HVz ^ 2)
RLx = X
'RLy = 0
RLz = Rs + dl * v + dl / 2
RL3 = (SQR(RLx * RLx + RLz * RLz)) ^ 3
'dlx = 0
'dly = 0
dlz = dl
'Hlx = (dly * RLz - RLy * dlz) / RL3
Hly = (dlz * RLx - RLz * dlx) / RL3
'Hlz = (dlx * RLy - RLx * dly) / RL3
'HCx = HCx + Hlx
HCy = HCy + Hly
'HCz = HCz + Hlz
'HL = SQR(HCx ^ 2 + HCy ^ 2 + HCz ^ 2)
HL = HCy
NEXT v
LOCATE 2, 1
COLOR 14
PRINT "Hsx ="; USING C$; I * HVx
PSET (X * 300 / Rs + 20, HVx + 40)
COLOR 10
LOCATE 6, 1
PRINT "Hsy ="; USING C$; I * HVy
PSET (X * 300 / Rs + 20, HVy + 105)
COLOR 11
LOCATE 10, 1
PRINT "Hsz ="; USING C$; I * HVz
PSET (X * 300 / Rs + 20, HVz + 165)
COLOR 15
LOCATE 14, 1
PRINT "Hs ="; USING C$; I * Hs
PSET (X * 300 / Rs + 20, Hs + 230)
LOCATE 14, 25
PRINT "Magnetic intensity in Spherical Conductors System (SCS)"
'LOCATE 14, 25
'PRINT "in Spherical Conductors System (SCS)"
COLOR 9
LOCATE 18, 1
PRINT "HL ="; USING C$; HL * IL * 10
PSET (X * 300 / Rs + 20, HL * IL * 10 + 300)
LOCATE 18, 25
PRINT "Magnetic intensity from Linear Conductor current (LC)"
NEXT X
FOR X = Rs TO Rs * 2 STEP 1
HCx = 0
HCy = 0
HCz = 0
HL = 0
FOR v = 0 TO Nds - 1
RLx = X
'RLy = 0
RLz = Rs + dl * v + dl / 2
RL3 = (SQR(RLx * RLx + RLz * RLz)) ^ 3
'dlx = 0
'dly = 0
dlz = dl
'Hlx = (dly * RLz - RLy * dlz) / RL3
Hly = (dlz * RLx - RLz * dlx) / RL3
'Hlz = (dlx * RLy - RLx * dly) / RL3
'HCx = HCx + Hlx
HCy = HCy + Hly
'HCz = HCz + Hlz
'HL = SQR(HCx ^ 2 + HCy ^ 2 + HCz ^ 2)
HL = HCy
NEXT v
PSET (X * 300 / Rs + 20, HL * IL * 10 + 300)
NEXT X
STOP
COLOR 15
END
Приложение 3
Движение одной заряженной частицы в магнитном поле, создаваемом двумя другими движущимися частицами и между ними.
SCREEN 12
TIMER ON
COLOR 3
LOCATE 2, 12
PRINT " Motion of one charged corpuscle (OMC)"
LOCATE 4, 12
PRINT " in a magnetic field (MF) such as a Magnetic; Cocoon,"
LOCATE 6, 12
PRINT "which is created by two others mobile charged corpuscles (TMC)"
LOCATE 8, 25
PRINT "Etmc = 5 eV; Eomc = 50 eV"
ON TIMER(5) GOSUB 1
DO WHILE INKEY$ = "": LOOP
1
CLS
C$ = " +#.#####^^^^"
Pi = 3.141593
Mo = 4 * Pi * .0000001
K = Mo / (4 * Pi) 'SI
M = 1.67E-27 * 2 '[kg]
Q = 1.6E-19 '[C]
LOCATE 6, 2
COLOR 9
INPUT "distance between TMC [sm](10 - 50)="; A0
a = A0 * .01 '[m] distance between TMC
Xk1 = 0
Yk1 = 0
Xk2 = Xk1 + a
Yk2 = 0
CIRCLE (Xk1 * 1000 + 50, Yk1 + 240), 10, 9
CIRCLE (Xk2 * 1000 + 50, Yk2 + 240), 10, 9
Ek = 5 '[eV] energy of TMC
TVk = 0 'angle of moving of TMC
Vk = SQR(2 * Ek * ABS(Q) / M) 'velocity of TMC
Vkx = Vk * COS(TVk)
Vky = 0
Vkz = 0
LOCATE 1, 60
PRINT "V tmc ="; USING C$; Vk
COLOR 13
Eq = 50 '[eV] energy of entry of OMC
LOCATE 8, 2
INPUT "angle of entry of OMC (0 - 360)="; TVq
Vq = SQR(2 * Eq * ABS(Q) / M) 'velocity of OMC
Vqx = Vq * COS(TVq)
Vqy = Vq * SIN(TVq)
Vqz = 0
LOCATE 3, 60
PRINT "V omc ="; USING C$; Vq
dlq = .0001# 'step of moving of OMC
Xq = Xk1 + .5 * a 'coordinate began movements of OMC
LOCATE 10, 2
INPUT "Coordinate Y began movements of OMC [sm](-25/+25)="; Yq0
COLOR 8
Yq = Yq0 * .01
Zq = 0
Fx = 0
Fy = 0
Fz = 0
FOR t = 0 TO 100000
dt = dlq / Vq
Rx1 = Xq - Xk1
Rx2 = Xq - Xk2
Ry1 = Yq - Yk1
Ry2 = Yq - Yk2 'Rz1 = 0 Rz2 = 0
R1 = SQR(Rx1 * Rx1 + Ry1 * Ry1)
R2 = SQR(Rx2 * Rx2 + Ry2 * Ry2)
'B = K * Q * [V x R] / R^3 MF, created by TMC [Tl]
'Љ—1
'Bx1 = K * Q * (Vky * Rz1 - Ry1 * Vkz) / R1 ^ 3 == 0
'By1 = K * Q * (Vkz * Rx1 - Rz1 * Vkx) / R1 ^ 3 == 0
Bz1 = K * Q * (Vkx * Ry1 - Rx1 * Vky) / R1 ^ 3
'Љ—2
'Bx2 = K * Q * (Vky * Rz2 - Ry2 * Vkz) / R2 ^ 3 == 0
'By2 = K * Q * (Vkz * Rx2 - Rz2 * Vkx) / R2 ^ 3 == 0
Bz2 = K * Q * (Vkx * Ry2 - Rx2 * Vky) / R2 ^ 3
'Lorentz force which influence on OMC FL = Q*[V x B]
'Px = (Vy * (Hz1 + Hz2) - (Hy1 + Hy2) * Vz)
'Py = (Vz * (Hx1 + Hx2) - (Hz1 + Hz2) * Vx)
'Pz = (Vx * (Hy1 + Hy2) - (Hx1 + Hx2) * Vy)
Fx = Vqy * (Bz1 + Bz2)
Fy = -(Bz1 + Bz2) * Vqx
'Fz = (Vqx * (By1 + By2) - (Bx1 + Bx2) * Vqy) ==0
'F = M*dV/dt = FL = Q*[V x Bk] ==> dV=PX*dt/M
dVqx = Fx * dt / M
dVqy = Fy * dt / M
dVqz = 0 'dVz = Fz * dt / M
Vqxt = Vqx + dVqx
Vqyt = Vqy + dVqy
Vqzt = 0 'Vqzt = Vqz + dVqz
Vqt = SQR(Vqxt ^ 2 + Vqyt ^ 2) '+ Vqzt ^ 2)
kV = Vq / Vqt
'kV - because velocity of OMC must be constant
Vqx = Vqxt * kV
Vqy = Vqyt * kV
Vqz = 0 'Vqz = Vqzt * kV
V = SQR(Vqx ^ 2 + Vqy ^ 2) '+ Vqz ^ 2)
dXq = Vqx * dt
dYq = Vqy * dt
dZq = 0 'dZq = Vz * dt
Xq = Xq + dXq
Yq = Yq + dYq
Zq = 0 'Zq = Zq + dZq
PSET (Xq * 1000 + 50, Yq * 1000 + 240), 13
NEXT t
END
Приложение 4
Движение заряженной частицы в магнитном поле типа «Магнитный кокон».
SCREEN 12
TIMER ON
COLOR 3
LOCATE 3, 17
PRINT " Motion of one deuteron in a magnetic field "
LOCATE 5, 17
PRINT " such as a Magnetic Cocoon "
LOCATE 7, 17
PRINT " Ed = 500 eV"
COLOR 15
ON TIMER(3) Gosub 1
DO While INKEY$ = "": LOOP
1
CLS
Dim X1(80), X2(80)
C$ = " +#.#####^^^^"
Pi = 3.141593
Mo = 4 * Pi * .0000001
M = 1.67E-27 * 2
Q = 1.6E-19
E = 500 '[eV]
2 CLS
LOCATE 2, 10
INPUT "ANGLE (50 - 175)="; AN
If 175 < AN Goto 2
If AN < 50 Goto 2
TV = AN * Pi / 180
V = Sqr(2 * E * Abs(Q) / M)
Vx = V * Cos(TV)
Vy = V * Sin(TV)
Vz = 0
LOCATE 2, 60
PRINT "V ="; USING C$; V
dlq = .0002
'dt = dlq / V
A = .04
YL1 = 0
YL2 = 0
Xv = 0
Yv = .001
Zv = 0
L = .08
DL = .001
N = L / DL
IL = 3000000
K = Mo / (4 * Pi)
For I = 0 To N - 1
X1(I) = -I * DL - DL / 2 - A
X2(I) = I * DL + DL / 2 + A
Next I
For t = 0 To 3000
dt = dlq / V
PXx = 0
PXy = 0
PXz = 0
For I = 0 To N - 1
Rx1 = Xv - X1(I)
Rx2 = Xv - X2(I)
Ux = DL
Uy = 0
Uz = 0
Ry1 = Yv + YL1
Ry2 = Yv + YL2
Rz = Zv
R1 = Sqr(Rx1 * Rx1 + Ry1 * Ry1 + Rz * Rz)
R2 = Sqr(Rx2 * Rx2 + Ry2 * Ry2 + Rz * Rz)
Hy1 = (-Rz * Ux) / R1 ^ 3
Hz1 = (Ux * Ry1) / R1 ^ 3
Hy2 = (-Rz * Ux) / R2 ^ 3
Hz2 = (Ux * Ry2) / R2 ^ 3
Px = (Vy * (Hz1 + Hz2) - (Hy1 + Hy2) * Vz)
Py = -(Hz1 + Hz2) * Vx
Pz = Vx * (Hy1 + Hy2)
PXx = PXx + Px
PXy = PXy + Py
PXz = PXz + Pz
Next I
dVx = Q * K * IL * PXx * dt / M
dVy = Q * K * IL * PXy * dt / M
dVz = Q * K * IL * PXz * dt / M
Vxt = Vx + dVx
Vyt = Vy + dVy
Vzt = Vz + dVz
Vt = Sqr(Vxt ^ 2 + Vyt ^ 2 + Vzt ^ 2)
kV = V / Vt
'kV - the particle must have a constant value modulo of velocity
Vx = Vxt * kV
Vy = Vyt * kV
Vz = Vzt * kV
V = Sqr(Vx ^ 2 + Vy ^ 2 + Vz ^ 2)
dXv = Vx * dt
dYv = Vy * dt
dZv = Vz * dt
Xv = Xv + dXv
Yv = Yv + dYv
Zv = Zv + dZv
PSET (Xv * 10000 + 320, Yv * 10000 + 240), 12
Next t
End
Приложение 5
Движение двух заряженных частиц в магнитном поле типа «Магнитный кокон» с учётом Кулоновского взаимодействия.
SCREEN 12
TIMER ON
COLOR 3
LOCATE 3, 17
PRINT " Motion of two deuterones in a magnetic field "
LOCATE 5, 17
PRINT " such as a Magnetic Cocoon "
COLOR 15
ON TIMER(3) GOSUB 1
DO WHILE INKEY$ = "": LOOP
1
CLS
DIM XP1(150), XP2(150)
C$ = " #.###^^^^"
Pi = 3.141593
Eo = 8.85E-12
Mo = 4 * Pi * .0000001
M = 1.67E-27 * 2
Q = 1.6E-19
E = 700! '[eV]
J = 8E+08
LOCATE 3, 10
INPUT "ANGLE (30 - 170)="; AN
IF 170 < AN GOTO 1
IF AN < 30 GOTO 1
TV = AN * Pi / 180
V = SQR(2 * E * ABS(Q) / M)
Vx1 = V * COS(TV)
Vy1 = V * SIN(TV)
Vz1 = 0
Vx2 = Vx1
Vy2 = -Vy1
dlq = .0001
A = .007
Xv1 = 0
Yv1 = .0003
Xv2 = 0
Yv2 = -.0003
L = .25
DL = .01
N = L / DL
Du = .06
S = Pi * Du ^ 2 / 4
IL = S * J
K = Mo / (4 * Pi)
FOR I = 0 TO N - 1
XP1(I) = -I * DL - DL / 2 - A
XP2(I) = I * DL + DL / 2 + A
NEXT I
FOR t = 0 TO 8000
IL = S * J
K1 = 5000000!
dt = dlq / V
LOCATE 2, 65
PRINT "t ="; USING C$; t * dt
PXx1 = 0
PXy1 = 0
PXx2 = 0
PXy2 = 0
PCx1 = 0
PCy1 = 0
PCx2 = 0
PCy2 = 0
FOR I = 0 TO N - 1
Rx11 = Xv1 - XP1(I)
Rx12 = Xv1 - XP2(I)
Rx21 = Xv2 - XP1(I)
Rx22 = Xv2 - XP2(I)
Ux = DL
REM Uy = 0 Uz = 0
Ry1 = Yv1
Ry2 = Yv2
R11 = SQR(Rx11 * Rx11 + Ry1 * Ry1)
R12 = SQR(Rx12 * Rx12 + Ry1 * Ry1)
R21 = SQR(Rx21 * Rx21 + Ry2 * Ry2)
R22 = SQR(Rx22 * Rx22 + Ry2 * Ry2)
RGx1 = Xv1 - Xv2
RGy1 = Yv1 - Yv2
RG1 = SQR(RGx1 ^ 2 + RGy1 ^ 2)
RGx2 = -RGx1
RGy2 = -RGy1
RG2 = RG1
REM Hx1 = (Uy * Rz - Ry * Uz) / R1 ^ 3
REM Hy1 = (Uz * Rx1 - Rz * Ux) / R1 ^ 3
REM Hz1 = (Ux * Ry - Rx1 * Uy) / R1 ^ 3
Hz11 = (Ux * Ry1) / R11 ^ 3
Hz12 = (Ux * Ry1) / R12 ^ 3
Hz21 = (Ux * Ry2) / R21 ^ 3
Hz22 = (Ux * Ry2) / R22 ^ 3
REM Px = (Vy * (Hz1 + Hz2) - (Hy1 + Hy2) * Vz)
REM Py = (Vz * (Hx1 + Hx2) - (Hz1 + Hz2) * Vx)
REM Pz = (Vx * (Hy1 + Hy2) - (Hx1 + Hx2) * Vy)
PGx1 = RGx1 / (ABS(RG1 ^ 3)) * K1
PGy1 = RGy1 / (ABS(RG1 ^ 3)) * K1
PGx2 = RGx2 / (ABS(RG2 ^ 3)) * K1
PGy2 = RGy2 / (ABS(RG2 ^ 3)) * K1
'Coefficient "K1" imitates group of particles
Px1 = Vy1 * (Hz11 + Hz12)
Py1 = -(Hz11 + Hz12) * Vx1
Px2 = Vy2 * (Hz21 + Hz22)
Py2 = -(Hz21 + Hz22) * Vx2
PCx1 = PCx1 + PGx1
PCy1 = PCy1 + PGy1
PCx2 = PCx2 + PGx2
PCy2 = PCy2 + PGy2
PXx1 = PXx1 + Px1
PXy1 = PXy1 + Py1
PXx2 = PXx2 + Px2
PXy2 = PXy2 + Py2
NEXT I
dVx1 = Q * K * IL * PXx1 * dt / M
dVy1 = Q * K * IL * PXy1 * dt / M
dVx2 = Q * K * IL * PXx2 * dt / M
dVy2 = Q * K * IL * PXy2 * dt / M
Vxt1 = Vx1 + dVx1
Vyt1 = Vy1 + dVy1
Vt1 = SQR(Vxt1 ^ 2 + Vyt1 ^ 2)
kV1 = V / Vt1
Vxt2 = Vx2 + dVx2
Vyt2 = Vy2 + dVy2
Vt2 = SQR(Vxt2 ^ 2 + Vyt2 ^ 2)
kV2 = V / Vt2
'kV - the particle must have a constant value modulo of velocity
dVCx1 = Q ^ 2 * PCx1 * dt / M / (4 * Pi * Eo)
dVCy1 = Q ^ 2 * PCy1 * dt / M / (4 * Pi * Eo)
dVCx2 = Q ^ 2 * PCx2 * dt / M / (4 * Pi * Eo)
dVCy2 = Q ^ 2 * PCy2 * dt / M / (4 * Pi * Eo)
Vx1 = Vxt1 * kV1 + dVCx1
Vy1 = Vyt1 * kV1 + dVCy1
Vx2 = Vxt2 * kV2 + dVCx2
Vy2 = Vyt2 * kV2 + dVCy2
Vt = SQR(Vx1 ^ 2 + Vy1 ^ 2 + Vz1 ^ 2)
REM LOCATE 23, 20
REM PRINT "Vt ="; USING C$; Vt
dXv1 = Vx1 * dt
dYv1 = Vy1 * dt
dXv2 = Vx2 * dt
dYv2 = Vy2 * dt
Xv1 = Xv1 + dXv1
Yv1 = Yv1 + dYv1
Xv2 = Xv2 + dXv2
Yv2 = Yv2 + dYv2
PSET (Xv1 * 70000 + 320, Yv1 * 60000 + 240), 9
PSET (Xv2 * 70000 + 320, Yv2 * 60000 + 240), 12
IF t = 2000 THEN CLS 1
IF t = 5000 THEN CLS 1
IF t = 6500 THEN CLS 1
NEXT t
LOCATE 29, 5
INPUT "repeat under other angle - 1 "; U1
IF U1 = 1 THEN GOTO 1
IF U1 <> 1 THEN END
Приложение 6
Движение двух заряженных частиц в нарастающем магнитном поле типа «Магнитный кокон» - «Сферический пинч».
SCREEN 12
TIMER ON
COLOR 3
LOCATE 3, 12
PRINT " Motion of two deuterones"
LOCATE 5, 12
PRINT " in a increasing magnetic field such as a Magnetic Cocoon "
LOCATE 7, 12
PRINT " (Spherical pinch)"
COLOR 15
ON TIMER(4) GOSUB 1
DO WHILE INKEY$ = "": LOOP
1
CLS
DIM XP1(80), XP2(80)
C$ = " ##.###^^^^"
Pi = 3.141593
Eo = 8.85E-12
Mo = 4 * Pi * .0000001
M = 1.67E-27 * 2
Q = 1.6E-19
E = 10000 '[eV]
J = 7E+10
LOCATE 2, 10
INPUT "ANGLE (60 - 300)="; AN
IF 300 < AN GOTO 1
IF AN < 60 GOTO 1
TV = AN * Pi / 180
V = SQR(2 * E * ABS(Q) / M)
Vx1 = V * COS(TV)
Vy1 = V * SIN(TV)
Vz1 = 0
Vx2 = Vx1
Vy2 = -Vy1
dlq = .0003
A = .015
Xv1 = 0
Yv1 = .001
Xv2 = 0
Yv2 = -.001
L = .08
DL = .001
N = L / DL
Du = .01
s = Pi * Du ^ 2 / 4
IL = s * J
K = Mo / (4 * Pi)
FOR i = 0 TO N - 1
XP1(i) = -i * DL - DL / 2 - A
XP2(i) = i * DL + DL / 2 + A
'PSET ((XP1(I) * 2000 + 320 - A * 5000), 240)
'PSET ((XP2(I) * 2000 + 320 + A * 5000), 240)
NEXT i
tt = 0
FOR t = 0 TO 8000
dt = dlq / V
tt = tt + dt
LOCATE 2, 65
PRINT "t ="; USING C$; tt
LOCATE 4, 65
PRINT "I ="; USING C$; IL
PXx1 = 0
PXy1 = 0
PXx2 = 0
PXy2 = 0
PCx1 = 0
PCy1 = 0
PCx2 = 0
PCy2 = 0
FOR i = 0 TO N - 1
Rx11 = Xv1 - XP1(i)
Rx12 = Xv1 - XP2(i)
Rx21 = Xv2 - XP1(i)
Rx22 = Xv2 - XP2(i)
Ux = DL
REM Uy = 0 Uz = 0
Ry1 = Yv1
Ry2 = Yv2
R11 = SQR(Rx11 * Rx11 + Ry1 * Ry1)
R12 = SQR(Rx12 * Rx12 + Ry1 * Ry1)
R21 = SQR(Rx21 * Rx21 + Ry2 * Ry2)
R22 = SQR(Rx22 * Rx22 + Ry2 * Ry2)
RGx1 = Xv1 - Xv2
RGy1 = Yv1 - Yv2
RG1 = SQR(RGx1 ^ 2 + RGy1 ^ 2)
RGx2 = -RGx1
RGy2 = -RGy1
RG2 = RG1
REM Hx1 = (Uy * Rz - Ry * Uz) / R1 ^ 3
REM Hy1 = (Uz * Rx1 - Rz * Ux) / R1 ^ 3
REM Hz1 = (Ux * Ry - Rx1 * Uy) / R1 ^ 3
Hz11 = (Ux * Ry1) / R11 ^ 3
Hz12 = (Ux * Ry1) / R12 ^ 3
Hz21 = (Ux * Ry2) / R21 ^ 3
Hz22 = (Ux * Ry2) / R22 ^ 3
REM Px = (Vy * (Hz1 + Hz2) - (Hy1 + Hy2) * Vz)
REM Py = (Vz * (Hx1 + Hx2) - (Hz1 + Hz2) * Vx)
REM Pz = (Vx * (Hy1 + Hy2) - (Hx1 + Hx2) * Vy)
PGx1 = RGx1 / (ABS(RG1 ^ 3))
PGy1 = RGy1 / (ABS(RG1 ^ 3))
PGx2 = RGx2 / (ABS(RG2 ^ 3))
PGy2 = RGy2 / (ABS(RG2 ^ 3))
Px1 = Vy1 * (Hz11 + Hz12)
Py1 = -(Hz11 + Hz12) * Vx1
Px2 = Vy2 * (Hz21 + Hz22)
Py2 = -(Hz21 + Hz22) * Vx2
PCx1 = PCx1 + PGx1
PCy1 = PCy1 + PGy1
PCx2 = PCx2 + PGx2
PCy2 = PCy2 + PGy2
PXx1 = PXx1 + Px1
PXy1 = PXy1 + Py1
PXx2 = PXx2 + Px2
PXy2 = PXy2 + Py2
NEXT i
dVx1 = Q * K * IL * PXx1 * dt / M
dVy1 = Q * K * IL * PXy1 * dt / M
dVx2 = Q * K * IL * PXx2 * dt / M
dVy2 = Q * K * IL * PXy2 * dt / M
Vxt1 = Vx1 + dVx1
Vyt1 = Vy1 + dVy1
Vt1 = SQR(Vxt1 ^ 2 + Vyt1 ^ 2)
kV1 = V / Vt1
Vxt2 = Vx2 + dVx2
Vyt2 = Vy2 + dVy2
Vt2 = SQR(Vxt2 ^ 2 + Vyt2 ^ 2)
kV2 = V / Vt2
'kV - the particle must have a constant value modulo of velocity
kq = 3000 'Magnification of distance of a Coulomb interaction
'imitates group of particles
dVCx1 = (kq * Q) ^ 2 * PCx1 * dt / M / (4 * Pi * Eo)
dVCy1 = (kq * Q) ^ 2 * PCy1 * dt / M / (4 * Pi * Eo)
dVCx2 = (kq * Q) ^ 2 * PCx2 * dt / M / (4 * Pi * Eo)
dVCy2 = (kq * Q) ^ 2 * PCy2 * dt / M / (4 * Pi * Eo)
Vx1 = Vxt1 * kV1 + dVCx1
Vy1 = Vyt1 * kV1 + dVCy1
Vx2 = Vxt2 * kV2 + dVCx2
Vy2 = Vyt2 * kV2 + dVCy2
Vt = SQR(Vx1 ^ 2 + Vy1 ^ 2 + Vz1 ^ 2)
REM LOCATE 23, 20
REM PRINT "Vt ="; USING C$; Vt
dXv1 = Vx1 * dt
dYv1 = Vy1 * dt
dXv2 = Vx2 * dt
dYv2 = Vy2 * dt
Xv1 = Xv1 + dXv1
Yv1 = Yv1 + dYv1
Xv2 = Xv2 + dXv2
Yv2 = Yv2 + dYv2
PSET (Xv1 * 25000 + 320, Yv1 * 25000 + 240), 9
PSET (Xv2 * 25000 + 320, Yv2 * 25000 + 240), 4
Y12 = Yv1 - Yv2
IF Y12 < .0000000000002# THEN dlq = .00000000000001#
IF Y12 > .0000000000002# THEN dlq = .00000000000002#
IF Y12 > .000000000002# THEN dlq = .0000000000002#
IF Y12 > .00000000002# THEN dlq = .000000000002#
IF Y12 > .0000000002# THEN dlq = .00000000002#
IF Y12 > .000000002# THEN dlq = .0000000002#
IF Y12 > .00000002# THEN dlq = .000000002#
IF Y12 > .0000002# THEN dlq = .00000002#
IF Y12 > .000002 THEN dlq = .0000002#
IF Y12 > .00002 THEN dlq = .000004#
IF Y12 > .0002 THEN dlq = .00004#
IF Y12 > .002 THEN dlq = .0001#
IF t = 7000 THEN CLS 1
J = J + 8E+07
IL = s * J
NEXT t
LOCATE 29, 5
INPUT "Repeat with other angle - 1 "; U1
IF U1 = 1 THEN GOTO 1
IF U1 <> 1 THEN END
Приложение 7
Движение электрона в магнитном поле тора с полоидальным током – «Ондулятор».
SCREEN 12
COLOR 3
LOCATE 5, 5
PRINT " Motion of an electron in a magnetic field "
LOCATE 7, 5
PRINT " such as a Magnetic Cocoon (undulator) "
COLOR 15
C$ = " +#.#####^^^^"
Pi = 3.14159265359#
M = 9.1E-31
Q = 1.6E-19
jc = 6E+08
dt = 3E-10
Uq = 400!
Du = .001
TV = 30 * Pi / 180
K = 4 * Pi * .0000001 * (-Q) * (jc * Du ^ 2 / 4) / (4 * Pi)
V = SQR(2 * Q * Uq / M)
Vx = V * COS(TV)
Vy = V * SIN(TV)
Vz = 0
LOCATE 3, 60
PRINT "V= "; USING C$; V
A = .03
X1 = -.05
X2 = .05
dX = (X2 - X1) / 100
dG = Pi / 50
Xv = -.32
Yv = 0
Zv = 0
PSET (Xv * 1200 + 420, Yv * 4000 + 300)
DIM X(100)
FOR i = 0 TO 99
X(i) = X1 + i * dX + dX / 2
PSET (X(i) * 1200 + 420, A * 4000 + 300)
PSET (X(i) * 1200 + 420, -A * 4000 + 300)
NEXT i
PGx = 0
PGy = 0
PGz = 0
FOR t = 1 TO 100
FOR j = 0 TO 99
CG = COS(j * dG)
SG = SIN(j * dG)
PXx = 0
PXy = 0
PXz = 0
Ry = -A * CG + Yv
Rz = -A * SG + Zv
Ry2 = Ry * Ry
Rz2 = Rz * Rz
Ux = dX 'Uy = 0 Uz = 0
FOR i = 0 TO 99
Rx = -X(i) + Xv 'R = SQR(Rx * Rx + Ry2 + Rz2)
R3 = (SQR(Rx * Rx + Ry2 + Rz2)) ^ 3
Hx = (Vy * Rz - Vz * Ry) / R3
Hy = (Vz * Rx - Vx * Rz) / R3
Hz = (Vx * Ry - Vy * Rx) / R3
'Px = Uy * Hz - Uz * Hy
Py = -Ux * Hz 'Py = Uz * Hx - Ux * Hz
Pz = Ux * Hy 'Pz = Ux * Hy - Uy * Hx
'PXx = PXx + Px
PXy = PXy - Py
PXz = PXz - Pz
NEXT i
'PGx = PGx + PXx
PGy = PGy + PXy
PGz = PGz + PXz
NEXT j
'dVx = K * PGx * dt / M
dVy = K * PGy * dt / M
dVz = K * PGz * dt / M
Vxt = Vx + dVx
Vyt = Vy + dVy
Vzt = Vz + dVz
Vt = SQR(Vxt ^ 2 + Vyt ^ 2 + Vzt ^ 2)
kV = V / Vt
'kV - the particle must have a constant value modulo of velocity
Vx = Vxt * kV
Vy = Vyt * kV
Vz = Vzt * kV
V = SQR(Vx ^ 2 + Vy ^ 2 + Vz ^ 2)
dXv = Vx * dt
dYv = Vy * dt
dZv = Vz * dt
Xv = Xv + dXv
Yv = Yv + dYv
Zv = Zv + dZv
PSET (Xv * 1200 + 420, Yv * 4000 + 300), 12
NEXT t
Приложение 8
© Григорьев Евгений Александрович. 2004 год.
Дата добавления: 2018-09-20; просмотров: 365; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
