К СИСТЕМЕ УРАВНЕНИЙ МАКСВЕЛЛА.

Код УДК 537.8, УДК 537.5

О ЦИРКУЛЯЦИИ ВЕКТОРА НАПРЯЖЕННОСТИ МАГНИТНОГО ПОЛЯ.

Показана недостаточность теоремы о циркуляции вектора напряженности магнитного поля

в электрических цепях, включающих полый замкнутый проводник.

О том, что это добросовестное научное заблуждение, которое привело к интересным результатам,

будет сказано далее.

Показан ход научной мысли и логика рассуждений

Известно, что закон Ампера, под которым мировая наука понимает закон полного тока, появился как результат большого числа тщательных экспериментов с различными конфигурациями электрических цепей постоянного тока. Эти эксперименты объединяло одно - все цепи были линейными - только в них контур, по которому рассчитывается циркуляция вектора напряженности магнитного поля либо охватывает проводник, либо нет. Ампер тоже работал с линейными электрическими цепями. В то время, когда формулировался закон полного тока (закон Ампера), отсутствовала возможность численного расчета магнитного поля внутри полого замкнутого проводника (ПЗП), поля, создаваемого текущим по поверхности ПЗП и между его полюсами током. Аналитическое выражение такого векторного поля содержит эллиптический интеграл второго рода и, поэтому, не может быть приведено к элементарному виду для простых численных расчетов. Теоретики, со вполне обоснованной осторожностью, рассматривали только линейные контуры с током. Д. К. Максвелл, занимавшийся разработкой теории переменных полей, принял закон Ампера, как очевидную аксиому и только дополнил его уравнение током смещения. Хотя сам Максвелл отмечал, что полученная им система уравнений не является полной и что она неприменима, например, для случая незамкнутых токов, отрезков тока и отдельных элементов тока.

Тем не менее, постепенно, закон Ампера, в его изначальной формулировке, был принят, как норма, а теорема о циркуляции вектора напряженности МП стала, со временем, научной догмой. Из-за безоговорочного авторитета основоположников электромагнетизма и электродинамики и их, не менее знаменитых последователей и толкователей, другие токовые системы в дальнейшем не просчитывались, что значительно затормозило развитие теории и вытекающих из нее прикладных знаний. Наступило время заполнить этот пробел в электродинамике.

Начнем с азов и очевидного.

Рис. 1

Невозможно создать отдельный, незамкнутый отрезок проводника, в котором течет постоянный ток - это нарушает закон сохранения заряда (Рис.1). Поэтому кажется очевидным, что невозможно создать постоянное магнитное поле (МП) посредством отдельного элемента постоянного тока [1, с.163]. Логика этого вывода проста - нет объекта для рассмотрения. Таким образом, приравниваются понятия “отдельный, незамкнутый отрезок проводника” и “отдельный элемент замкнутого тока”. На основании этой логики интерпретируются известные экспериментальные факты и сделаны выводы в теории электромагнетизма.

Проверим полноту этой логики.

Будем рассматривать только электрические цепи постоянного тока. Терминология:

1) Проводник - тело, в котором есть движение зарядов, т.е. электрический ток, если внутри проводника напряженность электрического поля Е отлична от нуля. [1, с.26].

2) Закон обратных квадратов. Это закон о центральных полях создаваемых центрами сил (гравитационные массы, электрические заряды, магнитные полюсы) по закону обратной пропорциональности квадрату расстояния. Говорится об одинаковом описании таких полей [1,с.19], [1, с.46]. Известно, что тело, находящееся внутри гравитирующей полой сферы, силы тяготения не испытывает.

3) В пространстве, окружающем произвольный ток, всегда есть МП [1, с.161].

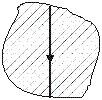
4) Замкнутый проводник (ЗП) - тело, обеспечивающее протекание тока по замкнутому линейному контуру [1, с.164, с.167]. Обычно этот контур неразветвленный. Контур выполнен из линейного, металлического проводника. Ток, текущий по ЗП, создает МП во всем окружающем пространстве (см. п.3).

5) Закон Био-Савара в векторной форме: 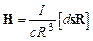[1, с. 163];

I - сила тока в проводнике; ds - элемент линейного проводника; R - расстояние от элемента тока Ids, создающего МП, до точки, где наблюдается напряженность H этого МП.

6) Полый замкнутый проводник (ПЗП) - проводящее тело. Оно сделано в виде неразрывной замкнутой поверхности, которая полностью охватывает некоторый объем [2, с.65]. Обычно, это поверхность тела вращения - цилиндрическая или сферическая. Точки пересечения поверхности и оси симметрии - полюса. Ток, текущий по ПЗП между полюсами, не создает МП в объеме, который он обтекает, а более точно - векторная сумма магнитных полей, создаваемых всеми элементами этого тока, в любой точке внутри ПЗП равна нулю, то есть, применяется принцип полной компенсации, основанный на не вызывающем сомнений принципе суперпозиции и широко используемый в различных измерительных и экспериментальных методиках.

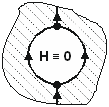
Это свойство ПЗП вытекает из законов Био-Савара и “обратных квадратов” (см. п.2, п.5). Иначе следует предположить, что напряженность МП, возбуждаемого элементом тока, изменяется по закону отличному от закона обратной пропорциональности квадрату расстояния, а это противоречит опыту.

То же самое подтверждается численными расчётами (Приложение 1, Приложение 2).

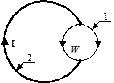
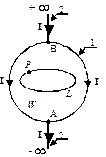
Рис. 2 Рис. 3 Рис. 4

Итак, в замкнутой электрической цепи с током могут существовать проводящие участки двух типов:

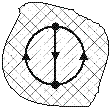
2) создающие МП везде; 1) не создающие МП внекотором объеме ( W ).

Минимальное количество участков обоих типов, нужных для создания замкнутой электрической цепи - два (Рис. 2, Рис. 3). На рисунках обозначены: 1 - ПЗП; 2- линейный проводник; I - ток, текущий в цепи; W - объем, охватываемый ПЗП.

Проанализируем цепь, показанную на Рис. 2.

Обозначим полюса ПЗП как А и В (Рис. 4). Линейный проводник 2, представим в виде полубесконечных прямолинейных отрезков -¥А и +¥В. Созданная цепь с током имеет осевую симметрию. При этом силовые линии МП имеют исключительно азимутальную (тангенциальную) компоненту. Они являются окружностями с центром на оси системы. Рассмотрим точку P. Она принадлежит контуру L. Контур L находится в объеме W и совпадает с предполагаемой, пока, силовой линией. ПЗП охватывает объем W.

Найдем циркуляцию вектора напряженности МП по контуру L. По определению: “Если кривая L замкнута, что отмечается кружком у знака интеграла, то линейный интеграл вектора а вдоль нее называется циркуляцией а вдоль L: 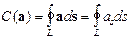(23*) ” [1, с.469]. В дальнейшем, элемент контура L будем обозначать dl, а элемент тока ds. Так как в нашем случае вектор H всегда параллелен dl, то: .

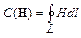Согласно принципу суперпозиции для цепи с током: “ ... напряженность поля H замкнутого тока I в произвольной точке P равна сумме полей, возбуждаемых каждым из его элементов, т.е. равна: 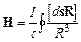(42.4) ” [1, с. 164]. В этом выражении подразумевается, что ток течет по линейному замкнутому контуру, по которому происходит интегрирование. Однако, в рассматриваемом случае, ток, который течет по ПЗП 1, не создает МП в объеме W (см. п.6) и формула (42.4) будет выглядеть так: 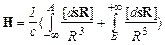, а циркуляция вектора напряженности магнитного поля по замкнутой кривой L .

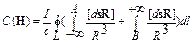Очевидно, что в рассматриваемой цепи циркуляция вектора напряженности магнитного поля по замкнутой кривой L , не охватывающей токов, не равна нулю, а предполагаемая силовая линия оказалась реальной. Это противоречит теореме о циркуляции вектора напряженности МП, в которой говорится о том, что: “ ...циркуляция вектора напряженности магнитного поля по кривой, не охватывающей токов, равна нулю... ” [1, с.178].

Откуда это противоречие? Попробуем разобраться.

Теорема Стокса.

“ Циркуляция произвольного вектора а по замкнутой кривой L равна потоку ротора этого вектора через поверхность S , опирающуюся на кривую L

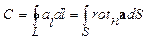” [1, с.472].

Была выведена формула: “ 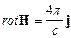(47.3) ” [1, с.177].

Теорема Стокса – чисто математическая, в ней нет ни слова о потоке зарядов через поверхность S – зарядов, создающих поток ротора. Тем не менее, утверждается: “На основании теоремы Стокса и уравнения (47.3) мы можем записать: 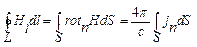(47.4) ” [1. с.177]. Очевидно, что происходит прямая подмена ротора вектора на ток, т. е. на вектор, который образует этот самый ротор. Это - следствие той самой, “очевидной” логики рассуждений.

Можно сделать вывод, что уравнение (47.3), в данном случае, неверно и требует теоретической доработки, а “... полная система дифференциальных уравнений магнитного поля постоянных токов...” [1. с.182] не является полной, как и система уравнений Максвелла (не всегда 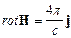). Это произошло потому, что рассматривались только линейные контуры с током. Более точно теорема о циркуляции вектора напряженности МП, создаваемого произвольным током должна выглядеть так: “Циркуляция вектора напряженности МП произвольного тока по произвольной замкнутой кривой L равна алгебраической сумме циркуляций элементов этого тока по этой кривой”.

Тем не менее, теорема о циркуляции вектора напряженности МП стала научной догмой. Из-за этого другие токовые системы в дальнейшем не просчитывались.

Кратко повторим логику вывода.

1) Или есть два типа проводников (1 - создающие МП во всем окружающем пространстве;

2 - создающие МП во всем окружающем пространстве за исключением части пространства, которую они охватывают;) – или неверны законы Био-Савара и обратных квадратов.

2) Или есть замкнутые цепи постоянного тока, где циркуляция вектора напряженности магнитного поля по замкнутой кривой L, не охватывающей токов, не равна нулю – или неверен принцип суперпозиции.

Рассмотрим последствия этих рассуждений.

Во-первых, нужно исключить бесконечность из формул и создать реальную физическую систему. Создадим осесимметричную замкнутую цепь (Рис.5), состоящую из двух линейных проводников AC, BD и двух сферических ПЗП 1 и 2, вложенных один в другой и не касающихся друг друга. Линейный проводник BD соединяет верхние полюса ПЗП 1 и 2. Линейный проводник AС соединяет нижние полюса ПЗП 1 и 2. Стрелками показано направление токов в цепи. Теперь формула (42.4) будет выглядеть так: 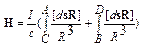, а циркуляция вектора напряженности МП по контуру L будет: 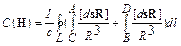, так как ПЗП 1 и 2 не создают МП в объеме W (см. п.6). Очевидно, что МП в объеме W есть сумма МП отдельных отрезков цепи - A C и B D.

Такое МП имеет следующие особенности (Рис.6, 7, 8):

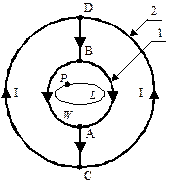
Рис. 5 Рис. 6

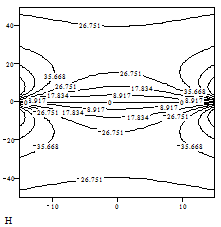
Структура магнитного поля в плоскости, содержащей ось симметрии в виде графика Кантора.

Показаны сечения поверхностей уровня равной напряженности МП.

Вектор напряженности направлен перпендикулярно плоскости рисунка.

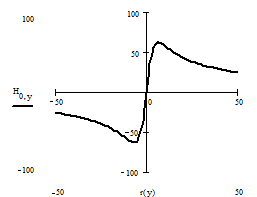
Рис. 7

Зависимость напряженности МП от расстояния до оси системы в плоскости Z = 0.

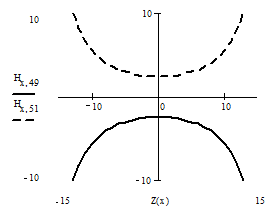
Рис. 8

Зависимость напряженности МП от координаты Z вдоль прямой, параллельной оси Z

и находящейся от оси на расстоянии ± dR.

1) линию нулевой напряженности поля (ЛНН);

2) минимум напряженности по трем координатам в центре системы (исключая ЛНН);

3) градиент такой, что напряженность поля возрастает по направлению из центра кривизны силовых линий.

Дата добавления: 2018-09-20; просмотров: 248; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 123 4 5 6 7 8 Следующая ⇒

Мы поможем в написании ваших работ!