Геометрическая интерпретация в случае двух переменных
|

Отыскание начального опорного плана (1 пункт алгоритма)
Пусть система ограничений ЗЛП представлена в канонической форме записи.
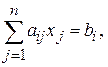

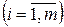 .
.
Говорят, что ограничение ЗЛП имеет предпочтительный вид, если при неотрицательности правой части (  ) левая часть ограничения содержит переменную, входящую с коэффициентом, равным единице, а в остальные ограничения-равенства - с коэффициентом, равным нулю.
) левая часть ограничения содержит переменную, входящую с коэффициентом, равным единице, а в остальные ограничения-равенства - с коэффициентом, равным нулю.
Например, в системе ограничений:
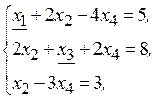
первое и второе ограничения имеют предпочтительный вид, а третье - нет (предпочтительные переменные подчеркнуты).
Если каждое ограничение системы имеет предпочтительный вид, то система представлена в предпочтительном виде. В этом случае легко найти ее опорное решение. Предпочтительные переменные будут базисными, а остальные - свободными. Все свободные переменные нужно приравнять к нулю, тогда базисные переменные будут равны свободным членам.
Например, в системе ограничений:
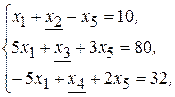
предпочтительными (базисными) являются переменные 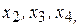 свободными являются переменные
свободными являются переменные 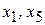 .
.
Приравниваем свободные переменные  к нулю, тогда базисные переменные примут значения:
к нулю, тогда базисные переменные примут значения: 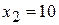 ,
,  ,
,  .
.
Получим начальный опорный план 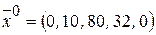 .
.
Отыскание начального опорного плана
Методом искусственного базиса
В случае, когда ограничение - равенство не имеет предпочтительного вида, к его левой части добавляют искусственную переменную 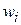
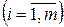 . В целевую функцию переменные
. В целевую функцию переменные 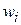
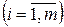 вводят с коэффициентом «M» в случае решения задачи на минимум и с коэффициентом «-М» в случае решения задачи на максимум, где М - большое положительное число. Полученная задача называется М-задачей, соответствующей исходной. Она всегда имеет предпочтительный вид.
вводят с коэффициентом «M» в случае решения задачи на минимум и с коэффициентом «-М» в случае решения задачи на максимум, где М - большое положительное число. Полученная задача называется М-задачей, соответствующей исходной. Она всегда имеет предпочтительный вид.
|
|
|
Пусть исходная ЗЛП имеет каноническую форму записи:
 ;
;
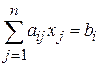 где
где 
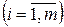 ,
,
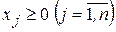 .
.
Если ни одно из ограничений не имеет предпочтительной переменной, то М-задача запишется так:
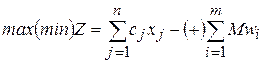 ;
;
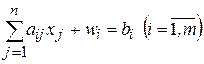 ,
,
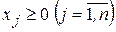 ,
,
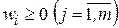 .
.
Тогда начальный опорный план этой задачи: 
Если некоторое уравнение имеет предпочтительный вид, то в него не следует вводить искусственную переменную.
Например, воспользуемся канонической формой записи ЗЛП примера 2 и найдем начальный опорный план методом искусственного базиса.
Составим М-задачу:
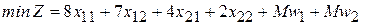 ;
;

Тогда начальный опорный план:  , значение целевой функции на этом плане:
, значение целевой функции на этом плане:
 .
.
Отыскание начального опорного плана
Путем преобразования таблицы Жордана
Для заполнения таблицы Жордана каноническую форму ЗЛП преобразовываем к следующему виду:
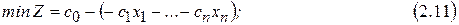
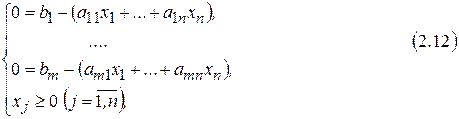
где все 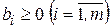 .
.
Таблица Жордана содержит  столбцов, где
столбцов, где 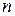 - число переменных,
- число переменных, 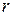 - число переменных в предпочтительном виде и
- число переменных в предпочтительном виде и 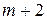 строк, где
строк, где 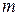 - число ограничений-равенств. В столбце «БП» записываются базисные (предпочтительные) переменные. Если ограничение не имеет предпочтительной переменной, то записывается «0». Столбец «1» - столбец свободных членов
- число ограничений-равенств. В столбце «БП» записываются базисные (предпочтительные) переменные. Если ограничение не имеет предпочтительной переменной, то записывается «0». Столбец «1» - столбец свободных членов 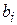
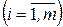 системы ограничений (2.12) а в
системы ограничений (2.12) а в  - строке - элемент
- строке - элемент 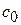 из (2.11). Остальные столбцы «СП», в основной части которых находится элементы
из (2.11). Остальные столбцы «СП», в основной части которых находится элементы  из системы (2.12). В
из системы (2.12). В 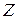 - строке в столбцах «СП» записываются коэффициенты при свободных переменных, стоящие в скобках выражения (2.11). Каждому ограничению - равенству из системы (2.12) соответствует строка основной части таблицы. Целевой функции (2.11) соответствует последняя строка таблицы (таблица 4).
- строке в столбцах «СП» записываются коэффициенты при свободных переменных, стоящие в скобках выражения (2.11). Каждому ограничению - равенству из системы (2.12) соответствует строка основной части таблицы. Целевой функции (2.11) соответствует последняя строка таблицы (таблица 4).
|
|
|
Таблица 4
| СП | ||||||
| БП | 1 | 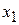
| … | 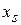
| ... | 
|
| 0 | 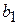
| 
| … | 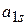
| ... | 
|
| ... | ... | ... | … | ... | .... | ... |
| 0 | 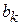
| 
| … | 
| ... | 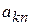
|
| ... | ... | ... | … | ... | ... | ... |
| 0 | 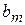
| 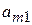
| … | 
| ... | 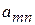
|
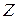
| 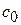
| 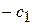
| … | 
| ... | 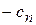
|
Для нахождения начального опорного плана необходимо в результате Жордановых преобразований избавиться от нулей в первом столбце таблицы.
Преобразование таблицы называется шагом Жордановых исключений и осуществляется относительно выбранного разрешающего элемента. Разрешающий элемент выбирается среди положительных чисел основной части таблицы (которая выделена, ) по наименьшему отношению свободных членов (элементы столбца «1» к соответствующим положительным элементам столбца, выбранного разрешающим.
|
|
|
Пусть s-ый столбец будет разрешающим, тогда если  для
для 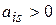 , то
, то  - разрешающий элемент.
- разрешающий элемент.
Шаг Жордановых исключений осуществляется по следующим правилам:
1) Ноль первого столбца в строке разрешающего элемента меняется местами с переменной 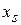 .
.
2) Разрешающий элемент заменяется обратной величиной.
3) Остальные элементы разрешающей строки делятся на разрешающий элемент.
4) Остальные элементы разрешающего столбца делятся на разрешающий элемент и меняют знак на противоположный.
5) Прочие элементы вычисляются по формуле:

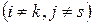 .
.
Или диагональ «прямоугольника», на которой расположен разрешающий элемент  и преобразуемый элемент
и преобразуемый элемент  назовем главной, а другую диагональ - побочной. Тогда преобразованный элемент
назовем главной, а другую диагональ - побочной. Тогда преобразованный элемент 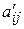 равен разности произведений элементов, расположенных на главной и побочной диагоналях, деленной на разрешающий элемент.
равен разности произведений элементов, расположенных на главной и побочной диагоналях, деленной на разрешающий элемент.
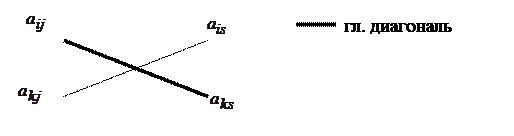
6) 0-столбцы вычеркиваются.
Если система ограничений совместна, то через некоторое число шагов все нули в левом столбце будут замещены переменными  . Тогда начальный опорный план найдём, приравняв свободные переменные к нулю, а базисные (столбец «БП») – к соответствующим свободным членам (столбец «1»).
. Тогда начальный опорный план найдём, приравняв свободные переменные к нулю, а базисные (столбец «БП») – к соответствующим свободным членам (столбец «1»).
|
|
|
Если в ходе Жордановых преобразований встретится 0-строка, в которой все элементы неположительные, то данная система не имеет неотрицательных решений, хотя и является совместной.
Допустим, после некоторого числа шагов Жордановых преобразований все нули в левом столбце замещены переменными  , т.е. получили таблицу 5.
, т.е. получили таблицу 5.
Таблица 5
| СП | ||||||
| БП | 1 | 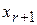
| … | 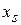
| ... | 
|

| 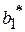
| 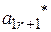
| … | 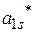
| ... | 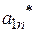
|
| ... | ... | ... | … | ... | ... | ... |
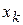
| 
| 
| … | 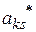
| ... | 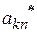
|
| ... | ... | ... | … | ... | ... | ... |
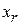
| 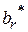
| 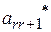
| … | 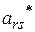
| ... | 
|

| 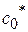
| 
| … | 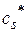
| ... | 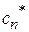
|
Тогда компоненты начальный опорный план 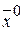 будут:
будут:
БП: 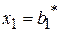 ,…,
,…, 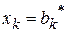 ,…,
,…, 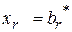 ,
,
СП: 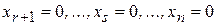 .
.
Таким образом начальный опорный план 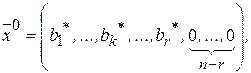 и значение целевой функции на этом плане
и значение целевой функции на этом плане 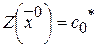 .
.
Например, найдем начальный опорный план ЗЛП примера 2 методом Жордановых исключений. Представим каноническую запись (см. пример 5) в виде (2.11) - (2.12), то есть:
 ;
;

Здесь в третьем и четвёртом ограничениях предпочтительные переменные 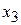 и
и 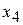 оставлены в левой части.
оставлены в левой части.
Заполним первую Жорданову таблицу (таблица 6).
Таблица 6
| СП | ||||||
| БП | 1 | 
| 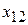
| 
| 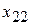
| отношения |
| 0= | 31 | 5 | 0 | 4 | 0 | 31/5 |
| 0= | 36 | 0 | 3 | 0 | 6 | |

| 10 | 1 | 1 | 0 | 0 | 10/1 |
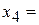
| 10 | 0 | 0 | 1 | 1 | |
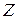
| 0 | -8 | -7 | -4 | -2 |
Начальный опорный план будет найден, если в первом столбце таблицы все нули в ходе преобразований Жордана будут заменены переменными 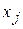 .
.
Пусть 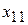 - столбец будет разрешающим. Для нахождения разрешающей строки составим отношения свободных членов к соответствующим положительным элементам этого столбца. Так как в этом столбце только два положительных элемента «5» и «1», то отношения будут
- столбец будет разрешающим. Для нахождения разрешающей строки составим отношения свободных членов к соответствующим положительным элементам этого столбца. Так как в этом столбце только два положительных элемента «5» и «1», то отношения будут 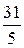 и
и 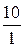 . Так как
. Так как 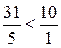 , то элемент «5» и будет разрешающим. Шаг Жордановых исключений относительно найденного разрешающего элемента переводит таблицу 6 в таблицу 7.
, то элемент «5» и будет разрешающим. Шаг Жордановых исключений относительно найденного разрешающего элемента переводит таблицу 6 в таблицу 7.
Таблица 7
| СП | |||||
| БП | 1 | 0 | x12 | x21 | x22 |
| x11= | 31/5 | 1/5 | 0/5 | 4/5 | 0/5 |
| 0= | (36´5-31´0)/5 | 0 | (3´5-0´0)/5 | (0´5-4´0)/5 | (6´5-0´0)/5 |
| x3= | (10´5-31´1)/5 | -1/5 | (1´5-0´1)/5 | (0´5-4´1)/5 | (0´5-0´1)/5 |
| x4= | (10´5-31´0)/5 | 0 | (0´5-0´0)/5 | (1´5-4´0)/5 | (1´5-0´0)/5 |
| Z | (0´5-31´(-8))/5 | 8/5 | (-7´5-0´(-8)/5 | (-4´5-(4´(-8)) /5 | (-2´5-0´(-8))/5 |
Вычеркивая 0 - столбец, получим таблицу 8:
Таблица 8
| СП | ||||
| БП | 1 | x12 | x21 | x22 |
| x11= | 6,2 | 0 | 0,8 | 0 |
| 0= | 36 | 3 | 0 | 6 |
| x3= | 3,8 | 1 | -0,8 | 0 |
| x4= | 10 | 0 | 1 | 1 |
| Z | 49,6 | -7 | 2,4 | -2 |
Пусть теперь разрешающим будет 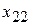 - столбец. Найдем отношения свободных членов к соответствующим положительным элементам этого столбца. Это
- столбец. Найдем отношения свободных членов к соответствующим положительным элементам этого столбца. Это 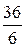 и
и 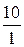 (таблица 9).
(таблица 9).
Таблица 9
| СП | |||||
| БП | 1 | 
| 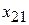
| 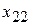
| отношения |
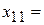
| 6,2 | 0 | 0,8 | 0 | |
| 0= | 36 | 3 | 0 | 6 | 36/6 |

| 3,8 | 1 | -0,8 | 0 | |
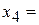
| 10 | 0 | 1 | 1 | 10/1 |

| 49,6 | -7 | 2,4 | -2 |
Так как 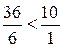 , то вторая строка будет разрешающей. Итак, следующий разрешающий элемент будет «6», и шаг Жордановых исключений переводит таблицу 9 в таблицу 10.
, то вторая строка будет разрешающей. Итак, следующий разрешающий элемент будет «6», и шаг Жордановых исключений переводит таблицу 9 в таблицу 10.
Таблица 10
| СП | ||||
| БП | 1 | x12 | x21 | 0 |
| x11= | 6,2 | 0 | 0,8 | 0 |
| x22= | 6 | 0,5 | 0 | 1/6 |
| x3= | 3,8 | 1 | -0,8 | 0 |
| x4= | 4 | -0,5 | 1 | -1/6 |
| Z | 61,6 | -6 | 2,4 | 2/6 |
Вычеркивая 0 - столбец получим таблицу 11.
Таблица 11
| СП | |||
| БП | 1 | x12 | x21 |
| x11= | 6,2 | 0 | 0,8 |
| x22= | 6 | 0,5 | 0 |
| x3= | 3,8 | 1 | -0,8 |
| x4= | 4 | -0,5 | 1 |
| Z | 61,6 | -6 | 2,4 |
Найдем начальный опорный план, приравняв свободные переменные к нулю, то есть 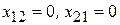 , а базисные переменные к свободным членам, то есть
, а базисные переменные к свободным членам, то есть 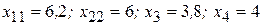 .
.
Значит начальный опорный план:  . На этом плане целевая функция
. На этом плане целевая функция 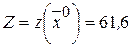 .
.
Итак, благодаря преобразованиям Жордана исходную задачу мы можем записать (исходя из последней таблицы) в виде:
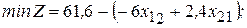
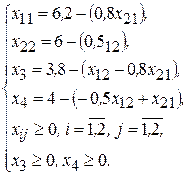
Исследование на оптимальность опорного плана при минимизации целевой функции (второй пункт алгоритма)
Заполним Жорданову таблицу, исходя из задачи, записанной в виде:
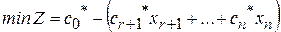 ;
;
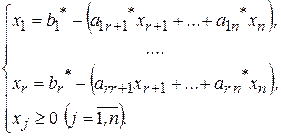
где 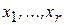 - предпочтительные переменные.
- предпочтительные переменные.
Или воспользуемся конечной таблицей при нахождении начального опорного плана методом Жордановых исключений (таблица 5).
1 Если в Z - строке нет положительных элементов (не считая свободного члена) - план оптимален. Если в Z - строке нет также и нулевых элементов, то оптимальное решение единственное, если же есть хотя бы один нулевой элемент, то оптимальных планов бесконечное множество.
2 Если в Z - строке есть хотя бы один положительный элемент, а в соответствующем ему столбце нет положительных элементов, то целевая функция неограниченна в ОДР (вследствие неограниченности ОДР). В этом случае задача неразрешима. (Проверить правильность составления экономико-математической модели).
3 Если в Z - строке есть хотя бы один положительный элемент и в столбце, содержащем этот элемент, есть хотя бы один положительный элемент, то можно перейти к новому опорному плану, более близкому к оптимальному.
Переход к новому, нехудшему опорному плану (третий пункт алгоритма)
1 В таблице 5 выбираем разрешающий элемент, руководствуясь следующими правилами:
а) выбрать в Z-строке симплекс-таблицы наибольший положительный элемент. Пусть это будет 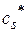 , тогда столбец
, тогда столбец 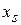 будет разрешающим;
будет разрешающим;
б) найти отношения 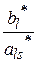 для положительных элементов (
для положительных элементов ( 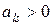 ) столбца
) столбца  ;
;
в) выбрать среди этих отношений наименьшее, скажем 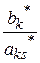 , тогда элемент
, тогда элемент 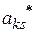 - есть разрешающий (генеральный).
- есть разрешающий (генеральный).
2 Перейти от данной таблицы к следующей таблице по правилам работы с симплекс-таблицей (см. шаг Жордановых исключений).
Замечание: При решении задачи ЛП на максимум целевой функции, ее можно преобразовать в эквивалентную ей задачу на минимум, и решать вышеизложенным методом.
Пример 7
Воспользуемся результатами, полученными в предыдущем примере (см. таблицу 11). Так как в Z – строке есть положительный элемент, то найденный опорный план не оптимален. Поскольку максимальный положительный элемент Z-строки находится в столбце  , то этот столбец будет разрешающим. Составим отношения свободных членов к соответствующим положительным элементам этого столбца (см. таблицу 12). По наименьшему отношению выберем разрешающую строку. Так как
, то этот столбец будет разрешающим. Составим отношения свободных членов к соответствующим положительным элементам этого столбца (см. таблицу 12). По наименьшему отношению выберем разрешающую строку. Так как 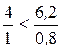 , то
, то 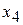 - строка будет разрешающей. На пересечении разрешающего столбца и разрешающей строки найдем разрешающий элемент «1» (См. таблицу 12).
- строка будет разрешающей. На пересечении разрешающего столбца и разрешающей строки найдем разрешающий элемент «1» (См. таблицу 12).
Таблица 12
| СП | ||||
| БП | 1 | x12 | x21 | отношения |
| x11= | 6,2 | 0 | 0,8 | 6,2/0,8 |
| x22= | 6 | 0,5 | 0 | |
| x3= | 3,8 | 1 | -0,8 | |
| x4= | 4 | -0,5 | 1 | 4/1 |
| Z | 61,6 | -6 | 2,4 | |
Шаг Жордановых исключений переводит таблицу 12 в таблицу 13:
Таблица 13
| СП | |||
| БП | 1 | x12 | x4 |
| x11= | 3 | 0,4 | -0,8 |
| x22= | 6 | 0,5 | 0 |
| x3= | 7 | 0,6 | 0,8 |
| x21= | 4 | -0,5 | 1 |
| Z | 52 | -4,8 | -2,4 |
Так как в Z-строке нет положительных элементов, то полученный план оптимален. Найдём его, приравняв свободные переменные к нулю, а базисные переменные – к свободным членам, т. е:
СП:  БП:
БП: 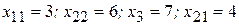 , следовательно
, следовательно 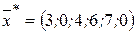 и
и 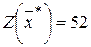 .
.
Так как в Z-строке нет нулевых элементов, то полученный оптимальный план единственен.
Экономический смысл полученного решения задачи примера 2:
для того, чтобы затраты были минимальными необходимо, чтобы оборудование А1 выпускало 3 часа продукцию Р1, оборудование А2 выпускало 4 часа продукцию Р1 и 6 часов продукцию Р2. При этом продукция будет выпущена с минимальными затратами, равными 52 усл. ден. ед. и в заданный срок.
ТРАНСПОРТНАЯ ЗАДАЧА
ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Дата добавления: 2018-09-20; просмотров: 345; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!

