Рекурсивные и нерекурсивные систем
Линейная дискретная система называется рекурсивной, если хотя бы один из коэффициентов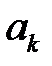 
, 
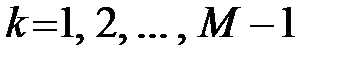, разностного уравнения (6) не равен нулю.Порядок рекурсивной ЛДС равен: 
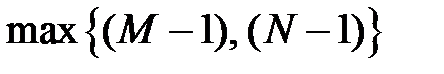Согласно (6) реакция 
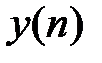рекурсивной ЛДС в каждый момент времени 
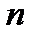определяется:текущим отсчетом воздействия 
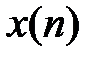;предысторией воздействия 
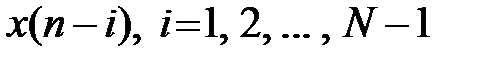;предысторией реакции 
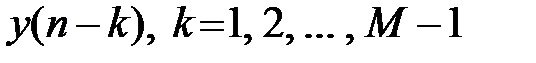.Приведём примеры разностных уравнений простейших рекурсивных ЛДС:первого порядка 
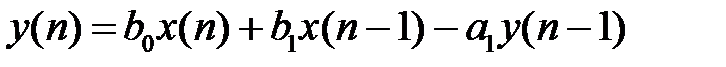(8 ) второго порядка 
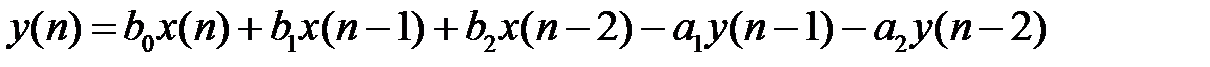Линейная дискретная система называется нерекурсивной, если все коэффициенты 
разностног уравнения (6) равны нулю 
, 
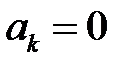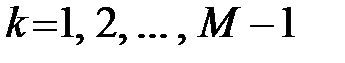. (10)Для нерекурсивной ЛДС разностное уравнение (6) имеет вид: 
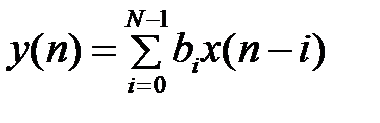, (11)а порядок нерекурсивной ЛДС равен 
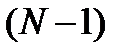.Согласно (11) реакция 
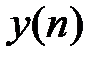нерекурсивной ЛДС в каждый момент времени 
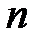определяется:текущим отсчетом воздействия 
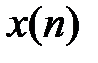предысторией воздействия 
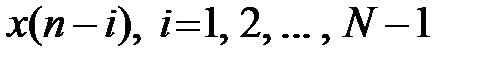.Приведём пример разностного уравнения нерекурсивной ЛДС второго порядка: 
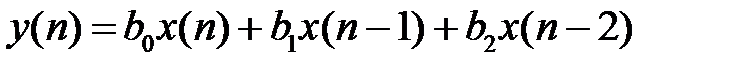. (12)
Определение импульсной характеристики h(nT)
Это реакция линейной дискретной системы на цифровой единичный импульс u0(nT) при нулевых начальных условиях.
2.1. Свойства импульсной характеристики нерекурсивных систем
ИХ нерекурсивной системы 3-го порядка:
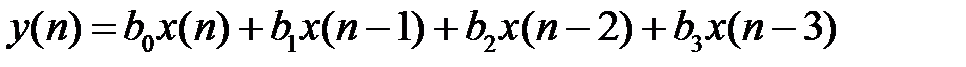
при воздействии цифрового единичного импульса
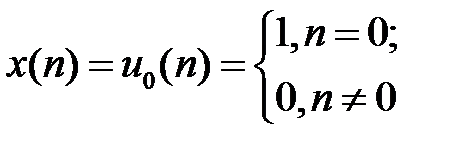
и при нулевых начальных условиях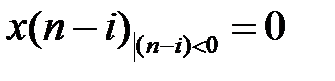 
получаем:
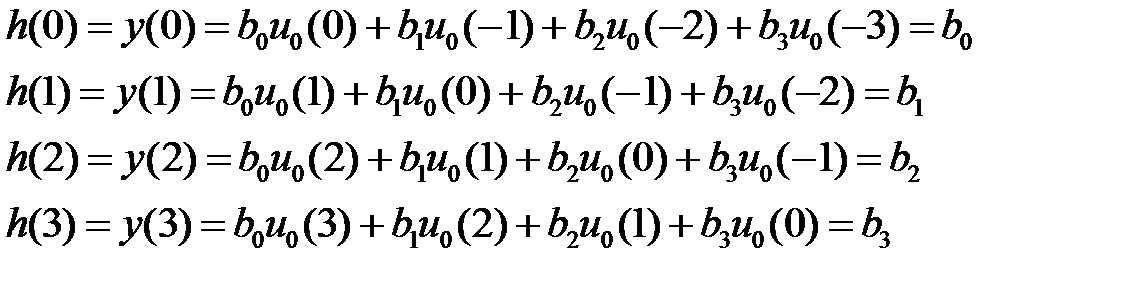
Следствия:
1) длительность ИХ конечна и равна (N – 1)T; число отсчётов импульсной характеристики равно N; такие системы называются КИХ-системами (КИХ-фильтрами);
|
|
|
2) отсчёты ИХ КИХ-системы равны коэффициентам разностного уравнения, т. е. коэффициентам передаточной функции:
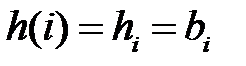
это свойство является основным свойством импульсной характеристики КИХ-систем.
2.2. Свойства импульсной характеристики рекурсивных систем
ИХ рекурсивной системы 1-го порядка
при воздействии цифрового единичного импульс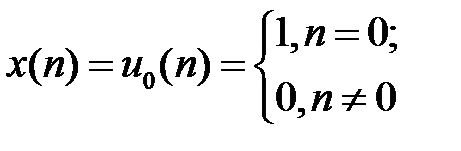 
и при нулевых начальных условиях: 
.
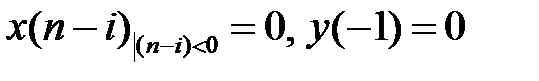Пример 2.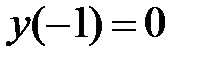 
Решим уравнение методом прямой подстановки:
;
;
;
;
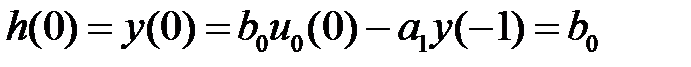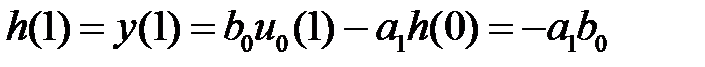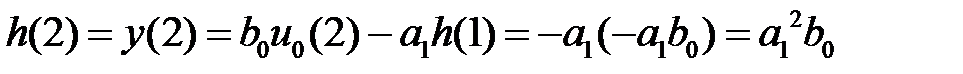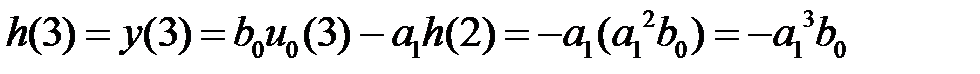Вычисление ИХ можно продолжать бесконечно по формуле:
импульсная характеристика рекурсивной ЛДС имеет бесконечную длительность. Поэтому их называют системами с бесконечной импульсной характеристикой (БИХ-системами).
Устойчивость ЛДС, критерий устойчивости во временной области
ЛДС называется устойчивой, если при ограниченном воздействии
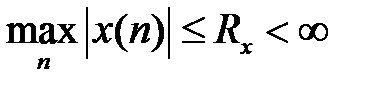
и произвольных, но ограниченных начальных условиях реакция будет также ограниченной: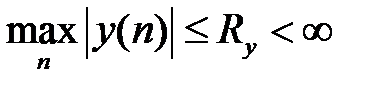 
.
Критерий устойчивости формулируется следующим образом: для того чтобы линейная дискретная система была устойчива, необходимо и достаточно, чтобы выполнялось условие абсолютной сходимости ряда:
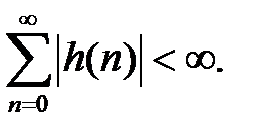
КИХ-системы устойчивы абсолютно в силу конечности их импульсных характеристик.
|
|
|
С БИХ-системами дело обстоит сложнее: пусть импульсная характеристика БИХ-системы имеет вид дискретной экспоненты:
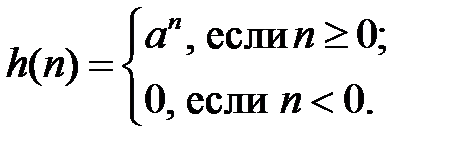
Рассмотрим три варианта: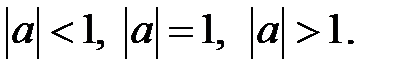 
выводы:
рекурсивные ЛДС (БИХ-системы) требуют проверки на устойчивость;
импульсная характеристика устойчивой рекурсивной ЛДС имеет характер затухающей функции времени.
Определение Z-преобразовани
Z-преобразованием последовательности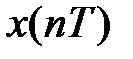 
при условии, что 
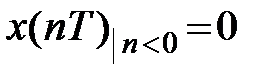, называется ряд 
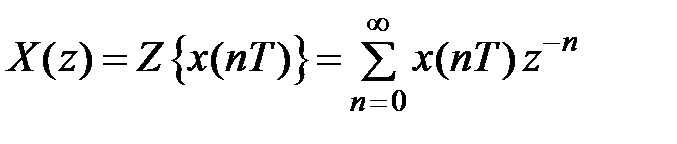, (1)где:
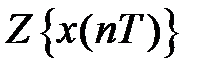— Z-изображение; 
— оригинал.
Z-преобразование получается на основе преобразования Лапласа (1) в результате действий, приводящих к замене переменных: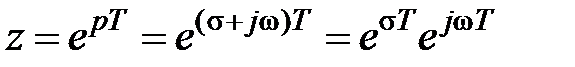 
, (2)где:T – период частоты дискретизации, 
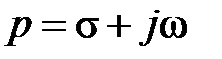– оператор Лапласа.Основные свойства Z-преобразовани
Линейность:Если последовательность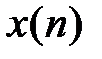 
равна линейной комбинации последовательностей 
,то ее z-изображение равно линейной комбинации z-изображений данных последовательностей:
Z-изображение задержанной последовательности (теорема о задержке).Z-изображение последовательности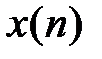 
, задержанной на 
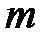отсчетов, равно z-изображению исходной последовательности 
, умноженному на 
: 
; 
.
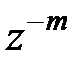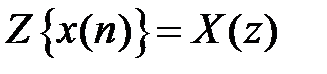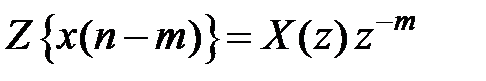Z-преобразование свертки последовательностей (теорема о свертке).Сверткой последовательносте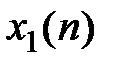й 
и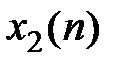 
называется последовательность 
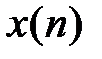, определяемая соотношением 
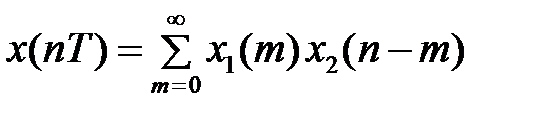.Z-изображение свертки равно произведению z-изображений свертываемых последовательностей 
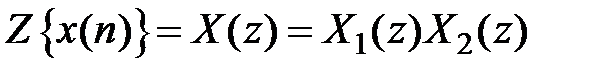.Z-изображения функций типовых дискретных сигналов:Z-изображение цифрового единичного импульса 
: 
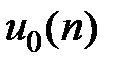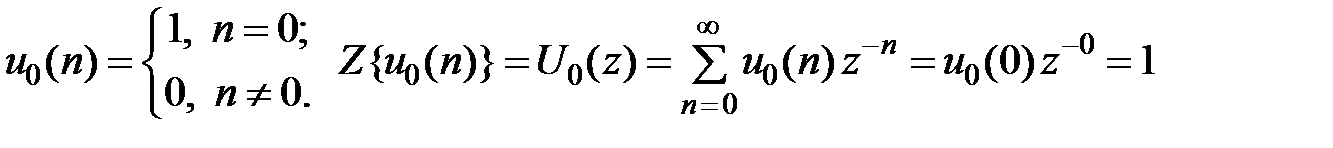Z-изображение задержанного цифрового единичного импульса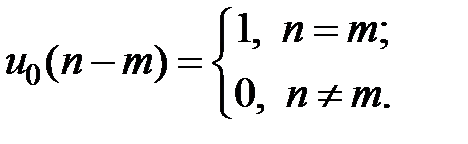 
|
|
|
На основании теоремы о задержке имеем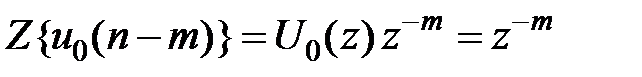 
.
Z-изображение цифрового единичного скачка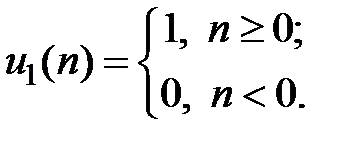 
Z-изображение задержанного цифрового единичного скачка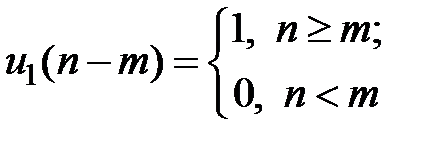 
на основании теоремы о задержке: 
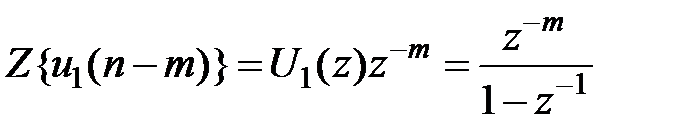.Z-изображение убывающей дискретной экспоненты 
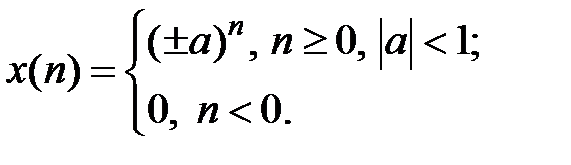Z-изображение взвешенной задержанной убывающей дискретной экспоненты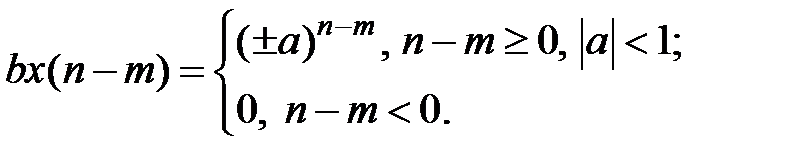 
Z-изображение последовательности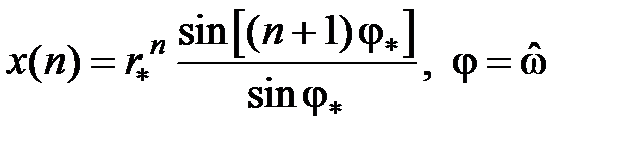 
представляет собой
Дата добавления: 2018-08-06; просмотров: 559; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!