Дискретизация непрерывных сигналов
При передаче непрерывных сообщений по системам связи c использованием импульсной модуляции или кодирования возникает необходимость дискретизации сообщений по времени (см. рис 2).
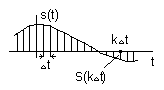
Рисунок 2 -
Сущность дискретизации заключается в том, что непрерывность во времени функции 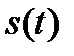 заменяется последовательностью коротких импульсов, амплитуды которых (координаты)
заменяется последовательностью коротких импульсов, амплитуды которых (координаты) 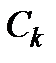 определяются с помощью дискретных весовых функций
определяются с помощью дискретных весовых функций 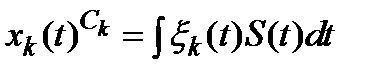 .
.
Воспроизведение непрерывной функции по ее дискретным координатам производится с помощью системы базисных функций
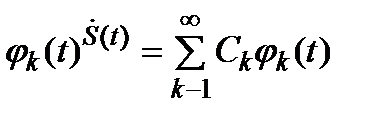 .
.
Иногда весовые и базисные функции принимают одинаковыми 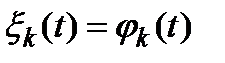 .
.
Более широкое распространение получили методы дискретизации, при которых сигнал  заменяется совокупностью его мгновенных значений
заменяется совокупностью его мгновенных значений  , называемых выборками, или отсчетами. Роль весовых функций в этом случае играют d-функции
, называемых выборками, или отсчетами. Роль весовых функций в этом случае играют d-функции 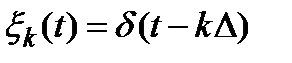 , Dt - шаг дискретизации (может быть неравномерным).
, Dt - шаг дискретизации (может быть неравномерным). 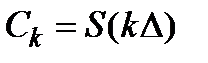 . Шаг дискретизации должен быть таким, чтобы было возможно восстановление непрерывной функции по ее отсчетам с допустимой точностью.
. Шаг дискретизации должен быть таким, чтобы было возможно восстановление непрерывной функции по ее отсчетам с допустимой точностью.
Равномерная дискретизация. Теорема Котельникова
Правило выбора предельного шага при равномерной дискретизации с использованием модели сигнала с ограниченным спектром сформулировано академиком В.А. Котельниковым.
Теорема Котельникова
Любая непрерывная функция 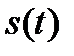 , спектр которой ограничен частотой
, спектр которой ограничен частотой 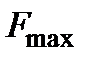 , полностью определяется последовательностью своих значений в моменты времени, отстоящие друг от друга на интервал
, полностью определяется последовательностью своих значений в моменты времени, отстоящие друг от друга на интервал 
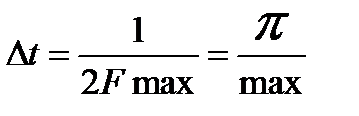 ".
".
|
|
|
Теорема Котельникова дает способ точного восстановления сигнала 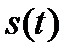 по его отсчетам.
по его отсчетам.
На практике из-за не идеальности элементов схем, используемых для дискретизации, в частности, фильтра нижних частот, берут запас по частоте дискретизации в 1,5÷2,5 раза. 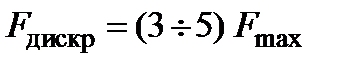
Ряды Фурье
Для представления периодических сигналов 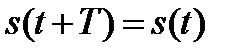 с периодом T базисные функции
с периодом T базисные функции 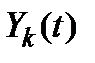 также должны быть периодическими с периодом
также должны быть периодическими с периодом 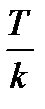 ,
, 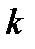 ‑ целое число.
‑ целое число.
В радиотехнике в качестве базисных функций разложения Фурье используют тригонометрические функции. Это объясняется следующими причинами:
а) функции 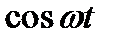 ,
,  являются простыми, определены при всех значениях t, являются ортогональными и составляют полный набор при кратном уменьшении периода;
являются простыми, определены при всех значениях t, являются ортогональными и составляют полный набор при кратном уменьшении периода;
б) гармоническое колебание является единственной функцией времени, сохраняющей свою форму при прохождении колебания через линейную систему с постоянными параметрами, могут изменяться лишь амплитуда и фаза;
в) для гармонических функций и их комплексного анализа имеется мощный математический аппарат, найдены спектры множества форм сигналов;
г) гармоническое колебание легко осуществить на практике.
|
|
|
Кроме гармонического ряда Фурье применяются и другие типы разложения: по функциям Уолша, Бесселя, Хаара, полиномам Чебышева, Ляггера, Лежандра и др.
Гармонический ряд Фурье может быть представлен в следующих видах:

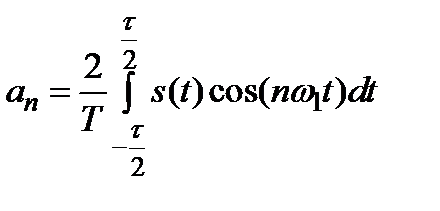 ;
; 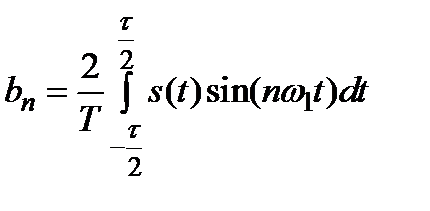 ;
;
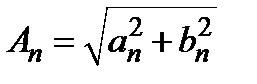 ;
; 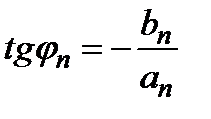 ;
; 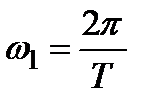 ;
;

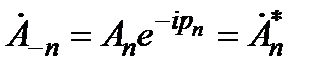
где 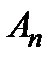 - амплитуда гармоник,
- амплитуда гармоник,
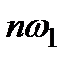 - частота гармоник,
- частота гармоник,
jn - фаза гармоник,
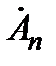 - комплексная амплитуда гармоник.
- комплексная амплитуда гармоник.
Все виды разложения (2.3) тождественны и переходят один в другой.
При выбранном знаке перед jn фаза гармоник является аргументом комплексной амплитуды.
Интегрирование по частям
Из дифференциального исчисления известно, что если u и v - дифференцируемые функции от x, то
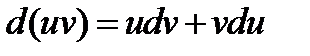 .
.
Отсюда
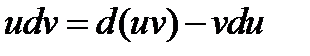 .
.
Интегрируя обе части этого равенства, имеем
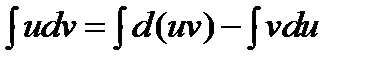
или
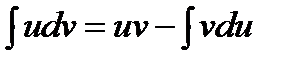 .
.
Интегрированием по частям называется интегрирование с помощью полученной формулы.
Применяется данный способ интегрирования в следующих случаях:
1) подынтегральная функция содержит произведение многочлена от x на показательную функцию от x или произведение многочлена от x на 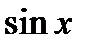 или
или 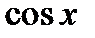 , или произведение многочлена от xна
, или произведение многочлена от xна  ;
;
2) подынтегральная функция представляет собой одну из обратных тригонометрических функций  ,
, 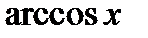 и т.д.;
и т.д.;
3) подинтегральная функция есть произведение показательной функции на  или
или 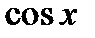 .
.
|
|
|
Пример: необходимо найти интеграл
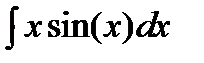 .
.
Положим 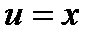 ,
, 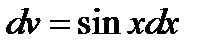 . Тогда
. Тогда 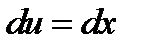 ,
, 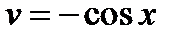 . Отсюда
. Отсюда
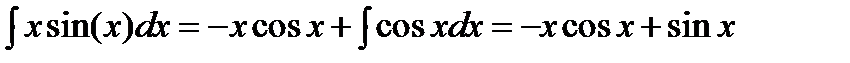 .
.
Дата добавления: 2018-08-06; просмотров: 859; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
