Обоснование структурной схемы ССД.

⇐ ПредыдущаяСтр 5 из 5

Обоснование структурной схемы начинают с анализа технических требований к входным сигналам оконечного устройства АЦП и параметров входных сигналов.

Известно две структуры построения ССД - с аналоговым и цифровым мультиплексированием. Первая структура характеризуется простотой построения, но имеет низкое быстродействие. Вторая - более сложная, но имеет высокое быстродействие.

В соответствии с теорией Котельникова частота квантования сигнала f_к с учетом погрешностей преобразования должна соответствовать

f_к = (3÷5)F_max,

где F_max - максимальная частота спектра сигнала.

Тогда, с учетом количества каналов - n, частота дискретизации составляет

- для ССД с аналоговым мультиплексированием f_KAM = n·f_K

- с цифровым мультиплексированием f_KЦ_M = f_K

Следовательно, выбор первой или второй структуры ССД можно осуществлять на основании сравнения максимального времени преобразования типового АЦП – t_АЦПс необходимой частотой дискретизации.

Если

f_кам ≤ 1/t_ацп,,

то целесообразно использовать схему с аналоговым мультиплексированием.

Если же

f_кам> 1/t_ацпиf_кЦм ≤ 1/t_ацп,

то целесообразно использовать схему с цифровым мультиплексированием.

Если ни одно из условий не выполняется, то необходимо предусмотреть разработку или выбор более быстродействующих АЦП.

После выбора типа структуры ССД необходимо определить наиболее рациональный состав функциональных узлов, которые необходимы для преобразования входного сигнала от датчиков и выдачи их цифрового кода.

Ход рассуждений может быть следующий: АЦП имеет несимметричный аналоговый вход, а датчик симметричный выход. Поэтому в состав аналогового тракта должен входить дифференциальный (разностный) усилитель. Кроме того, в аналоговом канале должна подавляться синфазная помеха, коэффициент ослабления синфазной помехи (КОСС)

КОСС = 2Vс / l_с_min,

где - Vc - напряжение синфазной помехи;

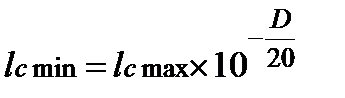- минимальное значение ЭДС сигнала датчика;

D - динамический диапазон изменения входного сигнала, ДБ.

Устройством, ослабляющим синфазную помеху, может стать усилитель с дифференциальным входом.

Схемы выборки — хранения.

Для запоминания изменяющихся аналоговых сигналов на время преобразования, коммутации и других операций в системах сбора информации используют схемы выборки — хранения (рис. .1.88,а), на котором Кл — ключ. Элементом памяти схемы выборки — хранения является конденсатор С, подключаемый на время выборки к источнику сигнала.

Основные параметры этого устройства: время выборки, апертурное время и максимальное время хранения.

Время выборки ограничено снизу постоянной времени цепи заряда τ₃ = R_зС и требуемой точностью запоминания, а сверху — скоростью изменения запоминаемого аналогового сигнала.

Сопротивление цепи заряда R_з= = R_вых + R_o_кл, где R_вых — выходное сопротивление источника сигнала; R_0.кл—сопротивление открытого ключа. На практике время выборки несколько меньше расчетного за счет нелинейного режима источника сигнала в начальный момент заряда.

Когда устройство переходит в режим хранения, некоторая часть заряда утекает с конденсатораСчерез межэлектродную емкость ключа. Связанное с этим зарядом изменение напряжения на конденсаторе называют погрешностью сдвига уровня при переходе в режим хранения. С момента подачи команды «Хранение» до размыкания ключа проходит некоторое время, называемое апертурным. В течение апертурного времени амплитуда запоминаемого напряжения не определена, поэтому в зависимости от требуемой точности запоминания и максимальной частоты переключаемого сигнала на апертурное время накладываются ограничения.

Например, f_max = = 10 Гц, δ = 0,4%, t_а£ 100 мкс.

В режиме хранения максимальная длительность времени хранения сигнала ограничивается сверху разрядом конденсатора С, обусловленным входным током операционного усилителя, дрейфом нуля усилителя, конечным значением входного сопротивления операционного усилителя, токами утечки ключа. Предельное изменение напряжения устройства выборки — хранения

Выражение (1.71) определяет максимальное время хранения при заданной точности операции запоминания.

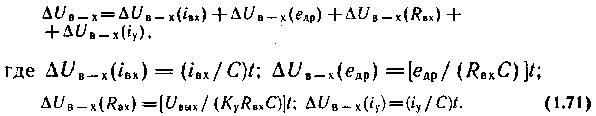
Здесь е_др — напряжение дрейфа.

При необходимости развязки источника сигнала от входа схемы выборки — хранения можно воспользоваться схемой с повышенной точностью, представленной на рис. 1.88,6, которая обладает высоким входным сопротивлением и большим коэффициентом подавления синфазных и сдвиговых погрешностей.

К важнейшим характеристикам устройства выборки — хранения относятся:

время выборки — время от момента подачи сигнала на выборку до момента установления выходного сигнала;

апертурное время — интервал времени между моментом подачи сигнала на хранение и моментом завершения аналого-цифрового преобразования,

скорость разрушения информации — изменение выходного напряжения вследствие разряда запоминающей емкости;

сквозная передача — часть входного сигнала вследствие конечного сопротивления и, разомкнутого ключа передается на выход.

Дискретизация сигналов по уровню и времени, теорема Котельникова. Дискретизация или квантование величин производится любым экспериментатором при считывании результатов измерений со шкалы аналогового измерительного прибора. В цифровых измерительных приборах и в аналого-цифровых преобразователях дискретизация непрерывных величин производится автоматически. Квантование по уровню выполняется при численной регистрации любых экспериментальных данных. С математической точки зрения операция квантования связана с округлениемзначения непрерывной величины в соответствии с принятым правилом (например, отнесение к нижней,верхней границе интервала квантования или к его середине).

Квантованиепо уровню приводит к появлению методической погрешности, которую ввиду ее случайного характера иногда называют шумом квантования. Строго говоря, погрешность дискретизации является неслучайной функцией неизвестного(случайного) значения измеряемой величины.

Наибольшее распространение на практике получило равномерное квантование по уровню, при котором диапазон возможных значений 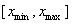непрерывной величины 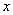разбиваетсяна 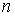равных интервалов квантования

, .

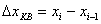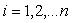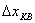называется шагом квантования или шагом дискретизации. При равномерном квантовании .

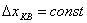В результате дискретизации значение 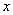попадающее в интервал 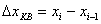округляется до некоторой величины 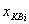которая называется уровнем квантования. В качестве уровней квантования выбирают верхнюю или нижнюю границу интервалов квантования либо их середину (см. рис.4.17). На рисунке уровнем квантования выбраны нижняя граница (а) или – середина (б).

Очевидно, что в случае, изображенном на рис.4.17а,максимальное абсолютное значение погрешности квантования равно шагу квантования, а в случае, изображенном на рис.4.17б - половине шага квантования.Доказано, что при большом 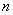(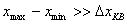) закон распределения погрешностиквантования практически не зависит от закона распределения 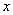и близок к равномерному. Математические ожидания погрешности квантованияврассмотренных случаях различаются (причем на рис.4.17б математическое ожидание равно нулю), а дисперсии погрешности квантования в обоих случаяходинаковы и равны 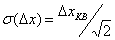. Таким образом, в качестве уровней квантования целесообразно выбрать середины интервалов квантования и соответственно строить технические средства.

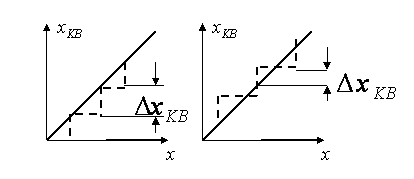
а б

Рис. 4.17

Если закон распределения вероятностей значений измеряемой величины существенно отличается от равномерного, а число уровней квантования в диапазоне измерения невелико (меньше 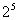), то может оказаться целесообразным неравномерное квантование по уровню, т. е. квантование с переменным шагом. На практике неравномерное квантование по уровню применяется весьма редко, например, в статистических анализаторах.

Дискретизация по времени предполагает представление непрерывной функции 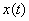в виде дискретного набора значений 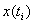и, затем, ее восстановление. Простейший и наиболее распространенный способ временной дискретизации – выбор достаточно малого шага и соединение полученных точек прямыми. При восстановлении непрерывной функции таким образом неизбежно возникают погрешности (см. предыдущий параграф настоящей главы). Для уменьшения этих погрешностей необходимо уменьшить шаг квантования или, возможно, интерполировать функцию 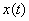на каждом шаге дискретизации степенными многочленами. Современные электронные средства в большинстве случаев позволяют обеспечить достаточно малый шаг дискретизации при оцифровке сигналов, поэтому интерполяция многочленами используется только в особых случаях.

Второй способ дискретизации по времени заключается в том, что непрерывная функция 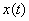заменяется конечным числом коэффициентов разложения 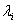, по выбранной системе базисныхфункций .

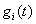В этом случае по каналу связи передаются только коэффициенты разложения, а восстановление исходной непрерывной функции осуществляется путем вычисления суммы 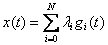. (4.5.5)

Наиболее широкое распространение разложение (4.5.5) получило для функции 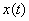и базисных функций 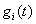, удовлетворяющих теореме Котельникова.

Пусть 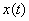имеет ограниченный спектр, то есть ее преобразование Фурье 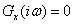при 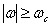, где величина 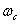называется граничной частотой или частотой среза. Тогда, согласно теореме Котельникова, всегда можно выбрать интервал 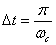такой, что непрерывная функция может быть разложена в ряд

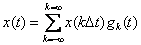, (4.5.6)

где

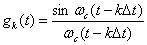. (4.5.7)

Таким образом, теоретически непрерывная функция 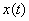может быть точно восстановлена по дискретным отсчетам 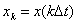, и значениям базисной функции (4.5.7). При этом по каналам связи достаточно передавать дискретные отсчеты .

Разложение функции в ряд Котельникова проиллюстрировано на рис.4.18.

Как уже отмечалось в предыдущем параграфе, в реальных условиях точное восстановление непрерывной функции невозможно из-за того, что не могут быть выполнены условия теоремы Котельникова. Реальные функциивсегда существуют на конечных интервалах времени, поэтому их спектры неограничены. Выбор частоты среза 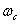и соответствующего шага дискретизации 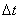приводит к потере высокочастотных составляющих и появлению методической погрешности . За счет конечного времени определения функции (длительности 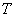), ее спектр ограничен и снизу – частотой .

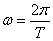Дисперсия относительной погрешности из-за потери высокочастотных составляющих спектра определяется как отношение мощности сигнала в полосе частот 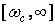к мощности сигнала в полосе 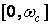, т. е. к мощности той части спектра сигнала, которая может быть принципиально точно восстановлена:

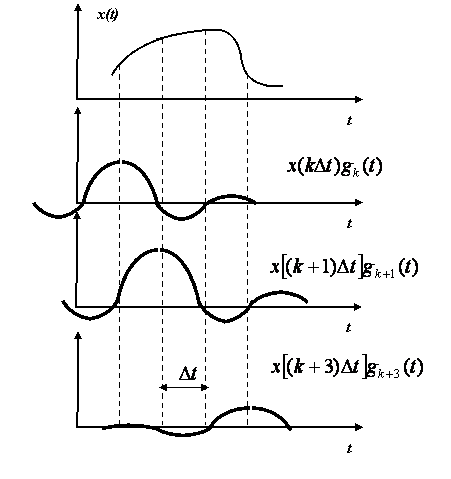
Рис. 4.18

. (4.5.8 )

9.1. Случайные процессы и функции [1, 2, 25].

Случайный процесс описывается статистическими характеристиками, называемыми моментами. Важнейшими характеристиками случайного процесса являются его стационарность, эргодичность и спектр мощности.

Случайный процесс в его математическом описании Х(t) представляет собой функцию, которая отличается тем, что ее значения (действительные или комплексные) в произвольные моменты времени по координате t являются случайными. Строго с теоретических позиций, случайный процесс X(t) следует рассматривать как совокупность временных функций x_k(t), имеющих определенную общую статистическую закономерность. При регистрации случайного процесса на определенном временном интервале осуществляется фиксирование единичной реализации x_k(t) из бесчисленного числа возможных реализаций процесса X(t). Эта единичная реализация называется выборочной функцией случайного процесса X(t). Отдельная выборочная функция не характеризует процесс в целом, но при определенных условиях по ней могут быть выполнены оценки статистических характеристик процесса. Примеры выборочных функций модельного случайного процесса X(t) приведены на рис. 9.1.1. В дальнейшем при рассмотрении различных параметров и характеристик случайных процессов для сопровождающих примеров будем использовать данную модель процесса.

Дата добавления: 2018-08-06; просмотров: 596; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 3 45

Мы поможем в написании ваших работ!