Результат действия оператора Гамильтона на произведения скалярных и векторных полей
Grad, div, rot-три эти дифф.операции могут быть записаны с помощью символического дифференциального оператора, введенного ирл.мат.У.Р.Гамильтонам. Оператор Гамильтона обозначается символом  (набла) и в декартовой системе координат имеет вид:
(набла) и в декартовой системе координат имеет вид:  . Изэти формулы видно, что оператор Гамильтона есть векторный оператор, поэтому иногда называется векторным оператором дифференцирования. Рассмотрим действия оператора Гамеке на произведения скалярных и векторных полей. В этом случае всегда следует иметь в виду, что данный оператор набла представляет собой оператор дифф-я и подчиняется правилу дифф-я произведения. Пусть u,v-некоторые скалярные функции, тогда
. Изэти формулы видно, что оператор Гамильтона есть векторный оператор, поэтому иногда называется векторным оператором дифференцирования. Рассмотрим действия оператора Гамеке на произведения скалярных и векторных полей. В этом случае всегда следует иметь в виду, что данный оператор набла представляет собой оператор дифф-я и подчиняется правилу дифф-я произведения. Пусть u,v-некоторые скалярные функции, тогда  . Аналогично:
. Аналогично:  ,
,  .
.
2. Канонический вид уравнения гиперболического типа. (35 баллов)
Уравнениям гипер-го типа относяться так называемые волновые уравнения:1)Трехмерное волновое уравнения  u=u(x,y,z,t); 2)Одномерное волновое уравнения
u=u(x,y,z,t); 2)Одномерное волновое уравнения  [уравнения колебания струны]; 3)Неоднородное трехмерное волновое уравнения
[уравнения колебания струны]; 3)Неоднородное трехмерное волновое уравнения  [ур.Даламбера]
[ур.Даламбера]
Билет 19)


Билет 20)1. Дифференциальныеоперации второго порядка.


2. Канонический вид уравнения эллиптического типа. (35 баллов)
а) Какие уравнения называют уравнениями эллиптического типа?
б) Приведите примеры уравнений эллиптического типа.

в) Приведите уравнение эллиптического типа к каноническому виду.


Билет 21)
|
|
|
1. Ротор векторного поля. (35 баллов)
а) Что такое ротор векторного поля?
Ротор (Вихрь) — векторный оператор векторного поля, показывает насколько и в какую сторону закручено поле в каждой точке. Ротор обозначается значком rot.
б) По какой формуле можно вычислить ротор векторного поля?

в) Выяснить физический смысл ротора векторного поля.

2.Интегрирование уравнения Лапласа в цилиндрических координатах.
(35 баллов)
а) Запишите уравнение Лапласа в цилиндрических координатах.
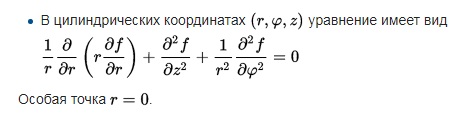
б) Найдите решение уравнения Лапласа в цилиндрических координатах.


Билет 22)
1. Цилиндрическая система координат. (35 баллов)
а) Как определяется положение точки в цилиндрической системе координат?

б) Как связаны цилиндрические и декартовы координаты?
Орты цилиндрической системы координат связаны с декартовыми ортами следующими соотношениями: 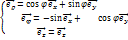 , и образует правую тройку:
, и образует правую тройку: 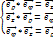 , обратные соотношения имеют вид
, обратные соотношения имеют вид  , закон преобразования координат от цилиндрических к декартовым:
, закон преобразования координат от цилиндрических к декартовым: 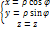 , закон преобразования координат от декартовым к цилиндрических:
, закон преобразования координат от декартовым к цилиндрических:
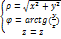 Якобиан равен: J=
Якобиан равен: J= 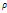
в) Найдите коэффициенты Ламэ в цилиндрической системе координат.

2.Интегрирование уравнения Лапласа в сферических координатах. (35 баллов)
|
|
|
а) Запишите уравнение Лапласа в сферических координатах.
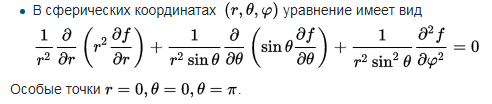
б) Найдите решение уравнения Лапласа в сферических координатах.

Билет 23)
1. Сферическая система координат. (35 баллов)
а) Как определяется положение точки в сферической системе координат?

б) Как связаны сферические и декартовы координаты?

в) Найдите коэффициенты Ламэ в сферической системе координат.

2.Граничные и начальные условия. (35 баллов)
а) Для чего нужны дополнительные условия при рассмотрении задач математической физики?
Для того чтобы найти частное решения к уравнениям описывающие данное физический процесс или явление доюавляются доп.условия.
б) Что такое начальные условия?
Это заданное значения функции и ее производных в начальный момент времени.
в) Назовите виды граничных условий и сформулируйте их.
Дирихле – саодится к заданию функ. На границе области в которой ищется решения задач.
Усл. Неймана- сводится к заданию производных функции на этой границе.
Усл. Каши – сводится к заданию и значения функ. И ее производных на границе где ищется решения задач.
Билет 24)
1. Дивергенция векторного поля. (35 баллов)
а) Дайте инвариантное определение дивергенции векторного поля
|
|
|
Формула Остроградского позволяет дать инвариантное (независимое от системы координат) определение дивергенции векторного поля. С помощью теоремы о среднем для тройных интегралов находим:

где — бесконечно малая поверхность, окружающая данную точку, V — объем области, ограниченной этой поверхностью.
Таким образом, дивергенция векторного поля в какой-нибудь точке равна отнесенному к единице объема потоку векторного поля через бесконечно малую замкнутую поверхность, окружающую данную точку.
б) Назовите основные свойства дивергенции векторного поля.
1) divc= 0 c=const.
2) divλa=λdiva, λ=const.
3) div(ua)=udiva+agradu
4) div(a+b)=diva+-divb
в) Запишите формулу для вычисления дивергенции векторного поля в декартовых координатах.
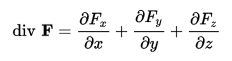
2.Методы решения дифференциальных уравнений в частных производных.
(35 баллов)
а) Назовите методы решения дифференциальных уравнений в частных производных.
Метод Фурье, метод Даламбера, метод функ. Грина, Метод Пуассона
б) В чем заключается метод Фурье?
в) Как с помощью метода Даламбера определяют решение дифференциальных уравнений в частных производных.
г) Изложите суть метода функции Грина.
|
|
|
Он состоит в том что сначала находят некоторое специальные решение задачи того же типа, а затем через него в квадратурах выражают интеграл исходной задачи.
Билет 25)
1. Ротор векторного поля. (35 баллов)
а) Дайте инвариантное определение ротора векторного поля.

б) Назовите основные свойства ротора векторного поля.
1) rot c = 0, c-const.
2) rotλa = λrota, λ=const.
3) rot(a+b)=rota+rotb
4) rot(ωa)= ωrota+|gradω’a|
в) Запишите формулу для вычисления ротора векторного поля в декартовых координатах.
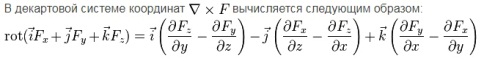
2. Специальные функции. (35 баллов)
а) Назовите цилиндрические функции.
Функции Бесселя
первого рода, ограниченные
второго рода (называемые также «функции Неймана»), неограниченные в нуле
Функции Ганкеля первого и второго рода — комплексные линейные комбинации функций Бесселя и Неймана
Модифицированные функции Бесселя — функции Бесселя от комплексного аргумента, неограниченные монотонные.
первого рода (т. н. «функции Инфельда»[1])
второго рода (т. н. «функции Макдональда»[1])
Функция Бурже — обобщение интегрального представления функции Бесселя
Частные решения неоднородного уравнения Бесселя:
Функция Ангера
Функция Вебера
Функция Струве
Функция Ломмеля
Функции параболического цилиндра
Функции Кельвина
б) Запишите шаровые и сферические функции.

в) Какими свойствами обладает?

{\displaystyle (r,\varphi ,z).}()
{\displaystyle (r,\varphi ,z).}()




 {\displaystyle \ x=0}{\displaystyle {(x,\;y):\;x,\;y\geqslant 0}}
{\displaystyle \ x=0}{\displaystyle {(x,\;y):\;x,\;y\geqslant 0}}
Дата добавления: 2018-08-06; просмотров: 434; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
