Уравнения гиперболического типа и метод их решения
Билет №1
1. В математической физике используют основные формулы векторной алгебры. (35 баллов)
а) Что такое скалярное произведение двух векторов? Приведите основные свойства скалярного произведения двух векторов.
Скалярным произведением двух векторов называется действительное число, равное произведению длин умножаемых векторов на косинус угла между ними.
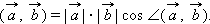
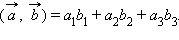
Свойства
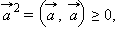
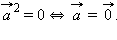
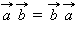 (переместительный закон).
(переместительный закон).
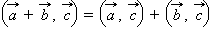 (распределительный закон).
(распределительный закон).
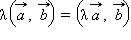 (сочетательный закон).
(сочетательный закон).
б) Чему равен модуль векторного произведения двух векторов? Выразите векторное произведение двух векторов через проекции на координатные оси. Приведите основные свойства векторного произведения.
C=|C|=|ab|=absin(a^b)
Свойства
1)|ab|=-|ba|
2) |λab|=|aλb|=λ|ab|
3) |a(b+c)|=|ab|+|ac|
в) Запишите формулу двойного векторного произведения.
|a|bc||=b(ac)-c(ab)
г) Покажите основное свойство смешанного произведения трех векторов.
(a|bc|)=(b|ca|)=(c|ab|)=-(c|ba|)
2. Рассмотрим задачу об охлаждении бесконечно длинного стержня. (35 баллов)
Билет №2
1. Скалярное поле. (35 баллов)
а) Дайте определение скалярного поля. Приведите примеры скалярного поля.
Если каждой точке Mзаданной области пространства (чаще всего размерности 2 или 3) поставлено в соответствие некоторое (обычно — действительное) число {\displaystyle u} , то говорят, что в этой области задано скалярное поле. Другими словами, скалярное поле — это функция, отображающая R ^nandR (скалярная функция точки пространства).
|
|
|
u скалярное поле обозначается так
u=u(x,y,z) стационарное
u=u(М) точка в пространстве М=(x,y,z)
u=u(x,y,z,t) нестационарное
б) Как графически изображается скалярное поле? Приведите примеры.
Для графического изображения графического скалярного поле используют эквипотенциальные поверхности.
Эквипотенциальыне поверхности совокупность точек которых поле имеет одинаковые значение.
u=u(x,y,z) = const.
Жазык конденсатор сурет
в) Что такое градиент скалярного поля? Покажите основные свойства градиента скалярного поля.
Градие́нт (от лат. gradiens, род.падеж gradientis — шагающий, растущий) — вектор, своим направлением указывающий направление наибольшего возрастания некоторой величины {\displaystyle \varphi } , значение которой меняется от одной точки пространства к другой (скалярного поля), а по величине (модулю) равный скорости роста этой величины в этом направлении.
Свойства:
1) Свойства градиента
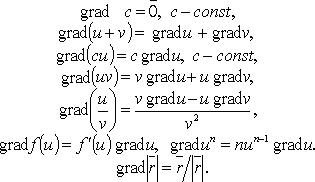
г) По какой формуле вычисляется градиент скалярного поля в декартовых координатах?
Градиент скалярного поля - вектор
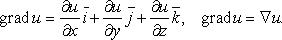
Как вычисляется модуль градиента скалярного поля?
2. Уравнение Лапласа в цилиндрических координатах. (35 баллов)
а) Запишите уравнение Лапласа в цилиндрических координатах.
|
|
|
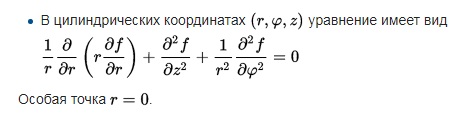
б) Найдите решение этого уравнения методом Фурье


в) Назовите специальные функции, котрые встречаются при решении данного уравнения.
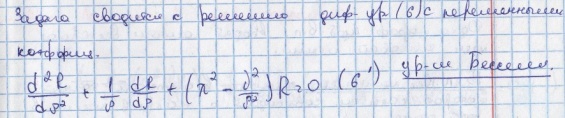
3)
1. Векторное поле. (35 баллов)
а) Дайте определение векторного поля. Приведите примеры векторного поля.
Векторное поле — это отображение, которое каждой точке рассматриваемого пространства ставит в соответствие вектор с началом в этой точке.
б) Как графически изображается векторное поле? Приведите примеры.
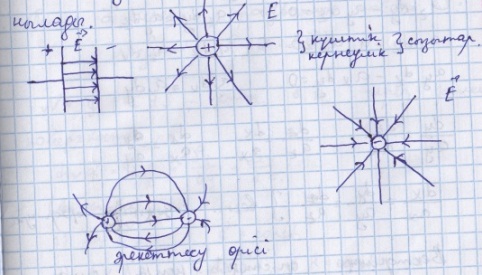
в) Выведите формулу векторных линий.

г) Что такое поток векторного поля через элементарную поверхность, через полную замкнутую поверхность?

2. Уравнение Лапласа в сферических координатах. (35 баллов)
а) Запишите уравнение Лапласа в сферических координатах.
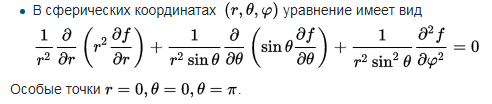
б) Найдите решение этого уравнения методом Фурье.

в) Назовите специальные функции, котрые встречаются при решении данного уравнения.

4)
1. Одной из основных характеристик векторного поля является дивергенция векторного поля. (35 баллов)
а) Что такое дивергенция векторного поля?
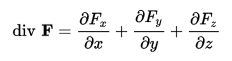 Дивергенцией в.п. в данной точке называется предел к которому стремится отношение потока в.п. через произвольную, окружающую точку, поверхность к ограниченному этой поверхностою обьему ∆V при стремлении последнего к 0.
Дивергенцией в.п. в данной точке называется предел к которому стремится отношение потока в.п. через произвольную, окружающую точку, поверхность к ограниченному этой поверхностою обьему ∆V при стремлении последнего к 0.
|
|
|
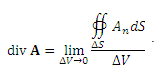
в) По какой формуле вычисляется дивергенция векторного поля в декартовых координатах?
б) Приведите основные свойства дивергенции векторного поля.
Она обладает след.свойствами:
1) divc= 0 c=const.
2) divλa=λdiva, λ=const.
3) div(ua)=udiva+agradu
4) div(a+b)=diva+-divb
г) Сформулируйте теорему Остроградского-Гаусса. Запишите математическое выражение этой теоремы.
Фо́рмула Гаусса — Остроградского — математическая формула, которая выражает поток непрерывно-дифференцируемого векторного поля через замкнутую поверхность интегралом от дивергенции этого поля по объёму, ограниченному этой поверхностью:
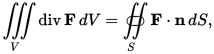
2. Уравнение Бесселя и его решение. (35 баллов)
а) Какой вид имеет уравнение Бесселя?
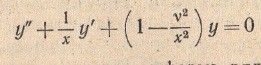
б) Приведите методику решения уравнения Бесселя.


в) Назовите цилиндрические функции. Запишите выражения для цилиндрических функций.

Билет 5)
1. Основные характеристики векторного поля. (35 баллов)
а) Что такое циркуляция векторного поля?
Циркуля́цией ве́кторногопо́ля по данному замкнутому контуру Γ называется криволинейный интеграл второго рода, взятый по Γ. По определению
|
|
|
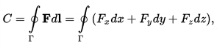
б) Дайте определение ротора векторного поля. По какой формуле вычисляется ротор векторного поля в декартовых координатах?
Ро́тор, ротация или вихрь — векторный дифференциальный оператор над векторным полем.
Ротор (Вихрь) — векторный оператор векторного поля, показывает насколько и в какую сторону закручено поле в каждой точке. Ротор обозначается значком rot или : ▼Х F, где ▼ векторный дифференциальный оператор набла, и F изучаемое векторное поле. В декартовой системе координат ▼Х Fвычисляется следующим образом:
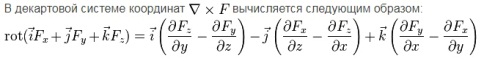
в) Приведите основные свойства ротора векторного поля.
1) rot c = 0, c-const.
2) rotλa = λrota, λ=const.
3) rot(a+b)=rota+rotb
4) rot(ωa)= ωrota+|gradω’a|
г) Сформулируйте теорему Стокса. Запишите математическое выражение этой теоремы.
Теорема Стокса циркулирующая в.п. замкнутая контуру равна потоку ротора этого вектора через произвольную поверхность, опирающийся на данный контур.
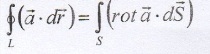
2. Рассмотрим задачу о колебаниях бесконечно длинной струны. (35 баллов)
а) Какое уравнение описывает колебания длинной струны?
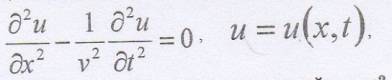
б) Какие дополнительные условия ставятся к задаче?
Были данны только начальные условия
в) Найдите решение этого уравнения методом Даламбера.
Билет 6)
1. Оператор Гамильтона. (35 баллов)
а) Запишите выражение для оператора Гамильтона.
Вспомним определение градиента скалярной функции u = u(x, y, z):
grad u = 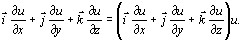
Определим оператор, стоящий в скобках в правой части этого равенства, так:
Определение 16.1. Оператор
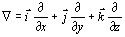
б) Назовите дифференциальные операции первого порядка. Выразите их с помощью оператора Гамильтона.
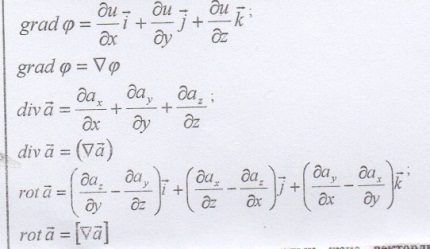
в) Найдите результат действия оператора Гамильтона на произведения скалярных и векторных полей.
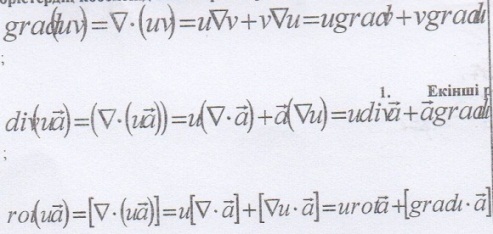
2. Уравнение Лежандра. (35 баллов)
а) Запишите обощенное уравнение Лежандра.
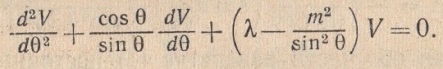
б) Какой вид имеет уравнение Лежандра при 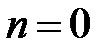 .
.
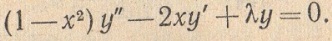
в) Приведите методику решения уравнения Лежандра.


г) Запишите формулы Родриго для полиномов Лежандра.
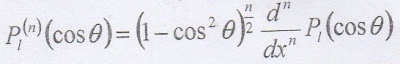
Билет 7)
1. Результат применения оператора Гамильтона к произведению двух векторных полей. (35 баллов)
а) Что такое оператор Гамильтона?
Опера́торна́бла (оператор Гамильтона) — векторный дифференциальный оператор, компоненты которого являются частными производными по координатам. Обозначается символом {\displaystyle \nabla }▼ (набла)
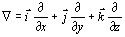
б) Докажите формулу 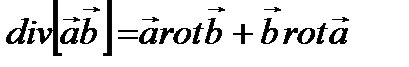
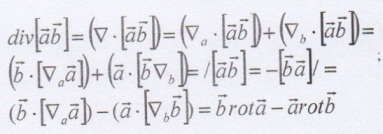
в) Примените векторный оператор дифференцирования к произведению двух векторов и найдите результат 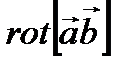 .
.
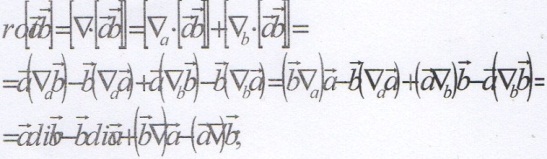
г) Примените векторный оператор дифференцирования к произведению двух векторов и найдите результат 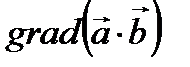 .
.
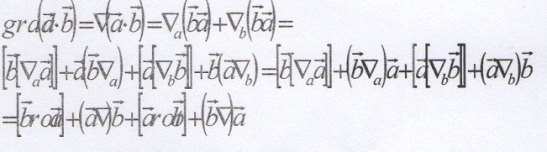
2.Решение дифференциальных уравнений в частных производных методом разделения переменных. (35 баллов)
а) Назовите известные вам методы решения дифференциальных уравнений в частных производных.
Метод Даламбера, Метод Фурье, Метод функции Грина
б) Какова сущность метода разделения переменных?
Метод разделения переменных (метод Фурье) применим не всегда, но в тех случаях, когда им можно воспользоваться, является простейшим. С его помощью можно расщепить уравнение в частных производных для функции n независимых переменных n
Обыкновенных дифференциальных уравнений. Для этого искомую функцию представляют в виде произведения u(x1, x2,….xn)=f1(x1)f2(x2)…fn(xn)
в) Приведите пример использования метода разделения переменных при решении дифференциального уравнения в частных производных.
Билет 8)
1.Дифференциальные операции второго порядка. Оператор Лапласа. (35 баллов)
а) Назовите дифференциальные операции второго порядка.
Оператор Лапласа
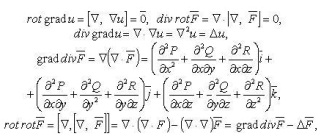
б) Используя оператор Гамильтона, найдите выражения для дифференциальных операций второго порядка.
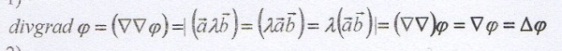
в) Составьте таблицу дифференциальных операций второго порядка.
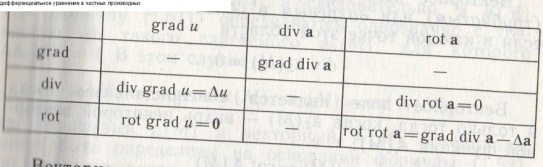
г) Чему равен оператор Лапласа.
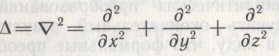
2. Типы дифференциальных уравнений в частных производных. (35 баллов)
а) Что такое дифференциальное уравнение в частных производных?
Дифференциальное уравнение в частных производных— дифференциальное уравнение, содержащее неизвестные функции нескольких переменных и их частные производные.
б) Назовите типы дифференциальных уравнений в частных производных.
Гиперболический, параболический, эллиптический
в) Приведите их примеры.
Билет 9)
1.Классификация векторных полей. (35 баллов)
а) Что такое векторное поле? Назовите виды векторных полей.
Векторное поле — это отображение, которое каждой точке рассматриваемого пространства ставит в соответствие вектор с началом в этой точке. Например, вектор скорости ветра в данный момент времени различен в разных точках и может быть описан векторным полем.
Виды
В.п. дивергенция которого равно нулю наз. Соленоидальное.
В.п. ротор которого равно нулю наз. Потенциальным
В.п. лапласиан которого равно нулю наз. Гармоническим.
б) Какое поле называют соленоидальным? Напишите условие соленоидальности векторного поля.
Векторное поле называется соленоидальным или вихревым, если через любую замкнутую поверхность S его поток равен нулю:
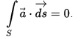
в) Какое поле называют потенциальным? Напишите условие потенциальности векторного поля.
В.п. ротор которого равно нулю наз. Потенциальным
г) Дайте определение гармонического векторного поля. Напишите формулу, выражающую условие гармоничности векторного поля.
Векторное поле A называется гармоническим (или лапласовым), если оно одновременно является безвихревым и соленоидальным:
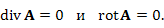
2. Дифференциальные уравнения в частных производных. (35 баллов)
а) Что такое дифференциальное уравнение в частных производных?
Дифференциальное уравнение в частных производных— дифференциальное уравнение, содержащее неизвестные функции нескольких переменных и их частные производные
б) Что называют порядком и интегралом дифференциального уравнения в частных производных?
Порядком дифференциальным уравнения в частных производных называется наивысший порядок производной, входящей в это уравнения.
Процесс нахождения всех решений дифференциального урав. в частных производных называется интегрированием этого уравнения.
в) Дайте определение линейных и нелинейных, однородных и неоднородных дифференциальных уравнений в частных производных.
Дифф. Урав. в частных производных называется линейным, если оно линейно относительно искомой функции и ее частных производных. Все остальные не линейные.
Если функ. Кси – решение урав. и Скси решение этого же урав., то данное урав. называется однородным(С- произвольная постоянная) в противном случае – неоднородным.
г) Напишите формулу, выражающую общий вид линейного дифференциального уравнения в частных производных второго порядка.
Билет 10)
1.Криволинейные ортогональные системы координат. (35 баллов)
а) Дайте определение криволинейных координат. Напишите уравнения, определяющие координатные поверхности. Что такое координатные линии?
Числа q1q2q3 определяющие положение точки в пространстве, назв. Криволинейными координатами.
Пересечение двух координатных поверхностей называется координатной линией.
q 1(xyz), q2(xyz), q3(xyz) координатные поверхности
б) Какую криволинейную систему координат называют ортогональной?
Если ее базисные векторы удовлетворяют следущим соотношениям:
e 1 ∙ e 2= e1∙e3=e2∙e3=0
e1=e2×e3, e2=e3×e1, e3=e1×e2
e1,e2,e3-единичные, e1*e1=e2*e2=e3*e3=1
в) Выразите элементы длин дуг соответствующих координатных линий, элементы площадей координатных поверхностей и элемент объема при помощи коэффициентов Ламе.
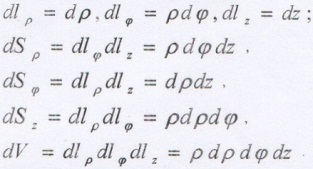
г) Запишите основные дифференциальные операции в криволинейных координатах.
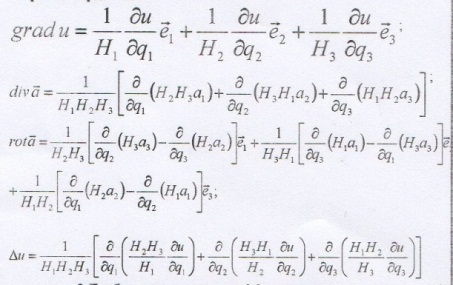
2. Решение дифференциальных уравнений в частных производных методом функции Грина. (35 баллов)
а) Что такое дифференциальное уравнение в частных производных?
Дифференциальное уравнение в частных производных— дифференциальное уравнение, содержащее неизвестные функции нескольких переменных и их частные производные.
б) В чем заключается метод функции Грина?
Фу́нкцияГри́на используется для решения неоднородных дифференциальных уравнений с граничными условиями (неоднородной краевой задачи). Они помогают находить стационарные и нестационарные решения, в том числе при разнообразных граничных условиях.
в) Приведите пример.
Пусть многообразие задаётся первой четвертью плоскости (x,y) :x,y≥0 L- оператор Лапласа. Также предположим, что при х=0 наложены краевые условия Дирихле, при у=0 краевые условия Неймана. Тогда функция Грина примет вид
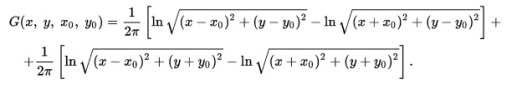
Билет 11)
1.Цилиндрическая система координат. (35 баллов)
а) Назовите цилиндрические координаты. Покажите связь цилиндрических и декартовых координат.
(1)Цилиндрической системой координат называют трёхмерную систему координат, являющуюся расширением полярной системы координат путём добавления третьей координаты(обычно обозначаемой z) которая задаёт высоту точку над плоскостью. Цилиндрические координаты точки состоит изупорядоченной тройкой ( 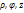 ) а также (x,y,z). Орты цилиндрической системы координат связаны с декартовыми ортами следующими соотношениями:
) а также (x,y,z). Орты цилиндрической системы координат связаны с декартовыми ортами следующими соотношениями: 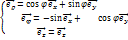 , и образует правую тройку:
, и образует правую тройку: 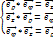 , обратные соотношения имеют вид
, обратные соотношения имеют вид  , закон преобразования координат от цилиндрических к декартовым:
, закон преобразования координат от цилиндрических к декартовым: 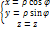 , закон преобразования координат от декартовым к цилиндрических:
, закон преобразования координат от декартовым к цилиндрических:
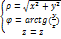 Якобиан равен: J=
Якобиан равен: J= 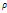
б) Назовите координатные поверхности и координатные линии в цилиндрической системе координат.
Координатными поверхностями в цил.сис.коордатявл.: 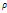 =const-цилиндры с осью 0z;
=const-цилиндры с осью 0z; 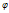 =const-полуплоскости, ограниченные осью 0z;
=const-полуплоскости, ограниченные осью 0z; 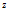 =const-плоскости,
=const-плоскости,  к осью 0z. Коэф-ты Ламев цил.сис.коордат имеют вид:
к осью 0z. Коэф-ты Ламев цил.сис.коордат имеют вид: 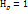 ;
; 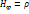 ;
; 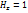 . Их элементы:
. Их элементы: 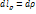 ,
, 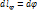 ,
, 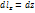 ;
; 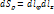 =
= 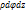 ,
, 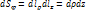 ,
, 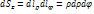 ,
, 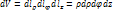 Пересечение двух коорд. поверхностей явл. коорд. линиями.
Пересечение двух коорд. поверхностей явл. коорд. линиями.
в) Определите коэффициенты Ламе в цилиндрической системе координат и выразите элементы длин дуг соответствующих координатных линий, элементы площадей координатных поверхностей и элемент объема при помощи этих коэффициентов Ламе.
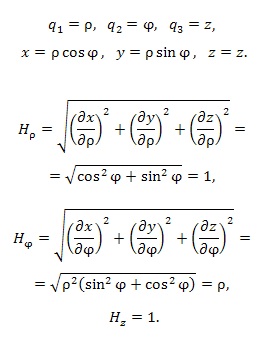
г) Запишите основные дифференциальные операции в цилиндрических координатах.
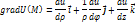
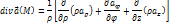
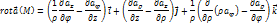
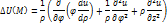
2. Определите потенциал электростатического поля методом функции Грина.
(35 баллов)
а) Запишите уравнение Пуассона для потенциала электростатического поля.
Уравнение Пуассона для потенциала электростатического поля: 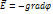 ;
; 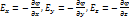 ;
;
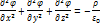
б) Сформулируйте граничное условие для данной задачи.
в) Примените метод функции Грина для определения потенциала электростатического поля.
Билет 12)
1.Сферическая система координат. (35 баллов)
а) Назовите сферические координаты. Покажите связь сферических и декартовых координат.
Сферическими координатами наз. систему координат для отображения геометрических свойств фигуры в трёх измерениях посредством задания трёх координат-( 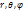 ). Связь между декартовыми и сферическими координатами описывается формулами---
). Связь между декартовыми и сферическими координатами описывается формулами--- 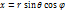 ;
; 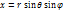 ;
; 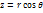 ;
; 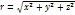 ;
; 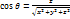 ;
; 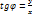 .
.
б) Назовите координатные поверхности и координатные линии в сферической системе координат.
Координатные поверхности в сферической системе координат являются:r=const-сферы с центрами в точке 0; 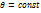 -конусы с осью Oz;
-конусы с осью Oz; 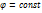 -полуплоскости, ограниченные осью Oz. Координатными линиями будут: (r)=лучи, выходящие из центра 0; линии(
-полуплоскости, ограниченные осью Oz. Координатными линиями будут: (r)=лучи, выходящие из центра 0; линии(  )-окружности с центрами в точке 0 и радиусами r, пересекающие ось Oz;
)-окружности с центрами в точке 0 и радиусами r, пересекающие ось Oz;
в) Определите коэффициенты Ламе в сферической системе координат и выразите элементы длин дуг соответствующих координатных линий, элементы площадей координатных поверхностей и элемент объема при помощи этих коэффициентов Ламе.
Линии (  )-окружности с центрами на оси Oz и радиусами MM3=
)-окружности с центрами на оси Oz и радиусами MM3= 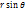 . Коэффициенты Ламе в сферической системе координат
. Коэффициенты Ламе в сферической системе координат 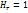 ;
; 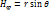 ;
; 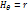 . Элементы:
. Элементы: 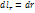 ;
; 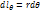 ;
; 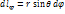 ;
; 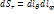 =
= 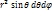 ;
; 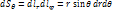 ;
; 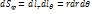 ;
; 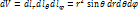 .
.
г) Запишите основные дифференциальные операции в сферических координатах.
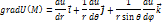
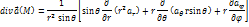
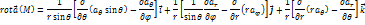
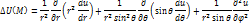
2. Уравнения гиперболического типа и метод их решения. (35 баллов)
Уравнения гиперболического типа и метод их решения
(2)Физические задачи, описываемые уравнениями гиперболического типа
а) Назовите физические задачи, описываемые уравнениями гиперболического типа.
Различные уравнения, получаемые из уравнений Максвелла, описывающие электромагнитное поле.
б) Какие существуют методы решения уравнений гиперболического типа?
Задач Кащи-задача с начальными условиями; Краявая задача-зад. с гранич. Условиями; Смешанная задача-задача который содержит и начальные и граничные условия. Методы решения уравнений гиперболического типа: 1-Метод Фурье; 2-м.Даламбера; 3-м. Функ. Грина.
в) С помощью одного из методов решить уравнение данного типа.
Билет 13)
1.Вектор-функция скалярного аргумента. (35 баллов)
а) Что такое вектор-функция скалярного аргумента?
Если каждому значению переменной t из множества 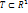 становится в соответствие по определенному закону
становится в соответствие по определенному закону 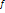 некоторый вектор
некоторый вектор 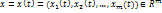 , то говорят что на множестве T задана Вектор функция одной переменной или (вект.функ.скалярного аргумента)
, то говорят что на множестве T задана Вектор функция одной переменной или (вект.функ.скалярного аргумента) 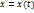 или
или 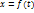 . Вектор-функция
. Вектор-функция 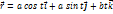 задает в пространстве так называемую винтовую линию. Над вектор-функциями можно производить две основные операции математического анализа – дифференцирование и интегрирование. Они определяются по аналогии с «обычным» анализом. Так, операцию дифференцирования для вектор-функции одного скалярного аргумента можно определить так:
задает в пространстве так называемую винтовую линию. Над вектор-функциями можно производить две основные операции математического анализа – дифференцирование и интегрирование. Они определяются по аналогии с «обычным» анализом. Так, операцию дифференцирования для вектор-функции одного скалярного аргумента можно определить так: 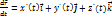 . Можно определить вектор-функцию векторного аргумента как функцию, ставящую в соответствие каждому вектору из некоторого множества векторов Х вектор из множества векторов Y. Правила дифференцирования вектор-функции скалярного аргумента совпадают с правилами дифференцирования для скалярных функции, но учитывают то, что функции векторные. Понятие производной вектор-функции позволяет дать определение неопределенного интеграла. Пусть даны две вектор-функции A(t) и B(t). Тогда B(t) называется неопределенным интегралом (первообразной) A(t), если
. Можно определить вектор-функцию векторного аргумента как функцию, ставящую в соответствие каждому вектору из некоторого множества векторов Х вектор из множества векторов Y. Правила дифференцирования вектор-функции скалярного аргумента совпадают с правилами дифференцирования для скалярных функции, но учитывают то, что функции векторные. Понятие производной вектор-функции позволяет дать определение неопределенного интеграла. Пусть даны две вектор-функции A(t) и B(t). Тогда B(t) называется неопределенным интегралом (первообразной) A(t), если 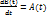 и обозначается как
и обозначается как 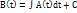 .
.  - постоянный вектор (векторная константа) и это выражение следует понимать как три независимых интеграла от функций
- постоянный вектор (векторная константа) и это выражение следует понимать как три независимых интеграла от функций 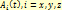 в какой-либо системе координат, в частности, в декартовой. Например, в механике положение точки r(t) определяется, если известна ее скорость, v(t) как,
в какой-либо системе координат, в частности, в декартовой. Например, в механике положение точки r(t) определяется, если известна ее скорость, v(t) как, 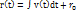 .Аналогично можно ввести понятие определенного интеграла от вектор-функции скалярного аргумента.
.Аналогично можно ввести понятие определенного интеграла от вектор-функции скалярного аргумента.
2. Уравнения параболического типа и метод их решения. (35 баллов)
а) Назовите физические задачи, описываемые уравнениями параболического типа.
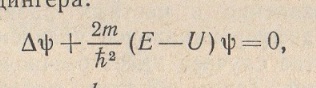 уравнение Шрендингера
уравнение Шрендингера
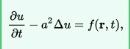 Уравнение теплопроводности
Уравнение теплопроводности
б) Какие существуют методы решения уравнений параболического типа?
(задача Коши для параболического уравнения) используют специальную интегральную формулу, метод разделения переменных Фурье. метод конечных элементов, метод конечных разностей, метод конечных объёмов, а так же их комбинации и другие численные методы,
в) С помощью одного из методов решить уравнение данного типа.

Билет 14)
1.Скалярные, векторные и тензорные величины. (35 баллов)
а) Что такое скалярная величина?
Скалярная величина этовеличина, каждое значение которой может быть выражено одним действительным числом. То есть скалярная величина определяется только значением, в отличие от вектора, который кроме значения имеет направление. К скалярным величинам относятся длина, площадь, время, температура и т. д. б) Что такое векторная величина?
Векторная величина это физическая величина, являющаяся вектором. Противопоставляется с одной стороны скалярнымс другой — тензорным величинам. Также может противопоставляться тем или иным объектам совершенно другой математической природы.
в) Что такое тензор?
Тензор это объект линейной алгебры, линейно преобразующий элементы одного линейного пространства в элементы другого. Частными случаями тензоров являются скаляры, векторы, билинейные формы и т. п. Термин «тензор» также часто служит сокращением для термина «тензорное поле», изучением которых занимается тензорное исчисление.

2. Уравнения эллиптического типа и метод их решения. (35 баллов)
а) Назовите физические задачи, описываемые уравнениями эллиптического типа.
Дата добавления: 2018-08-06; просмотров: 787; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
