Свойства управляющегоконтура, содержащегоLQконтроллер

⇐ ПредыдущаяСтр 4 из 5Следующая ⇒

Прежде чем использовать возможности, которыми управляют контроллеры, основанные на оптимизации квадратичного критериями, нужно знать их свойства. Вопрос устойчивости в контуре управления, использующего данный контролер, очень важен, если поведение становится не устойчивым, то ни одно из других свойств не релевантно. Классический контроллер, типа ПИД часто используется в качестве основы для проектирования. Основным фактором здесь является усиление разомкнутого контура (Циглера-Николса), а при дальнейшем анализе также коэффициент усиления на разных частотах, т. е. частотная характеристика. Тем не менее, различия в поддержании уcтойчивости при использовании контроллера LQ очень разнообразны.

Затем рассматриваются свойства контура управления с использованием контроллера LQ во временной области. Это важно для управления LQ, поскольку его конструкция основана на минимизации критерия, который сам оценивает временное поведение сигналов.

Во временной области будет наблюдаться поведение контура в двух обычных случаях, компенсация помех и изменение заданного значения.

Хотя в линейной системе существует однозначная связь между характеристикой частоты и временной области, существует ряд свойств, которые лучше наблюдаются с точки зрения частоты.Надежность - это один из основных критериев, поскольку подразумевается наблюдение устойчивости и качества поведения управления в тех случаях, когда модель, представленная в конструкции контроллера, отличается от истинной системы.

5.1 Устойчивость

Устойчивость является самым важным требованием контура управления. Преимущество LQ заключается в том, что устойчивость в определенной степени автоматически встроена в конструкцию контроллера. Это утверждение должно включать квалификацию «в определенной степени», поскольку устойчивость может быть теоретически гарантирована только в том случае, если используемая модель является точным соответствием действительности. На практике проблема устойчивости более сложна. Устойчивость должна быть обеспечена тогда, когда реальность зависит от математической модели.

Минимизация квадратичного критерия приводит к решению уравнения Риккати, свойства которого затем могут быть использованы для управления устойчивости. Устойчивость естественным образом гарантируется для бесконечного горизонта T → ∞, где решение задается так называемым алгебраическим уравнением Риккати (ARE)

(2)

Будем рассматривать (2), соответствующую минимизации при T → ∞, где:

● устойчивость;

● не имеет наблюдаемого режима на единичном круге;

●

● является единственным устойчивым решением, а матрица замкнутого цикла имеет собственные значения внутри единичной окружности.

Матричный тип отношения A>Bрассмотрим, как определенность матрицы. Поэтому матрица A больше B (A>B) при условии, что A – B> 0, поэтому A – B является положительно определенной матрицей.

Устойчивость, где горизонт бесконечен, может быть легко решена путем переноса его на бесконечный горизонт, используя следующий шаг. Пусть решение уравнения Риккати, соответствует горизонту критерияT, равно Это относится к решению ARE (2) для других значений

(3)

где 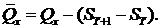Уравнение (3) называется «фальшивым» алгебраическим уравнением Риккати (FARE).

Когда минимизация критерия используется, она решается следующей теоремой.

Если рассматривать уравнение (3), определяющее Если стабилизируется, а обнаруживается, то стабилизируется, а имеет собственные значения внутри единичной окружности.

Из определения сделаем вывод,что последовательность уменьшается, требование устойчивости будет автоматически удовлетворено, так как будет отрицательно полуопределенным. Существует очень сильная связь между монотонностью и устойчивостью в уравнении Риккати. Это можно использовать в качестве основы для формулирования условий, которые гарантируют, что решение уравнения Риккати будет иметь стабилизирующий эффект от заданной итерации k<T, приk= 1.

Теоретическиеправила дают теорему о монотонности решения уравнения Риккати и взаимосвязи между монотонностью и устойчивостью. Следующая теорема оценивает монотонность уравнения Риккати.

Теорема о монотонности: «Если уравнение Риккати имеет неотрицательное решение в итерациях i, i + 1, , 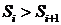и если , то верно , справедливо для всех k> 0».

Если иметь постоянную 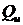, , то потеря будет возрастать от начального значения до значения . Если в момент времени 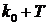значение очень мало и, следовательно, также невелико, между и не будет большой разности .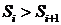

Возьмем итерации из начального условия , что соответствует формулировке критерия, квадратичная форма должна увеличиваться, и поэтому нет ситуации, когда.

Обеспечимустойчивость, то должны найти , , 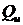такие, что или Это невозможно с базовым критерием, где Предположим, что это приводит к результатам из совокупности суммарной потери, которую представляет S.

Когда устойчивость должна быть обеспечена с использованием квадратичного критерия с конечным горизонтом, то изменяем критерий, чтобы включить его в конечное значение, представленное матрицей . Новый критерий принимает форму

должно быть истинным, если последовательность должна монотонно уменьшаться. Критерий в конечном состоянии должен быть больше, чем совокупная потеря всего процесса компенсации начального состояния. Тогда кумулятивные убытки могут уменьшаться, поскольку потеря каждого отдельного шага в процессе минимизации компенсируется уменьшением конечного состояния и, следовательно, уменьшением его вклада в общую потерю. Рассматривая нулевое ступенчатое управление, потеря будет равна 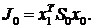В одношаговом управлении общая потеря может быть записана как (конечное состояние ), и это значение может быть меньше , поскольку значение уже меньше из-за управления. Этот процесс может быть продолжен.

может гарантировать, что . Это также относится к простому выбору = αI, где α - вещественное положительное число с высоким значением. Никакое высокое значение α не может обеспечить устойчивость обратной связи с самого начала решения уравнения Риккати. Однако это включает в себя инверсию системной матрицы Это не может быть применено, потому что используемая матрица состояний всегда единственная.

Начальное значение означает дополнительный критерий в конечном состоянии. Если T велико, у него будет только небольшой эффект контроля качества. Однако, если горизонт мал, выбор может существенно изменить управляющее поведение.

Эти замечания приводят к выводу, что относительно трудно гарантировать устойчивость в замкнутом контуре для конечного горизонта T. Однако ситуация не совсем безнадежна.

Устойчивость требований описана выше, но не обязательна.Покажем, что эти условия очень строгие.Устойчивость не обязательно должна быть гарантирована с самой первой итерации. Анализ выбранных примеров поможет в выборе длины горизонта. Рассматривая случаи, когдавозможно использовать ранее полученные знания об устойчивом управлении или априорное знание S, полученное в результате минимизации аналогичного критерия (возможно, для различного значения 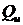илиT и др.). Чтобы обеспечить стабильность контроллера LQ, целесообразно:

●выбирать достаточный длинный горизонт для расчета;

● использовать стратегию IST в адаптивной среде, поскольку это поможет достичь асимптотического бесконечного горизонта.

Рисунки 14,15 показывают положение корней замкнутого контура, который будет получен с помощью контроллера, полученного из i-й итерации уравнения Риккати. Они также иллюстрируют первое и второе различие этого уравнения (точнее, собственные значения матрицы первой и второй разностей уравнения Риккати для отдельных итераций i = 1, 2,3,..., T.

Возможно влиять на количество итераций уравнения Риккати, необходимых для достижения устойчивости, используя 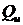и критерий за конечное состояние .

На рисунках 9 и 10приведены графикиустойчивой минимальной фазовой системыS1. Наблюдаем, что устойчивость может быть достигнута независимо от размера значения или начального критерия в состоянии . Также отметим поведение первой и второй разности уравнения Риккати, насколько консервативным является условие достаточности отрицательной определенности для обеих зависимостей. И все же корневой годограф на рисунке 9 показывает, что контроль остается в области устойчивости для всех итераций.

Очевидно, сходимость уравнения Риккати для критерия несколько медленнее, чем для Это связано с тем, что корни замкнутого контура значительно ближе к единичной окружности.

Рисунок 9 – Расположение полюсов с замкнутым контуром.

Система S1: , , горизонт T = [1, ..., 100]

Рисунок 10 - Расположение полюсов с замкнутым контуром.

Система S1: , , горизонт T = [1, ..., 100]

На рисунках 11 и 12показаны графики неустойчивой системыS2. Следует отметить, что начало с имело место в области неустойчивости и, где используется наибольший критерий , требуется большее количество шагов для достижения устойчивого управления. Как и раньше, критерий в конечном состоянии 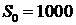ускорил сближение. В дополнение к этому, итерации проходили в устойчивой зоне с самого начала.

Рисунок 11 – Расположение полюсов с замкнутым контуром.

Система S2: , , горизонт T = [1, ..., 100]

Рисунок 12 – Расположение полюсов с замкнутым контуром.

Система S2: , , горизонт T = [1, ..., 100]

5.2 Характеристики LQ управления во временной области

В предыдущем разделе рассматривалась устойчивость как важнейшее свойство управления. Однако больше интересует поведение замкнутого контура. Выход системы зависит не только от входа, но и от возмущающего воздействия. В этом разделе более подробно покажем, как воздействовать на компенсацию возмущения и как адаптивный контроллер реагирует на ситуацию, где действующий тип возмущения не соответствует регрессионной модели возмущения. В дальнейшем рассматривается компенсация для измеряемых возмущений, где возможно использовать управление процессом.

Начнем с компенсации нарушения, в которой существует множество типов помех, и которые воздействуют на выход контролируемого процесса. Это может быть случайный процесс или отклик какого-либо блока на шаг. Если невозможно измерить возмущение, оно должно быть смоделировано. Здесь рассматривается стохастическое возмущение. Характеристика управляющего поведения при компенсации детерминированного возмущения аналогична характеристике управления с заданными точками.

Квадратичный критический синтез контроллера может обеспечить только оптимальную компенсацию возмущения, моделируемую регрессионной моделью. Сначала рассматривается ситуация, когда возмущение характеризуется регрессионной моделью.

В нашей оценке периода выборки используем непрерывную систему с передаточной функцией и случайным возмущением, полученным по мере прохождения белого шума через фильтр с передаточной функцией Если дисперсия шума среднее значение для выхода фильтра также будет равно нулю, то дисперсия будет определяться

Если рассматривать дискретный контроллер с использованием дискретной модели в непрерывном процессе, то один непрерывный процесс времени характеризуется набором дискретных моделей.

В зависимости от выбранного периода выборки, дисперсия возмущений не изменяется при выборке, но генерирует белый шум. Это позволяет получить соотношение для дисперсии исполнительных шумов

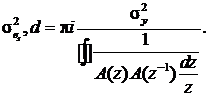
Корневые годографы, показанные на рисунках 9-12, были получены с помощью командной строки, в которую ввели передаточные функции S1 и S2. И получили графики с помощью команды nyquist(w).

Дисперсия генерирующего белого шума будет снижаться, так как увеличивается частота , если случайное нарушение непрерывного времени представлено дискретной моделью для различных периодов выборки.

Поскольку является нижней границей достижимых значений для критериев управления, лучшая компенсация помех может быть достигнута за счет увеличения периода выборки. Эти результаты будут проверены при моделировании в соответствии с моделью, приведенной на рисунке 13.

Рисунок 13 – Схема моделирования компенсации шума

Две системы непрерывного времени, рассматриваемые здесь, моделируются обычным методом с интеграторами и обратной связью. Целью блокаTransferfunction 1является создание помех. Подходящее случайное нарушение получается путем подачи случайного сигнала на вход системы.

ИспользуемблокLimitedwhitenoise, который реализует дискретный белый шум. Достигаем такое поведение, которое имитирует реальность, манипулируя полосой случайного шума, масштабом и длиной графической характеристики. Этот сигнал добавляется к выходу системы, где он одновременно реализует управляемый выход. Функция перевода представляет собой сам управляемый процесс, который, непрерывен во времени - как есть на самом деле.

Поскольку используем контроллер LQ на основе регрессионной модели процесса, фильтр и система установим так, чтобы соответствовало условиям для представления процессав качестве регрессионной модели. Вот почему обе функцииTransfer и Transfer1 имеют один и тот же знаменатель.

Из поведения, показанного на рисунках 14 – 17, видно, что качество компенсации помех зависит от периода выборки. На всех примерах использовался небольшое значениеu, Связь между качеством компенсации и периодом выборки особенно видна при выборе небольшого значения.

Рисунок 14 – Выходнаяфункция (сплошная линия) системы S1

и помехи (пунктирная линия),при

Рисунок 15 – Входная функция системы S1,

при

Рисунок 16 – Выходная функция (сплошная линия) системы S1

и помехи (пунктирная линия),при

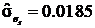
Размер выходного сигнала контроллера не зависит от периода выборки. Более частая выборка дает лучшую компенсацию без увеличения амплитуды входа. Однако, частотный спектр бывает выше.

Рисунок 17 – Входная функция системы S1,

при

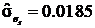
Что касается фиксированного LQконтроллера, то с ним относительно легко справится. Так как он не обеспечит оптимальную компенсацию нарушения. Метод компенсации определяется свойствами замкнутого контура, созданного системой и контроллером. При этом устойчивость не достигается.

Адаптивный LQ контроллер является более сложным. Несоответствие между характеристиками возмущения и величинами, представленными фильтром, вызываетпроцесс идентификации, который определяеткоэффициенты и , так что он прогнозирует возмущение как можно более эффективно(на столько эффективно, на сколько возможно). Это также модифицирует передаточную функцию модели системы. Поведение контроллера на основе таких параметров невозможно определить; его можно оценить только путем анализа надежности контроллера.

Здесь можем продемонстрировать такую ситуацию. Возмущение будет генерироваться фильтром, который имеет передаточную функцию, отличную от

Отслеживание заданных точек является одной из наиболее важных функций контура управления. Качество контроля часто оценивается в виде ответа на типичные изменения заданного значения (step – thestepresponse). Когда проектируется контроллер для отслеживания заданного значения, получим следующие различия с компенсацией помех(возмущений):

●передаточная функция от возмущения до выходных параметров отличаются от передаточной функции,от заданного значения до выхода;

●дальнейший сигнал должен быть учтен в критерии минимизации и необходимо знать его будущие значения.

В отличие от большинства других сигналов в контуре, знание будущего поведения заданного значения на практике очень распространено и естественно. Кроме того, его можно почти всегда применять просто, задерживая истинное изменение заданного значения в течение нескольких (десятков) периодов выборки.

Всегда можно использовать стандартный метод оптимизации, в котором неизвестные значения сигналов в критерии прогнозируются с использованием модели. Такой подход также может применяться к управлению заданными точками. Модель, используемая для прогнозирования будущей постоянной заданной точки

w(k) = w(k – 1).

Рассмотрим ситуацию, когда будущие желаемые выходные значения известны. Если посмотреть на схему контроллера, видно, что оптимизация генерирует как обратную, так и прямую части контроллера. При этом помним, что в адаптивном контроллере компонент прямой связи является интегральной частью функции передачи управления, и любое несоответствие между моделью и реальностью может отразиться на ошибке в отслеживании заданных значений. Переходной функцией фильтра в прямом компоненте является

(4)

при .

Как предполагается, передаточная функция (4) (isnoncausal). Коэффициенты передаточной функции получены с использованием процесса оптимизации. Если управляющий сигнал является постоянным, передаточная функция может быть упрощена

(5)

Выражение получается с использованием процесса оптимизации путем накопления всех будущих заданных точек в один столбец матрицы S. Проще использовать фильтр (5) сразу, если известны другие типы будущего поведения, хотя можно получить конкретные результаты на каждый заданный сигнал. Продемонстрируем это, используя, в качестве примера, рампу. Когда рампа имеет начальное значение и приращение выход фильтра может быть записан как

В процедуре оптимизации это делается, предоставляя матрице Риккати дополнительный столбец, который соответствует приращению на рампе.

На рисунке18 схема планмоделирования для экспериментов по перестановкам заданных значений, включая предварительное программирование. Так как Simulinkне может сгенерировать вектор будущих значений, он должен работать с отложенными реальными значениями и сравнивать выход системы с задержкой заданной точки. Задержка срабатывает в блоке oldval. Произведение 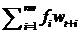выполняется в блокеtrail1. Остальные блоки являются стандартными.

Рисунок 18 – Модель с предварительным программированием

Параметры контроллера с предварительным программированием вычисляются по процедуре lqex3.m, которая состоит из расчета устойчивого оптимального управления, а затем компонента предварительного программирования. Иначе форма предпрограммирующего фильтра была бы обусловлена начальными условиями для уравнения Риккати. Рассмотрим типичное поведение простой системы S1.

На рисунке 19 показан график реакциина скачек выходной функции. А график реакцию входа контроллера можно увидеть на рисунок20.

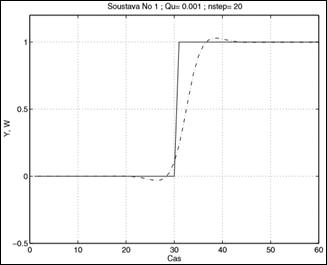
Рисунок 19 – Выходная функция S1, при

Рисунок 20 – Входная функция S1, при

Коэффициенты предпрограммирующего фильтра изображены на рисунке 21, где видим, что приi> 16.

Рисунок 21 – S1: коэффициенты при

Поэтому, если длина предварительного программирования составляет десять (рисунок 22),то значение постоянного состояния будет больше заданного значения, потому что пренебрегаем отрицательными коэффициентами для i> 10.

Рисунок 22 – S1: Выходная функция, при

Аналогично, когда длина предпрограммирования равна пяти (рисунок 23), выход не достигает требуемого значения.

Рисунок 23 – S1: Выходная функция, при

В остальных графиках, изображенных на рисунках24 - 26, виден вход и выход и коэффициенты 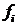для контроллера с использованием различного значения на входе.

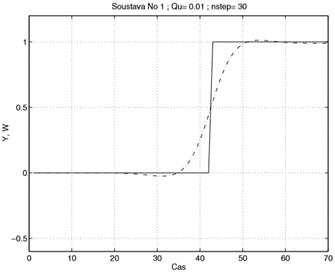
Рисунок 24 – S1: Выходная функция, при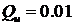

Рисунок 25 – S1: Входная функция, при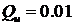

Рисунок 26 – S1: коэффициенты 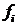при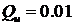

Предварительное программирование использует информацию о будущем контроллере и поэтому обеспечивает оптимальный ответ как с точки зрения качества вывода, так и требований, предъявляемых к вводу.

Типичный недостаток конструкции LQ с использованием критерия минимизации – это ненулевая ошибка установившегося значения в шаговом отклике, когда система не содержит интегратора. Этот offsetособенно очевиден, когда при любой причине должен быть использован более высокий критерий

Стандартным решением этой проблемы является добавление интегратора в openloop. Это также изменяет передаточную функцию фильтра возмущений и, следовательно, также изменяет его предполагаемый характер. Хотя реакция на переход улучшается, компенсация возмущения может ухудшаться. Используя модель ARMAX можнопредположить, чтоС=z – 1, поэтому добавление интегратора не изменяет компенсацию возмущения.

Ошибка установившегося состояния (offset) устраненпутем (penalizing) приращения наu, т.е. (penalizing)Δu. Это не ограничивает размер выходного сигнала контроллера, только изменение в нем.

Также учитывается другой сигнал: опорный вход.В действительности более естественноне (penalize) полный выход контроллер, а только часть остающаяся после вычитания значенияu, необходимого для достижения требуемого уровня выхода. Требуемый размер 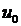можно получить двумя способами:

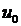● можно принять за другую переменную, которая будет использоваться в критерии минимизации;

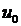● - это сигнал, который пропорционален заданной точке и должен быть добавлен кu(k) для компенсации установившегося состояния.

Второй способ легче интерпретировать и использовать. Модель оffset, показана на рисунке 27. Сигнал 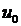будет использоваться для других целей в следующем разделе.

5.3. Характеристики LQ управления в частотной области

Модель регрессии описывает систему с течением времени, в которой критерий минимизации был выполнен во временной области, и продемонстрированы типичные характеристики компенсации возмущений и отслеживания заданных значений.

Рисунок 27 – Модельoffset

Они имеют первостепенное значение для адаптивного контроллера. ДалеерассмотримLQ контроллер по частоте. Особенно важно наблюдать эти свойства, чтобы иметь возможность оценить устойчивость контура и надежность. Которые включают в себя анализ поведения системы и отличаются от модели, используемой в построении управления. Что касается частоты, то также будет проще продемонстрировать эффект периода выборки на усойчивость и качество управляющего поведения. При получении частотной характеристики дискретных систем, полученных при выборке системы непрерывного времени, следует обратить внимание на правильное преобразование частоты. Дискретная передаточная функция представляет только непрерывную частоту более половины частоты дискретизации. Это означает, что период выборки может отражать максимальную угловую частоту

(6)

Эта частота преобразуется путем дискретизации дискретной угловой частоты Поэтому, если иметь дело с контуром управления, в котором дискретная передаточная функция была получена путем выборки, не возможно избежать соотношения между дискретной и непрерывной частотами, возникающими из (6), то

Иногда дискретная частота выражается как отношение к частоте Найквиста, которая равна половине частоты дискретизации В этом случае самая высокая частота имеет значение равное единице. Непрерывная частота получается с использованием и дискретной угловой частоты с использованием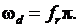

Частотные характеристики контуров контроллера LQ показывают несколько типичных свойств:

● частотная характеристика контроллера LQ имеет тенденцию усиливать сигналы на более высоких частотах;

● частотная характеристика разомкнутого контура в комплексной плоскости (диаграмма Найквиста) отображает типичное поведение вокруг точек (-1, 0) комплексной плоскости;

● контроллер LQ пытается поддерживать частотную характеристику передаточной функции с замкнутым контуром между выходом и заданное значение в логарифмических координатах на самую высокую частоту.

Частотные характеристики в логарифмических координатах полезны для демонстрации эффектов периода выборки. Покажем типичное поведение контроллера на примере управления системой непрерывного времени с передаточной функцией

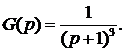(7)

Достигнув совпадения с непрерывной частотной характеристикой до на более высоких частотах значение характеристики периодически повторяется. Из-за используемых логарифмических координат и малости точек на высокой частоте, периодичность и, в частности, симметрия решения искажаются.

На рисунке 28 показана частотная характеристика функции передачи замкнутого контура системы для различных критериев и периода выборки

На рисунке 29 показана функция чувствительности (функция передачи помех) той же системы с периодом выборки

Рисунок 28 – Частотная характеристика замкнутого контура с

различными критериями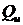

Рисунок 29 – Функция чувствительности для различных критериев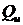

Критерий 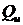сдвигает частотную характеристику контроллера по вертикали и, таким образом, значительно изменяет общий коэффициент усиления разомкнутого контура, изображенного на рисунке 30.

Рисунок 30 – Коэффициент усиления в разомкнутом контуре

для различных критериев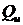

В других типах системы на не минимальной фазе, сдвиг в частотной характеристике контроллера заметно меньше.

Рисунок 31показывает изменение характера функции чувствительности, когда система использует контроллер LQ, полученный оптимизацией одного и того же критерия, но с разными периодами выборки.

Рисунок 31 – Функция чувствительности для

различных периодов выборки

Частотные характеристики передаточной функции с открытым контуром с контроллером LQ показывают типичное поведение, окружая точку (-1,0) в комплексной плоскости.

Форма частотной характеристики может быть выведена из частотной интерпретации уравнения Риккати.

Отправной точкой является стандартная форма алгебраического (стационарного) уравнения Риккати. Частотные интерпретации почти всегда относятся к установившемуся состоянию. Опуская индекс ,используем соотношение для получения

Затем перемещаем выражение в левую часть уравнения и одновременно добавляем и вычитаем на этой стороне выражения и Левой стороной можно манипулировать следующим образом

Затем уравнение умножается слева на а справа на чтобы получить

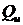Конечный член правой стороны перемещается влево, обе стороны умножаются на слева и G справа, а добавляется к обеим сторонам. Используем соотношение чтобы получить

Для случая с одним входом это можно записать как

Следовательно

(8)

Неравенство (8) интерпретируем: расстояние частотной характеристики от точки (-1,0) в комплексной плоскости всегда больше, чем константа, которая появляется в левой части неравенства.

Взаимозависимость возникает в отношении усложненной манипуляции уравнения Риккати. Аналогичные соотношения динамического контроллера также могут быть получены гораздо более легко из функции передачи системы и полиномиального синтеза контроллера LQ [6]. Продемонстрируем это на упрощенном примере, выполняя в два этапа:

●сначала полином замкнутого контура ϕ вычисляется из уравнения факторизации

(9)

●решение полиномиального уравнения

AR +BS =

в уравнении (9) обозначают сопряженный многочлен для числителя Bи знаменателяA передаточной функции системы, а – коэффициент нормирования, который дает Если разделить (9) на члены и где R - знаменатель передаточной функции контроллера, получим уравнение

(10)

или

(11)

Обратный модуль функции чувствительности находится справа. Из алгоритма решения уравнения Риккати следует, что

Это значение равно элементу минимизированной матрицы Hn. В отличие от пространства состояний (7), где минимальное расстояние частотной характеристики от точки (-1,0) в комплексной плоскости ограничено первым членом в левой части уравнения (8), в уравнении (10) минимальное расстояние также зависит от 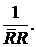Поэтому невозможно требовать гарантированного минимального расстояния.

Надежность — это жизненно важный атрибут всех контроллеров, включая и LQ, для практического применения. Причина проста, это идеальное совпадение между моделью и реальной системой, предполагаемой в построении контроллера, на практике не может быть гарантировано. Есть методы для разработки так называемого надежного контроллера, но обычно это приводит к тому, что контроллер настроен на поддержание определенного качества управления для целого класса систем, которые отличается от модели определенным образом. Качество часто бывает только средним. Здесь преодолеваются проблемы недостаточного знания реальной системы с использованием адаптивного подхода. Несмотря на это, учитываем свойства, определяющие надежность, поскольку адаптация, основанная на идентификации параметров модели, никогда не сможет обеспечить идеальное соответствие. Используются результаты, полученные из нашего анализа частотной характеристики, чтобы наблюдать устойчивость.

При обработке свойств устойчивости в основном рассмотрим устойчивость замкнутого контура системы, для которого контроллер не был изначально разработан.

Размер изменений в системе, которые могут возникать без дестабилизации контура, определяется из кратчайшего расстояния между частотной характеристикой и точкой (-1,0). Это показано на рисунке 32, где

KP = K0+0P

или

Так как конечное выражение является обратным к функции чувствительности, обратное дает модуль функции чувствительности.

В предыдущем разделе показали, как минимальное расстояние между частотной характеристикой с открытым контуром и критической точкой (-1,0) на комплексной плоскости можно найти путем оптимизации.Поэтому результат оптимизации может гарантировать определенный уровень надежности.

Частотная характеристика не пересекается с окружной центрированной точкой (-1,0) сложной плоскости и радиуса максимальное значение модуля частотной характеристики контроллера находится в знаменателе передаточной функции.

Рисунок 32 – Оценка устойчивости от частотной характеристики

В отличие от аналогичных результатов для систем с непрерывным временем, выраженное из уравнения (8), может оказывать положительное воздействие на радиус окружности, так как в зависимости от выбранного периода выборки модуль частотной характеристики может быть достаточно большим в точке ω = π.

Допустимое отклонение стационарного регулятора LQ на изменение коэффициента усиления в диапазоне (1/2 – ∞) и изменение фазы хорошо известно. Это не относится к дискретным системам, в которых структура контроллера выведена из (11). В нашей модели, которая характеризуется выходной обратной связью, характеризуется уравнением (1). Это уравнение дает устойчивость с использованием значения 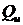как напрямую, так и через знаменатель R. Форма частотной характеристики также зависит от периода выборки. Можем продемонстрировать воздействие этих переменных.

На рисунке33 показана частотная характеристика разомкнутого контура системы полученная в период выборки с контроллером LQ для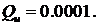

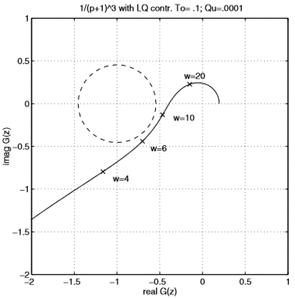
Рисунок 33 – Частотная характеристика с разомкнутым

контуром,

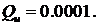
Пунктирная линия обозначает круг, в котором частотная характеристика не может пересекаться. На рисунке 34 показан аналогично, когда период выборки был изменен на 0.5s.

Рисунок 34 – Частотная характеристика с разомкнутым

контуром,

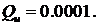
Дата добавления: 2018-08-06; просмотров: 204; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 345 Следующая ⇒

Мы поможем в написании ваших работ!