Линейная фильтрация в дискретном времени

⇐ ПредыдущаяСтр 2 из 3Следующая ⇒

Рассмотрим частный случай линейной фильтрации, когда уравнения наблюдения (12.1) и сообщения (12.2) являются линейными и заданы в виде скалярных разностных уравнений

l(0) = l₀ .

Предполагается, что здесь Н_n = H(t_n) и b_n = b(t_n) есть заданные функции времени; n_n , n_l_n - гауссовские шумы с нулевыми средними значениями и дисперсиями D_n и D_l_n соответственно; интервал времени D = (t_n -t_n_-1) определяется временем дискретизации процессов.

Согласно (12.12) все значения l_n получаются в результате линейного преобразования последовательности независимых распределенных по гауссовскому закону случайных величин n_l_i, i = 0,1,...,n. Поэтому, при гауссовском распределении начального значения l₀ случайная величина l_n будет также распределенной по гауссовскому закону. Совместно гауссовскими будут являться также совокупности случайных величин 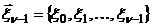и .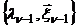

Известно, что условные плотности вероятности совместно гауссовских случайных величин являются гауссовскими. Поэтому плотность вероятности

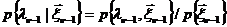
на (n-1)-м шаге является гауссовской и имеет вид

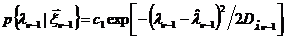где с₁ - нормировочная постоянная, 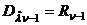- апостериорная дисперсия, 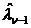- оптимальная оценка .

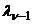Путем соответствующих преобразований можно показать, что условная плотность вероятности на n-м шаге является также гауссовской и имеет вид

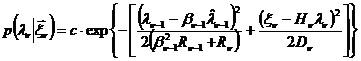. (12.13)

Из формулы (12.13) следуют результирующие уравнения для оценки 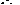и дисперсии 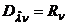, которые определяют дискретный фильтр Калмана. Они носят рекуррентный характер и имеют следующий вид:

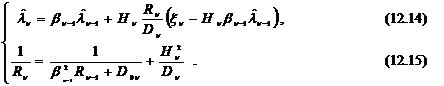
Структурная схема дискретного фильтра Калмана изображена на рис.12.4, где К_n = =Н_n(R_n/D_n).

Предположим, что наблюдения отсутствуют, то есть H(t_n) º 0. Тогда апостериорная плотность вероятности совпадает с априорной и из (12.14) имеем

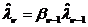Это есть уравнение прогноза 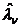по априорным данным. При этом фильтр Калмана вырождается в фильтр, который обведен на рис.12.4 штриховой линией. Это есть формирующий фильтр (ФФ) для передаваемого сообщения l(t). Следовательно, априорные сведения о сообщении "заложены в конструкцию" оптимального фильтра.

На входе дискретного фильтра Калмана из принимаемого колебания x_n вычитается его предсказуемая часть Н_nb_n_-1 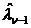. Из этой разности с весовым коэффициентом К_n и из априорных сведений b_n_-1 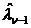формируется оптимальная оценка 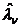. Процедура образования оценки является рекуррентной (то есть повторяющейся), очень удобной для реализации на ЭВМ.

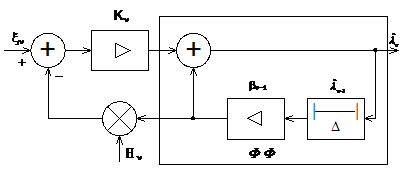
Дискретный фильтр Калмана

В качестве примера рассмотрим фильтрацию неизвестной постоянной величины. Пусть l представляет собой случайную, но постоянную величину; Н_n = 1, n_l_n = 0, b_n_-1 = 1. При этом уравнения (12.11) и (12.12) преобразуются к виду

Примем, что начальное значение l₀ распределено по гауссовскому закону с дисперсией R_v₀, а дисперсия шума n_n постоянна и равна D. С учетом принятых допущений результирующие уравнения для оценки 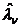(12.14) и дисперсии R_n (12.15) приобретают следующий вид:

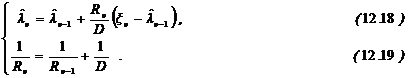
Уравнение (12.18) можно моделировать фильтром, схема которого изображена на рис.12.5. Он состоит из усилителя с коэффициентом усиления R_n /D и рециркулятора (на рисунке он обведен штриховой линией), являющегося дискретным аналогом интегратора.

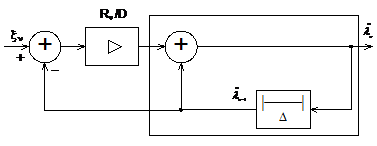
Дискретный фильтр Калмана для постоянной величины

Из уравнения (12.19) для апостериорной дисперсии следует, что 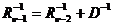. Поэтому 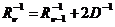. Продолжая расписывать далее, окончательно получим

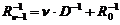. (12.20)

Отсюда следует, что R_n < D/n , то есть, с увеличением числа наблюдений n апостериорная дисперсия убывает, стремясь в пределе к нулю.

Дата добавления: 2018-08-06; просмотров: 308; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 123 Следующая ⇒

Мы поможем в написании ваших работ!