Фильтрация сообщений в канале связи с амплитудной модуляцией
ЛИНЕЙНАЯ ФИЛЬТРАЦИЯ СООБЩЕНИЙ
Оптимальная линейная аналоговая фильтрация. Фильтр Калмана
Наблюдаемый процесс на входе фильтра задан уравнением
x(t) = H(t)l(t) + n(t) , 0 £ t £ T , (12.1)
а сообщение l(t) - уравнением
. (12.2)
Здесь H(t) - известная функция (несущее колебание); H(t)l(t) = s[t, l(t)] - передаваемый сигнал; n(t) - белый гауссовский шум (не обязательно стационарный) с нулевым средним значением и односторонней спектральной плотностью N0; a - постоянный коэффициент, определяющий ширину спектра сообщения l(t). Если сообщение l(t) рассматривают, как результат прохождения формирующего стационарного белого шума nl(t) через интегрирующую цепочку RC, то коэффициент a = 1/(RC).
При линейной фильтрации гауссовских процессов, каким является рассматриваемое сообщение l(t), апостериорная плотность вероятности p[l|x(t)] представляется гауссовским законом. Параметрами такой плотности вероятности служат математическое ожидание 
(t) и дисперсия R(t). Подставляя гауссовскую плотность вероятности в уравнение Стратоновича (11.18), можно прийти к следующей системе уравнений:
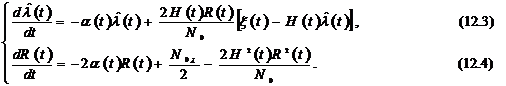
Эти уравнения называют уравнениями фильтра Калмана для непрерывного времени. Первое уравнение определяет алгоритм формирования оценки, а следовательно, и структурную схему фильтра, а второе - ошибку фильтрации (дисперсию оценки сообщения) R(t). Второе уравнение принято в математике называть уравнением Риккати.
|
|
|
Построим структурную схему фильтра Калмана.
Построение схемы удобно начинать с интегратора. Для этого обозначим правую часть (12.3) через y(t) = y1(t)+y2(t), где y1(t) = K(t)H(t)[x(t) - H(t) 
], y2(t) = - a , K(t) = 2R(t)/N0. Коэффициент K(t), зависящий от дисперсии оценки сообщения R(t) и спектральной плотности N0 шумовой помехи n(t), имеет смысл коэффициента передачи. Тогда уравнение (12.3) запишется как d /dt = y(t). Отсюда следует, что если на вход интегратора подать напряжение y(t), то на его выходе получим оценку сообщения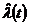 
. Для того чтобы сформировать напряжение у1(t), необходимо иметь генератор несущего колебания H(t), два перемножителя, сумматор и усилитель с коэффициентом усиления K(t).
Фильтр Калмана для гауссовского сообщения при линейной модуляции
С помощью этих устройств осуществляются все операции, входящие в выражение для у1(t). Напряжение y2(t) получается с помощью усилителя с коэффициентом усиления a, на вход которого поступает напряжение оценки 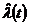. Суммарное напряжение y(t) = y1(t) + y2(t) с выхода сумматора поступает на вход интегратора, на выходе которого получаем оценку .
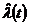Для немодулированного сигнала, когда s(t,l(t)) = l(t), в уравнениях (12.3) и (12.4) нужно положить H(t) = 1. При этом структурная схема фильтра Калмана примет более простой вид (рис. 12.2). В ее состав входят интегрирующий фильтр с постоянной времени RC = 1/[a+2R(t)/N0] и усилитель с коэффициентом усиления K(t).
|
|
|
Фильтр Калмана для гауссовского сообщения при отсутствии модуляции
Рассмотренный фильтр (рис. 12.1) является одним из самых простых. Дальнейшее усложнение фильтра Калмана идет по линии использования формирующего фильтра, который описывается дифференциальным уравнением более высокого порядка, чем уравнение (12.2); гауссовская шумовая помеха n(t) может быть не белым шумом. При этом, как правило, уравнения наблюдения, сообщения и оптимальной фильтрации записываются в матричной форме.
Фильтрация сообщений в канале связи с амплитудной модуляцией
В качестве примера рассмотрим фильтрацию гауссовского марковского сообщения в канале связи с амплитудной модуляцией, когда для передачи сообщения l(t), заданного уравнением, используется следующий сигнал
s(t, l(t)) = l(t) sin w0t. (12.5)
Это сигнал амплитудной модуляции с подавленной несущей. Уравнение наблюдения в этом случае, согласно (12.1)
|
|
|
x(t) = l(t) sin w0t + n(t) . (12.6)
Уравнение оценки согласно (12.3)
или
. (12.7)
Допустим, что период синусоидальных колебаний Т0 = 2p/w0 удовлетворяет, как это обычно бывает на практике, неравенству
T0 <<tk = 1/a, (12.8)
то есть a « w0 , где tk - время корреляции сообщения l(t).
При этих условиях слагаемым cos2w0t можно пренебречь. Тогда уравнение (12.7) преобразуется к виду
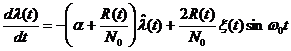. (12.9)
Аналогичным путем можно преобразовать уравнение (12.4) при H(t) = sinw0t:
. (12.10)
Уравнение (12.9) можно моделировать линейным фильтром разомкнутого типа c постоянной времени RC = 1/[a + R(t)/N0].
Структурная схема оптимального демодулятора амплитудно-модулированных сигналов:
Оптимальный фильтр (демодулятор) представляет собой схему когерентного (синхронного) детектора с интегрирующим фильтром RC. В случае обычной амплитудной модуляции с несущей, когда s(t, l(t)) = U0[1+ml(t)] sin w0t , синхронный детектор выделяет огибающую [U0 + mU0 ] и поэтому для получения на выходе оценки сообщения 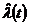в схему (рис.12.3) включены разделительный конденсатор С1, устраняющий постоянную составляющую U0, и аттенюатор А с коэффициентом затухания l/mU0.
|
|
|
Дата добавления: 2018-08-06; просмотров: 350; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!