Критерии оптимальности фильтрации

ФИЛЬТРАЦИЯ ИЗМЕНЯЮЩИХСЯ ПАРАМЕТРОВ СИГНАЛА

Постановка задачи оптимальной фильтрации

В общем случае задача фильтрации формулируется следующим образом. Наблюдается процесс x(t), являющийся детерминированной функцией от полезного сигнала s(t, ) и некоторой помехи n(t).

Полезный сигнал s(t, ) является функцией времени t и многокомпонентного параметра (сообщения) , представляющего собой векторный случайный процесс. Предполагаются известными функциональная зависимость сигнала от аргумента (t) и , а также все необходимые вероятностные характеристики случайного процесса и помехи n(t).

Общая задача фильтрации заключается в том, чтобы на основании априорных сведений и по наблюдаемой реализации x(t) процесса x(t) для каждого момента времени t сформировать апостериорную плотность вероятности сообщения .

В большинстве случаев инженерной практики обычно требуется получить текущую оценку 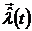, наилучшую в соответствии с выбранным критерием оптимальности. Различают несколько модификаций задачи построения оптимальных оценок. При наблюдении процесса x(t) на текущем интервале времени [0,T] определяется оценка ; если t = 0, имеет место задача текущей фильтрации; если t > 0 - задача фильтрации с предсказанием, или задача экстраполяции; при t < 0 - задача фильтрации с запаздыванием, или задача интерполяции.

Априорные сведения о вероятностных характеристиках сообщения и помехи n(t) задаются либо в форме многомерных плотностей вероятности, либо в виде дифференциальных уравнений с заданными начальными условиями.

Уравнение наблюдения процесса x(t) имеет вид

, (11.1)

где n(t) - гауссовский белый шум с нулевым математическим ожиданием <n(t)> = 0 и d-функцией корреляции < n (t₁) n (t₂) > = (N₀/2) d(t₂ - t₁).

Считаем, что сообщение l(t) однокомпонентный случайный процесс и формируется из белого гауссовского шума n_l (t), имеющего нулевое математическое ожидание и одностороннюю спектральную плотность N₀_l .

Формирование сообщения l(t) определяется дифференциальным уравнением (уравнением сообщения)

, (11.2)

где g (t,l) - известная функция аргументов t и l.

В зависимости от вида уравнений наблюдения и сообщения различают два класса задач фильтрации:

1. Линейная фильтрация – уравнения являются линейными относительно сообщения l(t).

2. Нелинейная фильтрация – уравнения содержит нелинейные функции сообщения l(t).

Очевидно, что линейная фильтрация является частным случаем нелинейной фильтрации. Основополагающие результаты по теории нелинейной фильтрации получены Р.Л. Стратоновичем.

Наблюдение и обработка принятого колебания x(t) могут осуществляться двумя методами: в непрерывном времени (аналоговая фильтрация) и в дискретном времени (дискретная фильтрация). При дискретной обработке берутся временные отсчеты x(t_n) с соблюдением теоремы Котельникова, например, через равноотстоящие промежутки времени t_n₊₁ - t_n = D = = const (рис. 11.1).

В дискретном времени уравнения наблюдения и сообщения имеют следующий вид:

Рис. 11.1

Критерии оптимальности фильтрации

Пусть на входе фильтра наблюдается реализация процесса

(11.5)

где l(t), n(t) - являются реализациями соответственно сообщения и шума.

Рис. 11.2

Фильтр будет оптимальным, если на его выходе формируется процесс y(t), являющийся оптимальной, т.е. наилучшей в определенном смысле, оценкой сообщения .

То, что вкладывается в понятие оптимальной оценки , определяется выбранным критерием оптимальности. Критерий оптимальности сформулируем, исходя из апостериорной плотности вероятности p(l,t|x(t)), определяемой на интервале наблюдения [0,t]. Интервал наблюдения за счет роста t непрерывно увеличивается. Это приводит к увеличению объема выборки и к сужению апостериорной плотности вероятности p(l,t|x(t)), характеризующей плотность вероятности сообщения l(t) в конечной точке интервала наблюдения. Сужение p(l,t|x(t)) соответствует уменьшению дисперсии оценки сообщения R(t) = , что является самым важным результатом фильтрации. На рис. 11.3 показано изменение апостериорной плотности вероятности p(l,t|x(t)) во времени.

При гауссовском белом шуме n(t) и достаточно высоком отношении сигнал/шум , где E_s -энергия сигнала, апостериорная плотность вероятности p(l,t|x(t)), приближается к гауссовскому закону, для которого мода, медиана и математическое ожидание совпадают.

Рис. 11.3

Если в качестве критерия оптимальности рассматривать получение оценки по максимуму апостериорной плотности вероятности

p(l,t|x(t)) = max , (11.6)

то найденная таким образом оценка является оптимальной также по минимуму среднего значения квадрата ошибки между оценкой и передаваемым сообщением:

. (11.7)

Таким образом, если в качестве оценки выбрать траекторию координаты максимума плотности вероятности p(l,t|x(t)), то оценка будет наилучшим образом совпадать с передаваемым сообщением l(t), т.е. критерии оптимальности (11.6) и (11.7) приводят к одной и той же оценке.

Оптимальной оценкой является апостериорное математическое ожидание

. (11.8)

Погрешность получаемой оценки можно характеризовать апостериорной дисперсией

. (11.9)

Дата добавления: 2018-08-06; просмотров: 657; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 Следующая ⇒

Мы поможем в написании ваших работ!