Геометрична інтерпретація множин.

Множини. Способи задання множин.

Множина́ — одне з основних понять сучасної математики. Строго воно не визначається, але може бути дано інтуїтивне визначення множини як сукупності певних і різних об'єктів довільної природи, яка розглядається як одне ціле. Об'єкти, які складають множину, називаються її елементами. Наприклад, можна говорити про множину усіх книг в певній бібліотеці, множину літер українського алфавіту або про множину всіх коренів певного рівняння тощо.

Множина вважається означеною, якщо про кожен об'єкт, що розглядається, можна казати, що він або належить, або не належить множині. Ідентичні (тобто однакові) об'єкти в множині не допускаються.

На письмі множини позначаються, як правило, великими літерами. Для деяких множин у математиці вживаються сталі позначення. Наприклад:

ℕ - множина натуральних чисел,
ℤ - множина цілих чисел,
ℚ - множина раціональних чисел,
ℝ - множина дійсних чисел,
ℂ - множина комплексних чисел.

Способи задання множин

Задання множини за допомогою переліку її елементів.

Нехай множина X складається з елементів a, b, c, ..., k. Для означення цього факту використовується позначення:

X = {a, b, c, ... , k}

A = {4, 2, 1, 3}

B = {червоний, білий, блактиний}

Наприклад, множина натуральних чисел ℕ визначається як:

ℕ = {1, 2, 3, ... , n, ...}

Задання множини вказівкою властивості її елементів.

В математичних задачах, як правило, розглядають елементи деякої цілком означеної множини A. При цьому необхідні елементи виділяють за деякою їх властивістю (або вказують породжуючу процедуру) P, такою що кожний елемент x ∈ A або має властивість P (записується P(x)), або не має її. За допомогою властивості P виділимо множину всіх тих елементів, які мають властивість P. Цю множину будемо позначати як {x ∈ A | P(x)} = {x | P(x)}.

Задання множини вказівкою її властивості (або породжуючим предикатом) слід здійснювати обережно. Наприклад, множина Y = {X|X∉X} (множина всіх множин, які не містять себе в якості елемента) веде до парадокса Рассела і є некоректною в аксіоматичній теорії множин.

Основні поняття теорії множин.

В основі теорії множин лежать первинні поняття: множина та елемент множини. Елемент множини перебуває щодо множини у відношенні бути елементом множини (позначається як 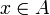^[4] — «x є елемент множини A»). Серед похідних понять найважливішими є наступні:

порожня множина — множина, яка не містить елементів, позначається зазвичай ;
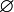підмножина і надмножина — множина, яка складається тільки з елементів іншої множини, та множина, до якої належать усі елементи іншої множини, відповідно;
сімейство множин;
простір (універсум) — множина, що є надмножиною всіх множин;
конституента.

Над множинами визначені наступні операції:

об'єднання (або сума) (позначається як );
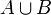перетин (або добуток) (позначається як );
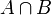різниця (позначається як 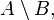рідше );
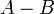симетрична різниця (позначається як 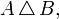рідше ).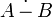
доповнення (позначається як 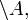або );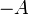

Для множин визначені наступні бінарні відношення:

відношення рівності (позначається як );
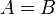відношення включення (позначається як 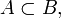або ).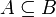

Геометрична інтерпретація множин.

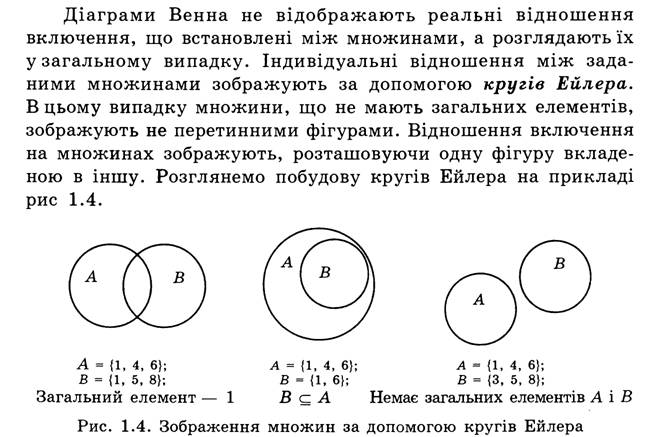
Операції на множинах.

Алгебра множин.

Нескінченні множини.

Нескінченна множина — множина, що не є скінченною. Можна дати ще декілька еквівалентних означень нескінченної множини:

Множина, в якій для будь-якого натурального числа 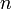знайдеться скінченна підмножина із 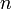елементів.
Множина, в якій знайдеться зліченна підмножина.
Множина, в якій знайдеться підмножина, рівнопотужна деякому (ненульовому) граничному ординалу.
Множина, для якої існує бієкція з деякою його власною підмножиною.

Для будь-якої нескінченної множини існує множина з ще більшою потужністю — таким чином, не існує нескінченної множини найбільшої потужності. Потужності нескінченних множин називаються алефами (англ.) і позначаються 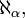де індекс 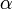пробігає всі порядкові числа. Потужності нескінченних множин складають цілком упорядкований клас — найменшою потужністю нескінченної множини є 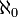(алеф-0, потужність множини натуральних чисел), за ним слідують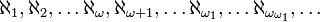

Приклади

Множини натуральних чисел 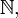цілих чисел 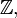раціональних чисел 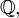дійсних чисел 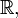комплексних чисел 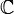— є нескінченними множинами.
Множина функцій 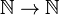є нескінченною.
Упорядкована нескінченна множина може мати «кінці» (мінімальний і максимальний елементи) — наприклад, множина раціональних чисел на відрізку
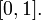
Сукупність усіх нескінченних підмножин зліченної множини є незліченною нескінченною множиною.

Дата добавления: 2018-08-06; просмотров: 788; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 4 Следующая ⇒

Мы поможем в написании ваших работ!