Несмещённая оценка дисперсии возмущений модели парной регрессии.
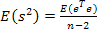
Математическое ожидание суммы квадратов остатков:
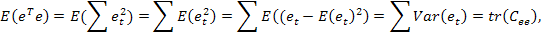
где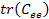 
- след автоковариационной матрицы, который равен сумме её диагональных элементов.
= 
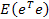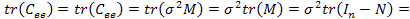
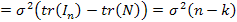
Так как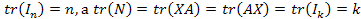 
.
Таким образом, несмещённая оценка дисперсии возмущений:
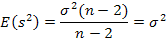
Обозначения:
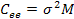– автоковариационная матрица вектора остатков
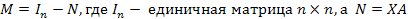, где 
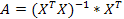
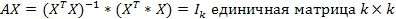
13. Доверительные интервалы параметров парной регрессионной модели.
Рассмотрим доверительный интервал параметра b:
Дробь Стьюдента –нормированная ошибка оценки:
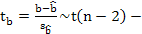распределение Стьюдента, где ( 
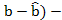ошибка оценки и
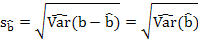
(n-2) – число степеней свободы является параметром распределения Стьюдента.
Доверительная вероятность:
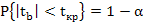, где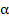 
- уровень значимости
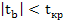или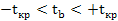 
;
;
.
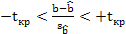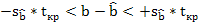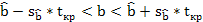Таким образом, границы доверительного интервала параметра b равны:
.
Аналогично определяются границы доверительного интервала параметра а:
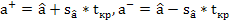
14. Алгоритм построения интервальных оценок параметров регрессионной модели в Excel.
Алгоритм построения доверительных интервалов параметров модели имеет следующую последовательность:
1) оценка параметров модели по выборочным данным производится с помощью функции ЛИНЕЙН при параметрах :Константа =1 (=0, если нет свободного члена), статистика =1(всегда). Эти вычисления будут равноценным вычислениям по формулам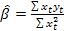 
; 
.
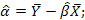
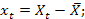
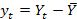2) оценка значений эндогенной переменной и вычисление остатков регрессии: основываясь на данных, полученных с помощью функции линейн подставляем и рассчитываем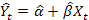 
; 
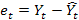, t=1,…,n;
|
|
|
3) оценка дисперсии возмущений, так же получается при применении функции ЛИНЕЙН (в таблице EXCEL находится под данными ско оценки первого регрессора (константы при единичном регрессоре)):данные равносильны вычисляемым по формуле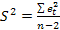 
;
4) оценка дисперсии коэффициентов, так же выводится в функции ЛИНЕЙН под оценками параметров модели. Равносильно квадратному корню из: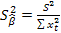 
; 
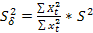
5) выбор критического (табличного значения) статистики tkp(n - 2) Критическое значение t^ статистики Стьюдента можно определить в Excel, в категории «Статистические», при помощи функции «Стьюдраспобр». Параметры функции: вероятность (уровень значимости), число степеней свободы (для парной регрессии n - 2).;
6) вычисление границ доверительных интервалов параметров модели по формулам
; 
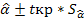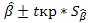
15. Проверка значимости оценок параметров линейной регрессионной модели.
При проверке качества спецификации парной регрессии наиболее важной является задача установления наличия линейной зависимости между эндогенной переменной и регрессором модели. С этой целью проверяется значимость оценки параметров α и β. В процедуре проверки значимости оценки параметра парной регрессии используется дробь Стьюдента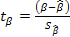 
которая при истинности гипотезы H0:β = 0, против конкурирующей H1: β 
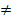0, принимает вид: 
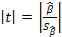,и, при выполнении условий Гаусса—Маркова (относительно случайных возмущений), имеет t-распределение с числом степеней свободы n-2. Аналогично формируется t-статистика для проверки гипотезы H0 значимости параметра α, однако параметр β в парной регрессии имеет более важную роль, так как его значимость соответствует значимости регрессора и наличию линейной связи между переменными модели.
|
|
|
Алгоритм проверки значимости параметра β выполняется в следующей последовательности:
1) оценка параметров парной регрессии;
2) оценка дисперсии возмущений S2;
3) оценка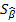 
ско оценки параметра β;
4) выбор значения tкр (по заданному уровню значимости α и числу степеней свободы (n - 2) из таблиц распределения Стьюдента);
5) проверка неравенства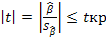 
, при H0: β=0
Если данное неравенство выполняется, то регрессор признается незначимым, если не выполняется, то гипотеза H0: β=0 отвергается и регрессор признается значимым, т. е. между эндогенной переменной и регрессором присутствует линейная зависимость.
При проверке статистической значимости параметров модели можно использовать следующее приближенное правило
|
|
|
1) 
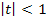, то коэффициент не может быть признан значимым (доверительная вероятность меньше 0,7);
2) 
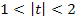, то коэффициент может быть признан значимым с доверительной вероятностью в диапазоне между 0,7-0,95;
3) 
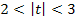, то коэффициент признается значимым с доверительной вероятностью в диапазоне между 0,95-0,99;
4) 
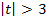, то значимость коэффициента очевидна (доверительная вероятность находится в диапазоне между 0,99 и выше).
Чем больше объем выборки, тем надежнее выводы о значимости коэффициента. При n > 10 приближенное правило дает результаты, близкие к табличным.
16. Интервальная оценка индивидуального значения зависимой переменной регрессионной модели.
Для определения границ доверительного интервала для отдельных (индивидуальных) значений зависимой переменной (например, для номера наблюдения t = р, р>n), применяя стандартную процедуру, составляем дробь Стьюдента:
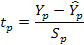
Числитель дроби представляет собой ошибку прогноза индивидуального значения эндогенной переменной
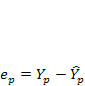
знаменатель дроби — оценка ско ошибки прогноза. Выразим дисперсию данной ошибки через выборочные данные:
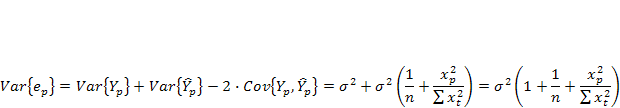
где учтено, что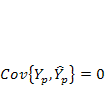 
на интервале прогнозирования. Заменяя значение дисперсии 
его оценкой, получим выражение для оценки дисперсии прогноза для наблюдения t = р
|
|
|
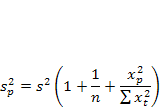
Границы доверительного интервала прогноза индивидуальных значений Yt определяются по формуле
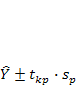
17. Алгоритм проверки адекватности регрессионной модели.
Четвертым этапом построения эконометрической модели является проверка адекватности оцененной модели. Суть: по оцененной или настроенной модели следует осуществить прогноз полученной величины и сравнить его с реальным значением этой величины, которое не использовалось на этапе настройки модели. Найдем прогнозное значение величины, затем рассчитаем истинную ошибку данного прогноза, для этого необходимо вычесть из прогнозного значения величины ее истинное значение. Если это значение меньше среднего квадратического отклонения, то модель считается адекватной. Если же большое, но неадекватной.
Процедура проверки адекватности оцененной линейной модели:
1.Вся имеющаяся в распоряжении выборка наблюдений делится на две неравные части: обучающую и контролирующую. Обучающая выборка включает основную (большую) часть наблюдений. Контролирующая выборка содержит до 5% от общего объема выборки
2.По обучающей выборке оценивается модель (рассчитываются оценки параметров модели и их стандартные ошибки).
3.Задается значение доверительной вероятности Рдов =1-α и определяется критическое значение дроби Стьюдента tкрит
4.Проверить, попадают ли значения эндогенной переменной из контролирующей выборки в соответствующие доверительные интервалы. Если да, то признать оцененную модель адекватной. Если нет – то доработка модели.
Если все значения эндогенных переменных из контрольной выборки накрываются соответствующими доверительными интервалами, то полученная модель с вероятностью Рдов считается адекватной, т.е. пригодной для дальнейшего использования в целях решения экономических задач
18. Коэффициент детерминации регрессионной модели.
Коэффициент детерминации рассматривают, как правило, в качестве основного показателя, отражающего меру качества регрессионной модели, описывающей связь между зависимой и независимыми переменными модели. Коэффициент детерминации показывает, какая доля вариации объясняемой переменной y учтена в модели и обусловлена влиянием на нее факторов, включенных в модель:
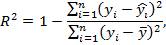
где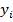 
– значения наблюдаемой переменной, 
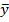– среднее значение по наблюдаемым данным, 
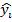– модельные значения, построенные по оцененным параметрам.
В случае, когда значение константы задается вручную, коэффициент детерминации рассчитывается по следующей формуле:
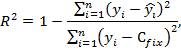
где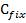 
– фиксированное значение константы. В случае линейной регрессии с константой справедлива следующая формула:
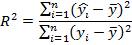
Заметим, что данная формула справедлива только для модели с константой, в общем случае используется предыдущая формула.
Чем ближе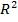 
к 1, тем выше качество модели.
При равенстве коэффициента единице линия регрессии точно соответствует всем наблюдениям.
Равенство коэффициента нулю означает, что выбранные факторы не улучшают качество предсказания 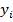по сравнению с тривиальным предсказанием 
.
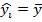Достаточно качественной можно признать модель с коэффициентом детерминации выше 0,8.
Недостатком коэффициента детерминации является то, что он увеличивается при добавлении новых объясняющих переменных, что необязательно означает улучшение качества регрессионной модели. По этой причине, для устранения этого недостатка, на практике чаще используется скорректированный коэффициент детерминации.
19. Нецентрированный коэффициент детерминации регрессионной модели.
Вариант коэффициента детерминации, который используют при оценивании регрессионной модели без константы:
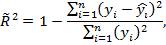
где 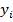– значения наблюдаемой переменной, 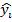– модельные значения, построенные по оцененным параметрам.
20. Скорректированный коэффициент детерминации модели множественной регрессии.
Скорректированный коэффициент детерминации позволяет учесть при оценке качества модели соотношение количества наблюдений и количества оцениваемых параметров модели.
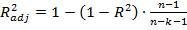
где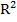 
– коэффициент детерминации, n – общее число наблюдений, k – число объясняющих переменных (число параметров модели регрессии без учета свободного члена).
Скорректированный коэффициент детерминации применяется для решения двух типов задач:
– оценка тесноты связи между объясняемой и объясняющей переменной. Необходимо обратить внимание на близость к нескорректированному коэффициенту детерминации. Модель считается качественной, если показатели велики и несильно отличаются друг от друга.
– сравнение моделей с различным числом параметров. При прочих равных условиях, предпочтение отдается той модели, у которой скорректированный коэффициент детерминации больше.
Следует отметить, что скорректированный коэффициент детерминации нельзя использовать в формулах, где применяется обычный коэффициент детерминации, поскольку скорректированный коэффициент детерминации нельзя интерпретировать как долю вариации объясняемой переменной, обусловленную вариацией факторов, включенных в модель.
21. F-тест качества спецификации регрессионной модели.
Статистикой обсуждаемого ниже критерия гипотезы H0: R2=0 (гипотеза о том что модель абсолютно плохая) против альтернативы H1: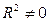 
служит случайная переменная:
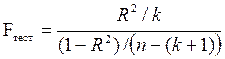(1)
Если Fтест ≤ Fкрит., то спецификация некачественная
Fтест > Fкрит., то спецификация качественная.
Здесь k — количество регрессоров в модели множественной регрессии, п — объем обучающей выборки (у, X), по которой оценена МНК-модель. В ситуации, когда гипотеза H0 справедлива, а случайный остаток и в модели обладает нормальным законом распределения, случайная переменная Fтест имеет распределение Фишера с количествами степеней свободы ν1 и ν2, где ν1=k и ν2=n-(k+1) (2)
Данное утверждение положено в основу F-теста. Вот этапы выполнения этой процедуры.
1) вычислить величину (1);
2) задаться уровнем значимости а € (0, 0,05] и при помощи
функции FPACПOБP Excel при количествах степеней свободы
(2) отыскать (1-α)-квантиль распределения Фишера Fкрит
3) проверить справедливость неравенства F<Fкрит (3)
Если оно справедливо, то принять гипотезу H0 и сделать вывод о неудовлетворительном качестве регрессии, т.е. об отсутствии какой-либо объясняющей способности регрессоров в рамках линейной модели.
Напротив, когда неравенство (3) несправедливо —следует отклонить гипотезу H0 в пользу альтернативы H1. Другими словами, сделать вывод о том, что качество регрессии удовлетворительно, т.е. регрессоры в рамках линейной модели обладают способностью объяснять значения эндогенной переменной у.
22. Спецификация множественной линейной регрессионной модели.
Суть регрессионного анализа: построение математической модели и определение ее статистической надежности.
Вид множественной линейной модели регрессионного анализа:
Y = b0 + b1xi1 + ... + bjxij + ... + bkxik + ei
где ei - случайные ошибки наблюдения, независимые между собой, имеют нулевую среднюю и дисперсию s.
Назначение множественной регрессии: анализ связи между несколькими независимыми переменными и зависимой переменной.
Экономический смысл параметров множественной регрессии
Коэффициент множественной регрессии bj показывает, на какую величину в среднем изменится результативный признак Y, если переменную Xj увеличить на единицу измерения, т. е. является нормативным коэффициентом.
Матричная запись множественной линейной модели регрессионного анализа:
Y = Xb + e
где Y - случайный вектор - столбец размерности (n x 1) наблюдаемых значений результативного признака (y1, y2,..., yn);
X - матрица размерности наблюдаемых значений аргументов;
b - вектор - столбец размерности неизвестных, подлежащих оценке параметров (коэффициентов регрессии) модели;
e - случайный вектор - столбец размерности (n x 1) ошибок наблюдений (остатков).
На практике рекомендуется, чтобы n превышало k не менее, чем в три раза.
Задачи регрессионного анализа
Основная задача регрессионного анализа заключается в нахождении по выборке объемом n оценки неизвестных коэффициентов регрессии b0, b1,..., bk. Задачи регрессионного анализа состоят в том, чтобы по имеющимся статистическим данным для переменных Xi и Y:
· получить наилучшие оценки неизвестных параметров b0, b1,..., bk;
· проверить статистические гипотезы о параметрах модели;
· проверить, достаточно ли хорошо модель согласуется со статистическими данными (адекватность модели данным наблюдений).
Построение моделей множественной регрессии состоит из следующих этапов:
1. выбор формы связи (уравнения регрессии);
2. определение параметров выбранного уравнения;
3. анализ качества уравнения и поверка адекватности уравнения эмпирическим данным, совершенствование уравнения.
Множественная регрессия:
· Множественная регрессия с одной переменной
· Множественная регрессия с двумя переменными
· Множественная регрессия с тремя переменными
23. Оценка параметров множественной регрессионной модели методом наименьших квадратов.
Множественная регрессия позволяет построить и проверить модель линейной связи между зависимой (эндогенной) и несколькими независимыми (экзогенными) переменными: y = f(x1,...,xр), где у - зависимая переменная (результативный признак); х1,...,хр - независимые переменные (факторы).
Линейное уравнение множественной корреляции: y=a+b1x1+b2x2+…+bpxp+ε. Для оценки параметров уравнения множественной регрессии применяют МНК. Для линейных уравнений и нелинейных уравнений, приводимых к линейным, строится следующая система нормальных уравнений, решение которой позволяет получить оценки параметров регрессии:
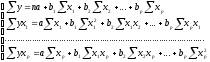
Для ее решения может быть применён метод определителей: a=∆a / ∆, b1=∆b1 / ∆,…, bp=∆bp / ∆, - определитель системы
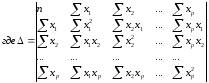
∆a, ∆b1,…, ∆bp – частные определители; которые получаются путем замены соответствующего столбца матрицы определителя системы данными левой части системы.
24. Основные числовые характеристики вектора оценок параметров классической множественной регрессионной модели.
1) Вектор математических ожиданий
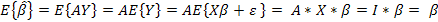
МНК-оценки параметров множественной регрессии несмещенные
2) автоковариационная матрица вектора оценок параметров
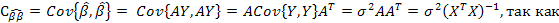
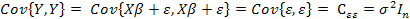
Дата добавления: 2018-08-06; просмотров: 1836; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!